Глава8.

Динамический мезоскопический конденсатор

Такой элемент электрической цепи как конденсатор не пропускает постоянный электрический ток,поскольку каждая обкладка кон денсатора соединена только с одним полюсом источника питания.Нас будет интересовать ситуация,когда обкладка конденсатора настолько мала , что начина - ет играть существенную роль плотность состояний электронов в ней . Ко - нечность плотности состояний влияет на связь между зарядом и потен - циалом обкладки,то есть,влияет на емкость конденсатора.П одчеркнем, что емкость оказывается зависящей не только от геометрических размеров, как для обычного макроскопического конденсатора,но также и от свойств электронной системы образца.Фактически,геометрическая емкость оказывается последовательно включенной с емкостью,определя емой плотностью состояний.Такой конденсатор мы будем называть мезоскопическим конденсатором [115].В качестве второй обкладки может использоваться другой мезоскопический образец,не имеющий прямого элек трического контакта с рассматриваемым мезоскопическим образцом.Одн ако зачастую просто используется макроскопический металлический электрод(затвор). Поэтому,не ограничивая общности мы будем называть мезоско пическим конденсатором собственно мезоскопический образец,соеди ненный с одним резервуаром электронов.

Изменяя периодически во времени потенциал либо резервуара либо затвора(либо оба одновременно)можно вызвать изменяющийс я во време - ни поток электронов между мезоскопическим конденсатором и резервуаром,текущий то в одну,то в другую сторону. 1 Свойства этого потока частиц и представляет предмет нижеследующего рассмотрения В силу калибро-

1Фактически переменный ток течет от резервуара через мезоскопический образец к затвору.Цепь замыкает источник питания,создающего разность потенциалов между элек тронным резервуаром и затвором.Для простоты рассмотрения мы будем полагать,что геометрическая емк ость,определяющая разность потенциалов между мезоскопическим образцом и затвором,намного превосходи т вклад от плотности состояний.Поэтому, суммарная емкость определяется исключительно последним вкладом и потенциал мезоскопического образца совпадает с потенциалом затвора.

221

8.Динамический мезоскопический конденсатор

вочной инвариантности ток должен зависеть только от разности потенциалов резервуара и затвора и не должен зависеть от каждого из потенциалов по-отдельности.Поэтому,мы рассмотрим случай(если не ого ворено иное), когда изменяется потенциал затвора,а потенциал резервуар а фиксирован . Электроны в резервуаре находятся в равновесном состоянии и описываются фермиевской функцией распределения f0(E) с химическим потенциалом µ0 и температурой kBT0.

8.1.Общая теория для одноканального рассеивателя

Положим,что проводник,соединяющий мезоскопический обра зец с резервуаром,является одномерным.Кроме того,будем счита ть,что рассеяние не зависит от спина и,поэтому,будем считать электроны б есспиновыми. В таком случае образец представляет собой рассеиватель , имеющий всего один орбитальный канал рассеяния,один входящий и один ис ходящий. Такой рассеиватель мы будем называть одноканальным рассеивателем (1КР).В стационарном случае1КР характеризуется всего одн ой амплитудой рассеяния S = eiφ, описывающей полное отражение налетающего элек - трона от рассеивателя, φ – изменение фазы волновой функции при отражении.Однако,если под действием потенциала затвора,потенц иал образца периодически изменяется во времени,то упомянутая амплиту да рассеяния становится матрицей в пространстве энергии с элементами SF (En, E), где En = E + n!Ω0 и n – целое.Мы будем называть эту матрицу матрицей рассеяния Флоке.

8.1.1.Амплитуды рассеяния

В случае динамического 1 КР матрица рассеяния Флоке может быть выражена через одну амплитуду рассеяния в смешанном представлении, либо через амплитуду Sin(t, E) либо через амплитуду Sout(E, t),

T	dt
SF (E + n!Ω0, E) = Sin,n(E) ≡ ˆ
		einΩ0tSin(t, E) ,	(8.1)
	T
0

222

8.1.Общая теория для одноканального рассеивателя

						T		dt
SF (E, E − n!Ω0) = Sout,n(E) ≡ ˆ
									einΩ0tSout(E, t) ,	(8.2)
								T
				0
где T = 2π/Ω0 – период изменения потенциала на затворе.
Из определения следует такое соотношение между амплитудами,
	Sin, n(E) = Sout, n(En) ,									(8.3)
которое во временном´ представлении есть,
		∞	T
Sin(t, E)	=	!	ˆ	T) einΩ0		(t	−t) Sout(En, t)) ,
				dt		!
		n=−∞ 0								(8.4)
		∞	T
Sout(E, t)	=	!	ˆ	T) einΩ0		(t	−t) Sin(t), E−n) .
				dt		!

n=−∞ 0

8.1.2.Условия унитарности

Условие унитарности гласит,

∞	∞
!	!
SF (En, Em) SF (En, E) =	SF (Em, En)SF (E, En) = δm,0 . (8.5)
n=−∞	n=−∞

Используя уравнения( 8.1) и (8.2) мы получим из уравнения (8.5) следую - щие условия унитарности для Sin и Sout, см . (3.60) :

T	dt			T	dt
ˆ				ˆ
		eimΩ0t Sin(t, Em) Sin(t, E)	=			eimΩ0t Sout(Em, t) Sout	(E, t)
	T				T
0				0
			= δm,0 .				(8.6)

223

8.Динамический мезоскопический конденсатор

Далее,используя вторые из равенств в( 8.5) и (8.6),получим,

∞	∞
!	!
e−imΩ0t	SF (Em, En) SF (E, En) =
m=−∞	n=−∞	(8.7)
∞
		∞
= m=−∞ e−imΩ0t )Sout(Em, t) Sout(E, t)*m		= m=−∞ e−imΩ0t δm,0 = 1 .
!		!

Фактически,мы доказали следующее соотношение,являющеес я следстви - ем унитарности,для1КР,

!∞ ˆT dtT) e−inΩ0(t−t!) Sin(t, En) Sin(t), En) = 1 ,

n=−∞ 0

или равноценно,

!∞

e−inΩ0t Sin(t, En) Sout, −n(E) = 1 ,

n=−∞

!∞ !∞

e−imΩ0t Sout, n+m(Em) Sout, n(E) = 1 ,

m=−∞ n=−∞

!∞ !∞

e−imΩ0t Sin, n+m(E−n) Sin, n(E−n) = 1 .

m=−∞ n=−∞

8.1.3.Зависящий от времени ток

(8.8)

(8.9a)

(8.9b)

(8.9c)

Общее выражение для зависящего от времени тока в случае одного орбитального канала рассеяния есть: [35]

224

8.1.Общая теория для одноканального рассеивателя

I(t) = e		ˆ dE	∞	f0(E) f0(En)	∞	e−ilΩ0t SF	(En, E) SF (En+l, E),
			!		!
	h	n=−∞<		−	=l=−∞

(8.10)

Это выражение может быть значительно упрощено.Для этого мы делаем замену E → En в той части , которая зависит отf0(En), и из тождества (8.7) находим,что вся эта часть сводится к f0(E). Тогда , используя определение (8.1) в оставшейся части выражения (8.10),мы получаем, [ 116]

		h		<@			@ −		=	(8.11)
I(t) = e ˆ				dEf0(E)			Sin(t, E) 2		1 .
						@	@
Легко показать,что в адиабатическом режиме ток выражается										через ква-
зистационарную амплитуду рассеяния,							.S(t, E) ∂S ∂t .
I(t) = − 2π ˆ				dE -− ∂E0						(8.12)
	ie				∂f				(t, E)

в соответствие с общей теорией развитой в [34] ( смотри , например 72, []). Для этого мы используем следующее разложение,справедливо е в первом порядке по Ω0 для амплитуды рассеяния1КР в адиабатическом режиме,

	Sin(t, E) = S(t, E) +		i! ∂2S(t, E)				,	(8.13)
			2 ∂t∂E
	где S – квазистационарная	амплитуда рассеяния. 2						При вычислении
	|Sin(t, E)|2 мы учтем,что |S|2	= 1 и,соответственно,					∂2|S|2/(∂t∂E) = 0.

Кроме того,мы используем следующее,

2Смотри первые два слагаемых(линейных по частоте Ω0)в правой части выражения( 8.62) для 1 КР , вклю - чающего единичный источник.Обратим внимание на тот факт,чт о в случае 1 КР , включающего два источни - ка,соединенных последовательно,аномальная амплитуда расс еяния A отлична от нуля,смотри выражение (9.39).Однако это не изменяет выражение для тока( 8.12).

225

8.Динамический мезоскопический конденсатор

∂S ∂S

=

∂S

SS

∂S

= S

∂S

∂S

S =

∂S ∂S

,

∂t ∂E

∂t

∂E

∂t ∂E

∂t ∂E

и получим ( с точностью до членов Ω0):

|Sin(t, E)|2 ≈ 1 − i! ∂ -S ∂S ..

∂E ∂t

Подставляя это выражение в( 8.11) и интегрируя по частям по энергии , мы приходим к выражению( 8.12).

8.1.4.Поток тепла

В отличие от электрического тока , тепловой поток , уносимыйэлектронами от динамического1КР в резервуар,не обнуляется при уср еднении по времени.Его постоянная составляющая выражается следующи м образом через элементы матрицы рассеяния Флоке,

∞

dE ∞

(En

µ0) [f0(E)

f0(En)] SF (En, E) 2 . (8.14)

IE = 1 ˆ

!

−

−

|

|

h

n=−∞

0

Подставляя сюда тождество( 8.5) с m = 0 и заменяя En

→ E в части с

f0(En) мы получим,

∞

∞

n SF (En, E) 2 +

IE = Ω0 ˆ dE f0(E)

!

|

|

2π

n=−∞

0

∞

∞

SF (En, E) 2

+ 1 ˆ dE (E µ0) f0(E)

−

!

|

| −

h

n=−∞

0

∞

∞

SF (E, E−n) 2 =

1 ˆ dE (E µ0) f0(E)

−

−

!

|

|

h

0

n=−∞

226

8.1.Общая теория для одноканального рассеивателя

∞

(E) ∞ n SF (En, E) 2 .

= Ω0 ˆ dE f0

!

2π

|

|

0

n=−∞

Затем

переходя

к

амплитуде

рассеяния Sin,n(E)

=

SF (En, E) и ис -

пользуя

следующее свойство

коэффициентов Фурье,

Ω0nSin,n

(E) =

−

i

{

∂S

(t, E)/∂t

}−n

, мы окончательно получим : [116]

in

i

∞

T

∂S

in

(t, E)

IE

=

ˆ dE f0(E) ˆ

dt

(8.15)

Sin(t, E)

.

T

∂t

− 2π

0

0

Заметим выражения( 8.11) и (8.15) являются справедливыми при про - извольной частоте и амплитуде осциллирующего потенциала. Недостатком же их является то,что они требуют вычисления амплитуды расс еяния для энергий всех состояний,плотностью или частично заполненн ых электронами в резервуаре.

8.1.5.Тепловой поток и квадрат тока

Как оказывается в адиабатическом режиме( Ω0 → 0) при нулевой тем - пературе тепловой поток IE, генерируемый динамическим 1 КР , простым об - разом связан с усредненным по времени квадратом тока, 0I21. Из выраже - ние( 8.12) мы находим при нулевой температуре ,

ie

I(t) = − 2π S(t, µ0)

∂S (t, µ0)	.	(8.16)
∂t

Используя тождество, SdS = −dS S , следующее из условия унитарности для квази-стационарной амплитуды рассеяния, |S(t, E)|2 = 1, мы предста - вим квадрат тока в следующем виде,

2

S ∂t

∂t

2

∂t ∂t

2

@

@

2

I2(t) = − 4eπ2

S

= 4eπ2 S S

= 4eπ2

∂t

,

@

@

∂S

∂S

∂S ∂S

∂S

@

@

@

@

227

8.Динамический мезоскопический конденсатор

и запишем его среднее как

T

dt

e2Ω2

∞

<|

ˆ

0

!

2 + S−n

2

I2

1

=

T

I2(t) =

2

n2

Sn

|

|

.

(8.17)

0

0

4π

n=1

|

=

Чтобы вычислить тепловой поток IE в адиабатическом режиме мы используем выражение( 8.14),в котором разложим: f0(En) ≈ f0(E) +

n!Ω0 ∂f0(E)/∂E + (n2!2Ω20/2) ∂2f0(E)/∂E2. Кроме того , для амплитуды рассеяния SF (En, E) = Sin,n(E) мы используем разложение( 8.13).Тогда

с точностью до членов порядка Ω20 находим,

Ω0

∞

∂f0(E)

IE =

ˆ

dE (E − µ0) -−

.

2π

∂E

0

!Ω2

∞

∞

∂f0(E)

!

+

0

ˆ dE -−

. n=

4π

∂E

−∞

0

!∞

n |Sn(E)|2

n=−∞

n2 |Sn(E)|2 .

Первое слагаемое тождественно равно нулю для1КР.Для того, чтобы показать это мы используем тот факт,что квазистационарная ам плитуда рассеяния может быть записана так,

S(t, E) = eiφ(t,E) ,

(8.18)

где фаза периодична по времени, φ(t, E) = φ(t + T, E). Поэтому , получим

∞

T

dt

∂S (t, E)

T

dt ∂φ(t, E)

!

Sn(E) 2

= ˆ

T S(t, E)

=

i ˆ

T

= 0 .

inΩ0

n=−∞

|

|

0

∂t

−

0

∂t

Следовательно,тепловой поток,генерируемый динамически м 1 КР , равен

228

8.2.Емкость кирального одномерного кольца

	!Ω2	∞		∂f (E)		!	<	=
		0
						∞
IE =	0	ˆ	dE -−	0		. n=1 n2	|Sn(E)|2 + |S−n(E)|2	. (8.19)
	4π			∂E

Сравнивая выражения( 8.17) и (8.19) мы заключаем , что при нулевой тем - пературе[ 116]

IE = Rq 0I21,

(8.20)

где Rq = h/(2e2) – универсальное сопротивление,которое не зависит от свойств1КР и называется квантом релаксационного сопротивления

(charge relaxation resistance quantum) [115].Это сопротивление ответствен-

но за динамику релаксации заряда рассеивателя.

8.2.Емкость кирального одномерного кольца

В двумерном электронном газе в сильном магнитном поле реализуется режим целочисленного квантового эффекта Холла[ 118].Благодаря закручиванию траекторий в магнитном поле,электроны в масс иве оказываются локализованными.И только вдоль границы(двумерног о)образца существуют так называемые краевые состояния, в которых электро - ны движутся без рассеяния(баллистически)в одном направле нии[ 119]. Если локализовать(с помощью потенциальных барьеров)малу ю область , квантовую точку,то в сильном магнитном поле электроны буду т двигаться вдоль края этой точки по замкнутым траекториям,круговым кр аевым состояниям.Квантование движения вдоль таких траекторий при водит к дискретному спектру с однократным заполнением,что соответст вует эффективно бесспиновым киральным частицам.Экспериментально б ыло показано[ 117, 120],что такая квантовая точка,потенциал которой периодически изменяется со временем,является эффективным и хорошо у правляемым источником потока единичных электронов и дырок,работа ющим в гигагерцовом диапазоне.Для этого квантовая точка должны быт ь соедине -

229

8.Динамический мезоскопический конденсатор

на с линейным краевым состоянием,выполняющим роль проводн ика 3, по которому движутся электроны.Роль соединительного элемен та выполняет квантовый точечный контакт с регулируемой вероятностью прохождения. Таким образом,используя круговые краевые состояния,как р егулируемые источники частиц(РИЧ),линейные краевые состояния – как волноводы, и квантовые точечные контакты – как разветвлители потока частиц 4, по - является возможность создания суб-наносекундных квантовых электронных устройств.Теоретически были рассмотрены простейшие ц епи,включающие РИЧ и предсказано следующее: (а)эффект квантования др обового шума[ 121], (б)для двух,соединенных последовательно РИЧ,предсказ а- но существование режимов двух-частичной эмиссии и реабсорбции[ 44],а также(в)предсказано возникновение корреляций между част ицами,эмитированными двумя независимыми РИЧ,проявляющимися как регу лируемый двух-частичный эффект Ааронова-Бома[ 122].Частотно-зависимый шум, создаваемый РИЧ,экспериментально[ 123] изучался в неадиабатическом режиме(скачкообразное изменение потенциала во времени)и теоретически [116] изучался в адиабатическом режиме ( плавное изменение потенциала во времени).Используя концептуально простую модель РИЧ(раб отаюшего в неадиабатическом режиме),предложенную в работе[ 123],авторы работы [124] вычислили спектр шума , а также определили генерирующую функцию,позволяющую вычислить корреляционные функции тока бо лее высокого порядка.

8.2.1.Модель и амплитуда рассеяния

Мы рассмотрим модель одноканального рассеивателя[ 125, 117, 120, 126],которая включает единичное круговое состояние длиной L, киральное одномерное кольцо,соединенное с помощью квантового точеч ного контакта (КТК)с одномерным киральным проводником,по которому расп ространяются электроны,выходящие из резервуара с температурой T0 и фермиев - ской энергией µ0, смотри рис .8.1. В силу киральности ( однонаправленно - сти)движения,характеристики резервуара,предполагаемо го быть справа

3Аналог волновода в оптике

4Аналог полупрозрачного зеркала в оптике

230

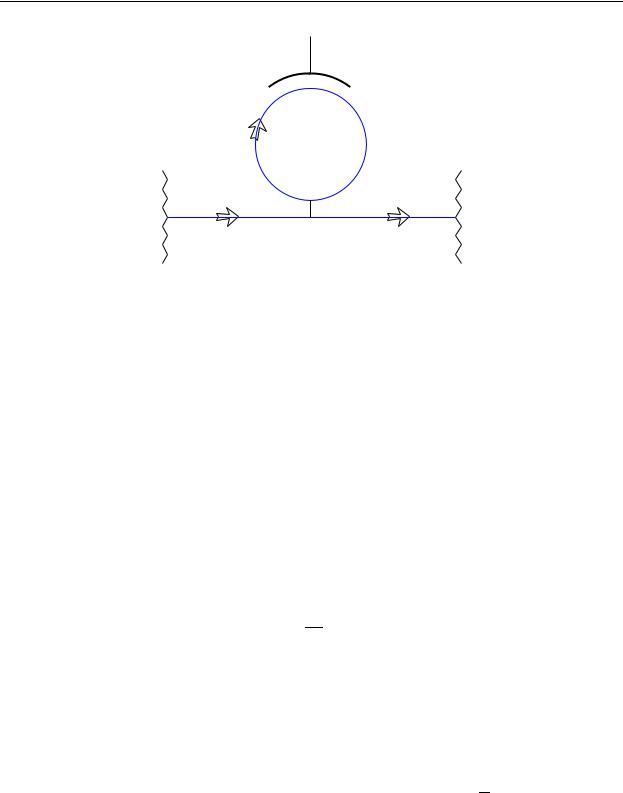
8.2.Емкость кирального одномерного кольца

U(t)

Рис. 8.1.Одноканальный рассеиватель в виде кирального одн омерного кольца с периодическим по времени потенциалом U(t), создаваемым метал - лическим затвором.Штриховая линия изображает квантовый т очечный контакт,соединяющий круговое и линейное краевые состояния.С трелки показывают направление движения электронов.Электронные резе рвуары обозначены волнистыми линиями.

на рисунке,в который попадают электроны из линейного краев ого состояния,несущественны.Однородно вдоль периметра кольца наве ден периодический во времени потенциал U(t) = U(t + T).

Используя метод,аналогичный изложенному в разделе 3.5.3, мы полу - чим нижеследующее выражение для матрицы рассеяния Флоке динамического кирального одномерного кольца:

T	dt
SF (En, E) = ˆ
	T einΩ0t Sin(t, E) ,	(8.21a)

		0
		∞
		!q
Sin(t, E)	=	eiqkLS(q)(t) ,
		=0
S(0)	=	r , S(q>0)(t) = t¯2 rq−1 e−iΦq(t) ,

(8.21b)

t

Φq(t) = !e ˆ dt)U(t)) ,

t−qτ

231

8.Динамический мезоскопический конденсатор

где r(E)/t¯(E) – амплитуда отражения/прохождения для КТК,соединяющего кольцо с линейным краевым состоянием, τ = meL/(!k) – время однократного прохождения вдоль кольца для электрона с энергией E. Матри - ца рассеяния в смешанном представлении Sin(t, E) представлена как сумма амплитуд,соответствующих электрону с энергией E протуннелировавшему в кольцо и затем покинувшему его в момент времени t. Индекс q показывает сколько раз электрон обошел кольцо до того,как покинул его п ротуннелировав через КТК.Вышеприведенное выражение получено в сл едующих предположениях.Во-первых,квант энергии !Ω0 намного меньше энергии

электрона, !Ω0 - E. И , во - вторых , амплитуда отражения / прохождения для КТК изменяется существенно в масштабе энергий δE E, который на - много превосходит !Ω0. Поэтому , мы пренебрегли членами порядка!Ω0/δE

и меньше .

Получим выражения( 8.21).Для того,чтобы вычислить SF (En, E) мы рассмотрим рассеяние плоской волны e−iEt/!+ikx с единичной амплитудой и энергией E, распространяющейся в одномерном проводнике , как показа - но на рис. 8.1, на динамическом 1 КР , роль которого выполняет последова - тельно соединенные кольцо и точечный контакт.Введем ось x вдоль одномерного проводника и ось y вдоль периметра кольца.Квантовый точечный контакт соединяет точки x = 0 и y = 0. Тогда волновая функция может быть представлена в следующем виде:

Ψ(t, x) = e−iEt/!+ikx ,								x < 0 ,	(8.22a)
		"
				k
	iEt/!	∞					inΩ0t+iknx
e−		n=−∞ Skn				SF (En, E) e−		, x > 0 ,

∞		∞
!		!
Ψ(t, y) = e−iEt/!	e−inΩ0t	alΥn−leikly , 0 < y < L ,	(8.22b)
n=−∞		l=−∞

где Υp – коэффициент Фурье для Υ(t), которая зависит от однородного по - тенциала U(t), приложенного к кольцу , следующим образом ,

232

8.2.Емкость кирального одномерного кольца

			ie	t	dt)U(t)) .
	Υ(t) = exp			ˆ		(8.23)
			!
		−		−∞

Ниже мы будем полагать,что

, = !EΩ0 - 1 . (8.24)

Тогда в нулевом порядке по , мы получаем[в случае,когда пространственные координаты ограничены такими условиями: x, y - L/(,Ω0τ)]:

kn	≈ 1, eiknx ≈ eikxeinΩ0x/v ,	(8.25)
k

где v = !k/me – скорость электрона с энергией E.

Для сокращения записи введем следующие периодические во времени функции:

∞		∞
!		!
Sin(t, E) =	e−inΩ0tSF (En, E) , a(t) =	e−ilΩ0t al .	(8.26)
n=−∞		l=−∞

Подставляя их в выражение( 8.22) и выполняя обратное преобразование Фурье,получим

Ψ(t, x) =	e−iEt/!+ikx ,								x < 0	,	(8.27a)
		) − v					*
					x
	Sin		t			, E		e−iEt/!+ikx , x > 0		,
			y					iEt/!+iky
Ψ(t, y) = a )t −				*Υ(t) e−					, 0 < y < L .		(8.27b)
			v

Используя матрицу рассеяния для точечного квантового контакта,

233

8.Динамический мезоскопический конденсатор

можно сформулировать граничное условие,связывающее межд у собой ам - плитуды волновой функции при x = 0 и y = 0. Положим , что элементы матрицы рассеяния КТК r и t¯ не зависят от энергии на масштабе энергий порядка !Ω0. Тогда различные члены в (8.22) ( соответствующие различным энергиям)будут иметь одинаковые граничные условия при x = 0 и y = 0. Поэтому,можно использовать такие же граничные условия непосредственно для волновой функции,записанной в( 8.27):

Sin(t, E)	.	¯	1	.,
		r(E) t(E)
- a(t)Υ(t)		= - t¯(E) r(E)	.- a(t − τ)Υ(t) eikL		(8.28)

где τ = L/v – время одного оборота,которое было введено после выраже-

ния( 8.21).

Решим систему уравнений( 8.28) методом последовательных прибли - жений и учтем все порядки теории возмущений.Уравнение для a(t),

a(t)Υ(t) = t¯+ r a(t − τ) Υ (t) eikL ,

имеет такое решение:

		∞
¯	¯	!q
		q iqkL		(t − qτ) .	(8.29)
a(t) = t Υ	(t) + t	r e	Υ
		=1

Подставляя выражение( 8.29) в первое уравнение системы (8.28),получим

	∞
¯2	!q	q−1	iqkL			(8.30)
Sin(t, E) = r + t Υ(t)	r		e	Υ	(t − qτ) .
	=1

Затем используя выражение( 8.23) мы приходим к анонсированному ранее решению( 8.21b).

8.2.2.Унитарность

Условие унитарности( 8.6) для Sin есть( m = 0) :

234

8.2.Емкость кирального одномерного кольца

T

ˆ

dt

|Sin(t, E)|2 = 1 .

(8.31)

T

0

Покажем,что матрица рассеяния,определяемая выражением(

8.21b),удо-

влетворяет этому условию.Для этого запишем,

T

ˆ

dt

|Sin(t, E)|2 = A + B ,

T

0

T

2 ∞

!q

A = R +

Rq = R + T = 1 ,

R

=1

T

dt

8

∞

B

=

0

2 :

!q

T

ˆ

− T rq ei{qkL−Φq(t)} +

=1

T 2

∞

∞

rq eiqkL ei{Φm(t)−Φm+q(t)}9

!

!q

+

R

m=1 Rm

=1

=

∞

T

dt

T ∞

9

!q

0

!

= 2 T : =1

rq eiqkL ˆ

T

8R m=1 Rm e−iΦq(t−mτ) − e−iΦq(t)

= 0 ,

¯

2

2

где T = |t|

и R = |r| – вероятности прохождения и отражения.В послед-

ней строке мы учли следующее равенство Φm+q(t) − Φm(t) = Φq(t − mτ). Кроме того,использую периодичность Φq(t), мы выполнили сдвиг t −mτ → t в подинтегральном выражении по времени .

Заметим,что в стационарном случае,когда Υ(t) = 1, элементы мат - рицы рассеяния Флоке SF (En, E) = δn,0 S(E), где стационарная амплитуда рассеяния есть,

235

8.Динамический мезоскопический конденсатор

t¯2 eikL

S(E) = r + 1 − r eikL .

Эта величина может быть также переписана с таком виде,

r − R e−ikL

S(E) = −eikL (r − R e−ikL) ,

который подчеркивает ее унитарность.

8.2.3.Калибровочная инвариантность модели

(8.33a)

(8.33b)

Покажем,что используемая нами модель удовлетворяет услов ию калибровочной инвариантности,то есть,величина тока не зави сит от того приложен ли потенциал U(t) к резервуару , либо же потенциал−U(t) приложен к затвору .

Для этого мы вычислим ток,предположив,что периодический п отенциал U(t) = U(t+2π/Ω0) приложен к резервуару,в то время как рассеиватель остается стационарным.В этом случае состояние электрона в резервуаре описывается волновой функцией Флоке,смотри выражения( 3.27), (5.18). Итак,пусть оператор aˆ)†(E) рождает электрон в состоянии,описываемом следующей волновой функцией,

. E	∞
ΨE(t,0r) = eik.re−i ! t	!
	Υn e−inΩt ,	(8.34)

n=−∞

где Υn – Фурье коэффициент для функции Υ(t), определенной в выраже -

нии( 8.23).В случае если U(t) = U cos(Ωt), то Υn = Jn (eU/!Ω), гле Jn – функция Бесселя первого рода n−го порядка.Операторы рождения и уни-

чтожения aˆ)†(E) и aˆ)(E) описывают равновесные электроны с фермиевской функцией распределения,

0aˆ)†(E), ˆa)(E))1 = δ(E − E))f0(E) .

(8.35)

236

8.2.Емкость кирального одномерного кольца

Мы предположим,что в проводнике,соединяющем рассеивател ь с ре - зервуаром потенциал равен нулю.Поэтому,волновой функцие й электрона с энергией E в проводнике является плоская волна ,ψE(t, x) = eikx−iE! t. На -

помним,что волновое число		0
	k в ψE(t, x) и k в ΨE(t,0r) зависят от энергии
по-разному.Если в проводнике k =		2meE/!2	зависит от энергии E элек-
трона,то в резервуаре модуль	волнового вектора				зависит от энергии Фло-
	5			k
ке E и одинаков для всех компонентов волновой функции , соответствующих
различным энергиям En − E	= n!Ω,	n = 0 , ±1 , ±2 . . . . Пусть оператор

aˆ†(E) рождает электрон с энергией E в проводнике . Тогда , учитывая вкла - ды от всех состояний в резервуаре,у которых есть компонента с энергией E, смотри выражение (5.24),выразим оператор aˆ(E) через операторы уничтожения электронов в резервуаре,

!∞

aˆ(E) =	Υn aˆ)(E−n) .	(8.36)
	n=−∞
Напомним,что мы пренебрегаем отражением,обусловленным и		зменением

длины волны электрона,изменением величины k. Поскольку соответству - ющий коэффициент отражения по порядку величины равен (!Ω/µ0)2 - 1, а мы , как правило , пренебрегаем такого рода величинами при ычислениив матрицы(амплитуды)рассеяния.

После прохождения через стационарный1КР,волновая функци я элек -

		ˆ
трона умножается на амплитуду рассеяния S(E). Поэтому , операторb(E),
уничтожающий рассеянный электрон с энергией E, может быть записан
следующим образом,
	∞
ˆb(E) = S(E)ˆa(E) =	!
	S(E)Υnaˆ)(E−n) .	(8.37)

n=−∞

Далее мы вычислим ток I(t) в одномерном проводнике , обусловленный наличием рассеивателя.Этот ток определим как разность ток ов в проводнике после и до рассеивателя, 5

5Если параметры обоих резервуаров,к которым присоединен провод ник,одинаковы,то ток I(t) может быть

237

8.Динамический мезоскопический конденсатор

e

∞

I(t) =

¨ dEdE) eiE−!E! t

ˆb†(E)ˆb(E))

aˆ†(E)ˆa(E))

.

h

0

<0

1 − 0

1=

Вычислим l−ю гармонику тока :

e

T

dt

∞

ˆ

¨

E−E!

ˆb†(E)ˆb(E))

Il =

eilΩ0t

dEdE) ei

!

t

1 − 0

aˆ†(E)ˆa(E))

.

h

T

0

0

<0

1=

(8.38)

(8.39)

Используя выражения( 8.35) - (8.37) и выполняя сдвиг E → E + n!Ω под знаком интегрирования по энергии,мы окончательно получим ,

		∞		∞
	e	ˆ		!
Il =			dEf0(E)	Υn/ Υn+l	S/(En) S(En+l)	−	1	.	(8.40)
	h	0		n=−∞	<			=

Для того,чтобы упростить полученное выражение,мы введем т акую периодическую функцию,

!∞

S(t, E) =

S(En) Υn e−inΩt ,

(8.41)

n=−∞

и учтем , что

∞

Υ/ Υn+l = δl,0. Тогда выполнив обратное преобразова -

n=−∞

n

выражении(

8.40),мы вычислим зависящий от времени ток:

ние Фурье в "

h

dEf0(E)

<@

@

−

1

=

(8.42)

I(t) = e ˆ

@

S(t, E) 2

.

@

Покажем,что полученное выражение определяет в точности та кой же ток,

измерен как ток того резервуара,в который втекают электрон ы после рассеяния

238

8.2.Емкость кирального одномерного кольца

как и выражение( 8.11) в том случае , когда потенциал−U(t) приложен к затвору.Для этого необходимо показать,что функция S(t, E) отличается от функции Sin(t, E) (8.21b),во-первых,фазовым фактором(фактически это –

Υ(t)),который не влияет на ток и,во-вторых,заменой

U → −U. Перепишем

выражение( 8.33a),

∞

!q

S(0) = r ,

S(q>0)(t) = t¯2 rq−1 ,

S(E) =

eiqkLS(q) ,

=0

и подставим его (8.41).После этого вычислим,

∞

S(t, E) =

!q

eiqkLS)(q)(t) ,

(8.43)

=0

S)(0)(t) = Υ (t) r ,

)(q>0)

¯2

q−1

!

−inΩt

˜

S

(t) = t r

e

Υn e

n

¯2

q−1

¯2

q−1 −iΦq(t)

,

= t r

Υ(t − qτ) = Υ t() t r

e

e

t

) −

Φ˜ q(t) =

ˆ

dt)

U(t)) ,

!

t−qτ

*

При вычислении этих выражений мы использовали k(En) ≈ k(E) + nΩ/v и L/v = τ ≡ h/ , где – расстояние между уровнями энергии в изолированном кольце вблизи энергии Ферми.Сравнивая выражения (8.21b) и (8.43) мы видим , что

S+U(t), E, = Υ (t) Sin+ − U(t), E,.

(8.44)

Заметим,что в функции Sin(t, E) число оборотов q в кольце определяет

239

8.Динамический мезоскопический конденсатор

набег фазы в потенциале −U(t). Это понятно , поскольку находясь в коль - це электрон подвержен действию этого потенциала.В то же вре мя,функция S(t, E) также содержит фазовые множители,в которых число оборотов в кольце связано уже с потенциалом в резервуаре U(t). Для того , чтобы пояснить полученное соотношение мы заметим следующее.Эле ктрон,который покидает резервуар в момент времени t имеет фазовый множитель Υ(t), обусловленный осциллирующим потенциалом U(t). Однако , для того , чтобы вычислить ток I(t), необходимо учесть частицы , оказавшиеся к это - му моменту времени за рассеивателем.При этом,если электро н,сделавший q оборотов,покинул кольцо в момент времени t, то такой электрон должен был покинуть резервуар в момент времени t − qτ. 6 Такой электрон имеет фазовый множитель Υ(t − qτ). Далее , если вынести в качестве общего множителя Υ(t), фазовый множитель для частичной амплитуды с q = 0, то тогда фазовый множитель для частичной амплитуды с q > 0 станет равным Υ/(t)Υ(t − qτ). Это в точности фазовый множитель , соответствующий ча - стице,вышедшей из стационарного резервуара и совершившей q оборотов в кольце с зависящим от времени потенциалом −U(t), смотри (8.21b).

8.2.4.Зависящий от времени ток

Заменяя в выражении( 8.10) элементы матрицы рассеяния Флоке на Фурье коэффициенты амплитуды рассеяния Sin(t, E) мы получим[сравни с выражением( 3.133)]:

		∞	∞			T
I(t) = e ˆ			!		f0(E) f0(En)	ˆ	T)	einΩ0	(t−t	)Sin(t, E) Sin(t), E) .
			dE
				{	−	}	dt		!
	h		n=−∞
0						0				(8.45)

Затем используем представление( 8.21b) и предположим , что масштаб энергий δE, на котором изменяется амплитуда отражения / прохождения для квантового точечного контакта,много больше,чем интер вал энергий

6Мы пренебрегаем временем движения от резервуара к месту присоединения кольца к проводнику

240

8.2.Емкость кирального одномерного кольца

max (!Ω0, kBT0) по которому выполняется интегрирование.Поэтому,величины r и t¯можно считать постоянными и вычислить их значение при E = µ0. Сделанные упрощения позволяют проинтегрировать по энергии.Для этого воспользуемся значением следующего интеграла,

∞					η -2π2s	kBT0	.,
ˆ	dEf0(E) ei2π	E−µ0	s = −i					(8.46)
				2πs
0

где η(x) = x/ sinh(x). Интегрируя по энергии член с f0(En) в Eq. (8.45),мы выполним сдвиг En → E и после этого разложим фазовый множитель в соответствие с выражениемEq. ( 8.25):

eiqknL ≈ eiqkL einΩ0τ ,

где kn = k (En). При перемножении амплитуд Sin и Sin получается двойная сумма,которую представим следующим образом:

∞ ∞	∞	∞	∞	∞	∞
! !	!	!q	!	!!
	AqBp = AqBq +			AqBq+s +	Ap+sBp .
q=1 p=1	q=1	=1 s=1		p=1 s=1

После этого полученное выражение для тока удобно представить как сумму двух слагаемых I(d) и I(nd): [126]

I(t) = I(d)(t)

I(d)(t) =

e2

T 2

∞

Rq−1

h

!q

=1

8

+

,>

?

s=1

s

2

∞

T0

ikF L

I(nd) =

eT

8

!

η

s

T

r e

πτ

s

где kF = √2meµ0/!, kBT = !/(πτ) =

+ I(nd)(t) ,				(8.47a)
{U(t) − U(t − qτ)} ,				(8.47b)
!		)	e−iΦs(t−qτ) − e−iΦs(t)		9,
∞	Rq−1
q=1				*
				(8.47c)

/(2π2). В выражении (8.47) время

241

8.Динамический мезоскопический конденсатор

одного оборота в кольце τ вычисляется для электрона с энергией Ферми, E = µ0. Вышеприведенные выражения справедливы в нулевом порядке по малому параметру max (!Ω0, kBT0) /µ0 → 0.

Вклад в генерируемый ток I(d), который мы будем называть диагональ - ным,возникает в результате интерференции таких фотон-инд уцированных амплитуд рассеяния,которые соответствуют траекториям с о динаковой длиной[одинаковый индекс q в Eq. (8.21b)].Интерферирующие амплитуды отличаются числом квантов энергии !Ω0 поглощаемых или излучаемых электроном при движении в поле потенциала U(t). Этот линей - ный по напряжению вклад оказывается не зависящим от температуры. 7 Недиагональный вклад в ток I(nd) обусловлен интерференцией фотониндуцированных амплитуд рассеяния,соответствующих трае кториям с различающейся длиной, q1 %= q2. Эта часть тока уменьшается при увеличении температуры(при T0 ! T ).Это обусловлено тем,что фаза интерференционного члена зависит от разности длин траекторий и,если так ая разность отлична от нуля,то фаза осциллирует как функция энергии.По этому,вклад в эту часть тока от электронов с различными энергиями в пределах температурного размытия края фермиевской функции распределения будем вза -

имно компенсироваться.Итак,при высоких температурах, T			0 (	T , только
ток линеен по напряжению, I(t) ≈ I	(d)
		(t). В то время как при низких тем -

пература, T0 - T , оба вклада I(d)(t) и I(nd)(t) существенны и,поэтому,ток является нелинейной функцией от U(t).

Величина тока I(t) зависит от частоты Ω0 периодически.Период δΩ0 = 2π/τ такой зависимости определяется временем τ одного оборота электрона в кольце.Если τ = nT, следовательно Ω0 = nδΩ0, то осциллирующий потенциал U(t) = U(t + T) изменяет фазу электронов на величину кратную 2π, которой можно пренебречь . Поэтому , в таком случаеI(t) = 0. Под - черкнем,что при вычислении тока I(t) рассматриваются такие электроны, которые протуннелировали в кольцо,совершили некоторое чи сло полных оборотов и покинули кольцо.Аналогично,при следующем изме нении частоты, Ω)0 = Ω0 + nδΩ0, зависящие от времени набеги фаз изменяются на величины кратные 2π, что не изменяет ток .

7Вплоть до температур,при которых становятся существенными про цессы,нарушающие фазовую когерентность.

242

8.2.Емкость кирального одномерного кольца

При частотах отличных от этих значений,набег фазы становит ся зависящим от времени.Поэтому,в соответствие с правилом сумм Фр иделя[ 13], заряд аккумулированный в кольце также зависит от времени,ч то и вызывает появление переменного во времени тока, I(t) =% 0.

8.2.5.Высокотемпературный ток

Поскольку при T0 ( T ток I(t) ≈ I(d)(t) линеен по напряжению,то мы можем ввести зависящий от частоты кондактанс,

G(d)	=	Il(d)	,	(8.48)
l		Ul

где Ul и Il – Фурье коэффициенты потенциала и тока,соответственно:

	∞				∞
	!				!	(d)		−ilΩ0t
U(t) =	−ilΩ0t	, I	(d)	(t) =					,	(8.49)
	Ul e				l=−∞	Il	e
	l=−∞
Воспользовавшись тем,что
		∞
	U(t − qτ) =	!
		Ul eilΩ0qτ e−ilΩ0t ,

l=−∞

мы получим из( 8.47b) кондактанс :

G(d)	=	e2	T	1 − eilΩ0τ	.	(8.50)
l		h		1 − R eilΩ0τ

Кондактанс G(ld) является нелинейной функцией частоты Ω0, которая изменяет как его величину,так и фазу,определяющую характе р отклика . В частности,при 0 < lΩ0τ mod 2π < π преобладает емкостной отклик,в то время как при π < lΩ0τ mod 2π < 2π преобладает индуктивный отклик. Интересно отметить,что при lΩ0τ mod 2π = π отклик чисто омический и

не зависит от коэффициента прохождения T через КТК, G(ld) = 1/Rq 8.

8Определение Rq было введено после выражения( 8.20) .

243

8.Динамический мезоскопический конденсатор

Cq			R q		Lq

Рис. 8.2.Эквивалентная электрическая цепь,описывающая отклик одномерного кирального кольца,соединенного через квантовый точечный контакт с киральным одномерным проводником

Для того,чтобы изучать отклик мезоскопической системы,ее включают в некоторую электрическую цепь.При этом,чтобы анализир овать протекание тока в такой цепи,необходимо представить изучаемы й мезоскопи - ческий образец в качестве электрического элемента с эквивалентными ему свойствами.В случае рассматриваемой нами модели,такой эл емент должен обладать частотно-зависимой воль-амперной характеристикой.Однако,при небольших частотах, Ω0τ - 1, этот элемент может быть представ - лен как конденсатор с емкостью Cq(d), резистор с сопротивлением Rq(d) и ка -

тушка с индуктивностью L(qd), соединенные последовательно , рис .8.2. Про - водимость такой эквивалентной цепи равна,

1	= Rq + i	6	1	− ωLq	7 .	(8.51)
G(ω)			ωCq

Покажем,что это выражение может быть использовано как пред ел( 8.50) при малых частотах, Ω0 → 0, и выразим параметры эквивалентной элек - трической цепи через характеристики мезоскопического образца,кольца и точечного контакта.

Для этого разложим выражение( 8.50) в ряд по степеням малого пара - метра

lΩ0τ	- 1 ,	(8.52)
T

244

8.2.Емкость кирального одномерного кольца

Выполняя разложение до величин квадратичных по указанному параметру и сравнивая с выражением (8.51) при ω = lΩ0, получим

	e2		h	1			1			h2
Cq(d) =		, Rq(d) =		-		−		.,	Lq(d) =		.	(8.53)
			e2		T		2			12e2

Здесь верхний индекс (d) обозначает величины параметров эквивалентной цепи в случае высокотемпературного режима.

При низких температурах, T0 " T , оба вклада как I(d), так и I(nd) должны учитываться при вычислении тока.Величина I(nd) (8.47c) является нелинейной функцией как амплитуды,так и частоты потенциал а U(t), что существенно затрудняет анализ генерируемого тока.Рассмо трим вначале ток при малой амплитуде возмущающего потенциала.

8.2.6.Линейный отклик

Условие малости осциллирующего потенциала удобно сформулировать для амплитуды каждой его гармоники,

eUl - l!Ω0 ,

(8.54)

что позволяет линеаризовать выражение для I(nd). Сперва рассмотрим ли - неаризованный отклик при нулевой температуре.Тогда удобн о использо - вать( 8.47c),что позволяет получить компактное выражение справедлив ое при произвольной частоте.С другой стороны,если ограничит ься пределом низких частот, Ω0τ - 1, то более удобным оказывается линеаризо - вать непосредственно выражение для амплитуды рассеяния( 8.21),а затем вычислять ток I(t) по формуле( 8.45).В этом случае получается простое выражение,справедливое при произвольной температуре.

8.2.6.1.Проводимость при нулевой температуре

Вычислим фазовые множители в выражении( 8.47c),зависящие от Φs, с точностью до линейных по Ul членов.Затем,учитывая,что при нулевой

245

8.Динамический мезоскопический конденсатор

температуре η(0) = 1, мы может просуммировать по s и q. После этого мы

вычислим G(nd) = I(nd)/Ul, для чего используем следующее преобразование

l

l

∞

(nd)

!

)(nd)

−ilΩ0t

I

(t) = 8

Ul Gl

e

=

l=−∞

Gl(nd)) e−ilΩ0t − Ul Gl(nd)) eilΩ0t

=

∞

I(nd) e−ilΩ0t ,

∞ Ul

!

!

l

l=−∞

2i

l=−∞

I(nd) = Ul G(nd)

, G(nd) =

Gl(nd)) − G−(ndl ))

,

l

l

l

2i

где мы учли,что Ul = U−l поскольку U(t) действительно.

Суммарный кондактанс Gl

= G(d) + G(nd)

равен,

81 + lΩ0τ ln L

l

l

M9

Gl = Gl(d)

1 + R

−2√R cos(χF )

F

. (8.55)

i

2ilΩ0τ

√

ilΩ0

τ

cos(χ )

1 + R e

2

R e

−

Здесь мы используем такие обозначения: r = √

eiχr ,

= kF L + χr −

R

χF

2πeU0/ , где |eU0| - µ0 – среднее по времени значение потенциала.Полученное выражение( 8.55) справедливо при малой амплитуде , но произволь - ной частоте потенциала U(t).

Для того,чтобы определить параметры эквивалентной низкоч астотной электрической цепи,которые при низких температурах мы обо значим через Cq, Rq и Lq, мы разложим выражение (8.55) по степеням малого параметра lΩ0τ → 0 до величин второго порядка малости и после сравнения с выражением( 8.51),получим

246

8.2.Емкость кирального одномерного кольца

e2

T

≡ e2ν(µ0) , Rq =

h

Cq =

√

,

2e2

1 + R − 2 R cos(χF )

(8.56)

√

2

8R

2(1 + R)

2

R cos(χ )

h ν(µ )

4R cos (χ )

Lq =

0

81 +

−

T 2 F

−

F

9,

12e2

где ν(E) = i/(2π)S(E)∂S /∂E – плотность состояний стационарного рассеивателя 9.

Как видим,в случае бесспиновых электронов и одноканальног о кон - такта сопротивление Rq, определяющее диссипативный ток в режиме ли - нейного отклика,является универсальным,в том смысле,что оно не зависит от параметров мезоскопического конденсатора.Такая ун иверсальность была предсказана в работе[ 115] и подтверждена экспериментально в рабо - те[ 117].Она не нарушается даже при учете кулоновского взаимодейс твия. [128, 129, 130, 131, 132] В отличие от этого , в высокотемпературном режи - ме релаксационное сопротивление Rq (8.53) зависит от вероятности про - хождения T через квантовый точечный контакт,соединяющий конденсато р с одномерным киральным проводником ( смотри также работу [133]).

8.2.6.2.Проводимость в пределе низких частот

При низких частотах,

Ω0τ - 1 ,

(8.57)

выразим матрицу рассеяния Флоке( 8.21) через стационарную амплитуду

рассеяния S(U0, E), которая определяется выражением (8.33),вычислен-

√

ным для электрона с волновым числом k(U0) = 2meE/! − 2πeU0/(L ). Для этого разложим U)(t)) = U(t)) − U0, входящее в выражение для Φq(t) в (8.21b),по степеням t) − t,

9Выражение для S(E) приведено в( 8.33).

247

8.Динамический мезоскопический конденсатор

	U)(t))	≈	U)(t) + (t)	−	t)	dU)(t)	+	(t) − t)2	d2U)(t)	,	(8.58)
						dt			dt2
								2

и затем проинтегрируем по t). Раскладывая полученные фазовые множи - тели до членов линейных по U)(t) и удерживая квадратичные по Ω0 члены, получим

Sin(t, E) ≈ S(U0, E) − eU)(t)

∂S(U0, E)

−

i! edU)(t) ∂2S(U0, E)

∂E

2 dt

∂E2

(8.59)

+

!2

ed2U)(t)

∂3S(U0, E)

.

6 dt2

∂E3

Заметим,что первые три члена в этом разложении могут быть оп ределены на основании адиабатического разложения( 8.13),если линеаризовать квазистационарную амплитуду рассеяния по осциллирующей части потенциала

U)(t),

S(t, E) ≡ S (U(t), E) ≈ S (U0, E) + U)(t) ∂S(U0, E) ,

∂U0

пренебречь членами Ω20 и учесть , что в рассматриваемой нами модели

∂S/∂U0 = −e ∂ S/ ∂ E.

Далее мы подставим( 8.59) в выражение (8.45),в котором мы также разложим,

	∂f0			∂2f0 (n!Ω0)2				(8.60)
f0(E) − f0(En) ≈ −		n!Ω0	−				.
	∂E			∂E2		2

После этого окончательно вычислим низкочастотный кондактанс,

248

8.2.Емкость кирального одномерного кольца

∞

(E)

Gl =

ˆ

dE -−

∂f0

.Gl(E) ,

∂E

0

(8.61)

2

2 (lΩ0)2

2

Gl(E) = −ie lΩ0

ν(E) + e h

ν

(E)

2

(lΩ

)3

1 ∂2ν(E)

−ie2h2

0

6

− ν3(E)7.

6

8π2 ∂E2

Очевидно,что при нулевой температуре из вышеприведенного выражения получаются параметры эквивалентной электрической цепи,которые приведены в( 8.56).Можно легко также показать,что при высоких температурах, T0 ( T , выражение (8.61) приводит к параметрам представленным в (8.53).

8.2.7.Нелинейный низкочастотный режим

При низких частотах,смотри( 8.57),возможно получить простое выражение для тока,которое справедливо и в нелинейном режиме,т о есть при нарушении неравенства( 8.54).Для этого подставим( 8.58) в (8.21b) и , удер - живая только члены порядка Ω20, получим

Sin(t, E) = S(t, E) +

i! ∂2S(t, E)

+

!2 ed2U(t) ∂3S(t, E)

2

∂t∂E

6 dt2

∂E3

-

.

(8.62)

−

!2

edU(t)

2

∂4S(t, E)

(Ω0τ)3 .

8

dt

∂E4

+ O

<

=

Напомним,что квазистационарная амплитуда рассеяния опре деляется как S(t, E) = S (U(t), E). Для ее вычисления необходимо сделать замену kL → kL − 2πeU(t)/ в выражении (8.33).Подчеркнем,что выражение( 8.59),

249

8.Динамический мезоскопический конденсатор

будучи нелинейным по постоянной части потенциала U0, является линейным по его осциллирующей части U)(t) = U(t) − U0, в то время как выражение (8.62) является нелинейным по полному зависящему от времени потенциалу

U(t).

Подставляя выражения( 8.62) и (8.60) в выражение (8.45),вычислим низкочастотный нелинейный по напряжению ток: [126]

∞

(E)

<

=

0

I(t) = ˆ

dE -−

∂f0

. J(1)(t, E) + J(2)(t, E) + J(3)(t, E) ,

(8.63a)

∂E

J(1)(t, E) = e2 ν(t, E)

dU(t)

,

(8.63b)

dt

e2h ∂

dU(t)

J(2)(t, E) = −

6ν2(t, E)

7

,

(8.63c)

2

∂t

dt

2h2 ∂2

6-

1 ∂2ν(t, E)

− ν3(t, E).

dU(t)

7

J(3)(t, E) = −

e

6

∂t2

8π2

∂E2

dt

8

9,

(8.63d)

e3h2 ∂

∂

3ν(t, E)

dU(t)

2

−

-

.

96π2

∂t

∂E3

dt

где квазистационарная плотность состояний равна

i

∂S (t, E)

1

∞

rq eiq[kL−2πeU(t)/ ]9.

!q

ν(t, E) = 2π S(t, E)

∂E

=

81 + 2:

=1

(8.64)

Отметим,что в( 8.63) мы использовали ∂ν/∂t = −e(dU/dt) (∂ν/∂E), по - скольку плотность состояний зависит от времени только посредством однородного по периметру кольца осциллирующего потенциала U(t).

250

8.2.Емкость кирального одномерного кольца

Для того,чтобы прояснить физическим смысл выражения( 8.63) по - лезно переписать его следующим образом.Выполняя интегрир ование по энергии один раз по частям,представим его в виде уравнения н епрерывности для заряда кольца Q(t),

I(t) +

∂Q(t)

= 0 ,

(8.65a)

∂t

∞

Q(t) = e ˆ

dEf0(E) νdyn(t, E) ,

(8.65b)

0

νdyn(t, E) = ν(t, E) −

h ∂ν2(t, E)

+

h2 ∂2ν3(t, E)

2

∂t

6

∂t2

(8.65c)

h2 ∂2

2

(t, E)

∂2ν(t, E) dU

2

−

82

∂

ν

−

-

.

9.

96π2 ∂E2

∂t2

∂E2

dt

Величину νdyn(t, E) можно назвать динамической плотностью состо-

яний. Она учитывает эффекты запаздывания , то есть , учитывает то факт , что время,проведенное электроном в кольце не может быть мен ьше чем τ. В результате этого,заряд Q(t), аккумулированный в кольце оказывается за - висящим от частоты Ω0, с которой изменяется потенциал кольца U(t). При малой частоте, Ω0 → 0, эффекты запаздывания учитываются введением в

эквивалентную электрическую цепь сопротивления Rq и индуктивности Lq, соединенных последовательно с емкостью Cq. В режиме линейного отклика эти параметры являются постоянными,смотри( 8.56) для низкотемператур - ного и( 8.53) для высокотемпературного режимов .

В нелинейном же режиме эти параметры оказываются зависящими от потенциала.Поскольку выражение для нелинейной индуктивн ости оказывается довольно громоздким,мы ограничимся рассмотрением эквивалентной электрической цепи,включающей конденсатор и резистор . При этом конденсатор характеризуется нелинейной зависимостью заряда Q от напряжения на нем UC, а резистор имеет нелинейную вольт - амперную харак - теристику.Для описания такой цепи удобно ввести дифференц иальные ха-

251

8.Динамический мезоскопический конденсатор

рактеристики,дифференциальную емкость C∂(UC) = ∂Q(UC)/∂UC и диф - ференциальное сопротивление R∂(V ) = ∂V/∂I(V ). Тогда при Ω0 → 0 ток в такой цепи I(t) зависит от суммарного напряжения U(t) = UC + V следующим образом, [126]

dU

∂

dU

I(t) = C∂

− R∂ C∂

-C∂

..

(8.66)

dt

∂t

dt

Сравнивая выражения( 8.63) и (8.66),получим

∞

dE -−

(E)

.ν(t, E) ,

C∂(t) = e2

ˆ

∂f0

(8.67a)

∂E

´

0

-

.

-

.

∞

dE −

∂f0

∂

ν2(t, E)

dU

h

0

∂E ∂t

dt

R∂(t) =

´

-

∂f0

.

´

-

.

∂

-

.

.

2e2 ∞

dE −

∞

∂f0

dU

0

∂E

ν(t, E) dE −

∂E

∂t

ν(t, E)

dt

0

(8.67b)

Таким образом,в нелинейном режиме при низких частотах кваз истационарная плотность состояний ν(t, E) определяет собственную 10 дифференциальную емкость мезоскопического образца.Это согласует ся с выводами работы[ 115],где рассматривался режим линейного отклика.Отличие заключается в том,что в линейном режиме плотность состояний н е зависит от времени и определяет обычную емкость,тогда как в нелиней ном режиме она определяет дифференциальную емкость.Другое отличи е линейно - го и нелинейного режимов касается эффективного сопротивления.Если в линейном режиме эта величина(при нулевой температуре)уни версальна, Rq = h/(2e2), смотри работу [115] и выражение (8.56),то в нелинейном режиме она оказывается зависящей как от свойств образца(его п лотности состояний),так и от приложенного потенциала U(t).

В заключение отметим , что третий вклад в выражении (8.63), J(3), опре - деляет дифференциальную индуктивность L∂(t) = ∂Φ/∂I , где Φ – магнит-

10В дополнение к геометрической емкости

252

8.2.Емкость кирального одномерного кольца

ный поток,создаваемый катушкой эквивалентной электричес кой цепи.

8.2.8.Релаксационный ток,вызванный скачком потенциала

Вычислим ток в случае,когда потенциала кольца изменился ск ачком

U(t) =		0 ,		t < t0 ,	(8.68)
			,	t > t0 .
	U0

Вообще говоря мы подразумеваем,что потенциал U(t) изменяется от нуля до U0 не мгновенно,а в течение малого интервала времени δt ( !µ−0 1. Это условие необходимо для того,чтобы в выражении для тока( 8.21) мож - но было бы использовать амплитуду рассеяния Sin(t, E) (8.21b),которая была вычислена в предположении,что все существенные для за дачи масштабы энергии много меньше энергии Ферми µ0. С другой стороны интервал времени δt должен быть значительно меньше,чем время,характеризуемо е динамику движения электронов в системе(в нашем случае это в ремя одного оборота τ),для того,чтобы можно было считать изменение потенциала мгновенным.

Подставляя выражение( 8.21) в (8.45) и выполняя интегрирование по энергии получим ток[сравни с выражением( 3.138)]:

I(t) = I(d)(t) + I(nd)(t) ,

e

∞

∂S(q) (t)

!q

I(d)(t) = −i 2π

∂t

,

S(q)(t)

=0

e

∞

η

s T eiskF L

∞

!

!

I(nd)(t) =

+

T s,

8 s=1

Cs(t) , Cs(t) = q=0

πτ

(8.69a)

(8.69b)

S(q+s)(t)S(q) (t) .

(8.69c)

Эти выражения эквивалентны выражениям( 8.47).

253

8.Динамический мезоскопический конденсатор

Подчеркнем,хотя первоначально выражение для тока( 8.45) было по - лучено в рамках формализма матрицы рассеяния Флоке,примен имого в случае периодического изменения потенциала,но это выраже ние может быть переписано в такой форме,которая не использует период ичность во времени,смотри общее выражение( 3.135) и частные выражения (8.47) и (8.69) в качестве примеров . Это позволяет нам вычислить ток , вызванный потенциалом( 8.68) используя выражение (8.69). 11

8.2.8.1.Высокотемпературный ток
Как мы уже говорили,при высоких температурах,								T	0	(	T , только
диагональный вклад в ток сохраняется, I(t) ≈ I					(d)
							(t). Для потенциала U(t)
(8.69) этот ток равен ( дляt ≥ t0): [126]
I(d)(t) =	e2U0		T	RN(t) ,							(8.70)
			τ
где N(t) = [t/τ] – целая часть отношения t/τ.						I(t) = I(d)(t) убывает со
Из полученного выражения следует,что ток

временем как ступенчатая функция,оставаясь постоянным в п ределах интервала времени τ и скачком убывая в R < 1 раз по прошествии каждого интервала времени τ. В масштабе времен , существенно превышающемτ,

можно записать I(t) I0e−(t−t0)/τD , где I0 = e2U0T/h и время τD релаксации тока равно

τ	, .	(8.71)
τD = ln +R1

В случае малого коэффициента прохождения через точечный контакт, T → 0, время релаксации τD ≈ τ/T .

11Формально мы можем считать,что по прошествии времени T/2,намного превосходящем время релаксации тока,потенциал скачком возвращается к исходному значению ,а затем через промежуток времени T/2 опять скачком изменяется до значения U0.Затем все повторяется с периодом T.Поскольку потенциал изменяется периодически во времени,то мы можем без оговорок исполь зовать выражение для тока,полученное в рамках формализма матрицы рассеяния Флоке.Поскольку же пос ледующий скачок потенциала не влияет на ток,вызванный предыдущим скачком,то такой ток не зависит от периода T.Поэтому,можно перейти к пределу T → ∞ и вычислять ток,вызванный непериодическим потенциалом,испол ьзуя выражение для тока, полученное с использованием матрицы рассеяния Флоке.

254

8.2.Емкость кирального одномерного кольца

8.2.8.2.Низкотемпературный ток

При низких температурах, T0 " T , полный ток I(t) = I(d)(t) + I(nd)(t) также экспоненциально убывает со временем.Однако,в допол нение к этому,ток осциллирует с периодом h/(eU0). Для того , чтобы вычислитьI(nd)(t) необходимо сперва вычислить Cs(t) (8.69).Для этого подставим( 8.68) в Eq. (8.21b) и найдем ,

S(q)

Затем вычислим,

		r ,	q = 0 ,
=				e−i		eU0
						!
			e−
		t2rq−1 ×			ieU!0

τq , 1 ≤ q ≤ N ,

t , N + 1 ≤ q .

e−ieU0 τs , 1 ≤ s ≤ N , 1 ≤ N ,

!

S(s)S(0) = −T rs ×

e−ieU!0 t , N + 1 ≤ s , N ,

S(q+s)S(q) = T 2Rq−1rs

e−ieU!0 τ s ,

× ei		eU0	(τq−t) ,
		!
	1 ,

1 ≤ q ≤ N − s , 1 ≤ s ≤ N − 1 , 2 ≤ N ,

N − s + 1 ≤ q ≤ N , s ≤ N , 1 ≤ N ,

1 ≤ q ≤ N , N + 1 ≤ s , 1 ≤ N ,

N + 1 ≤ q , s , N .

(8.72)

(8.73)

(8.74)

255

8.Динамический мезоскопический конденсатор

Окончательно получим,

Cs = γN

(t) T rs RN 1

−

θ(Ni

eU−0

τs)s

χ(t)θ(s

−

N

−

1) ,

R e !

−

eU

)

*

eU

(8.75)

i

0

τ(N+1)

i

0

τ

γN (t) = 1 − T e−i

eU0

t

e

, χ(t) = e−i

eU0

t

1 − e

τ

.

!

!

1 − R e

i

eU0

τ

i

eU0

!

!

1 − R e

Затем используя выражение( 8.69c),получим

∞

∂f

<

=

0

eT

I(nd)(t) =

ˆ

dE -−

0

.

8

J(1)(t, E) + J(2)(t, E) + J(3)(t, E) ,

πτ

∂E

(8.76a)

8

J(1)(t, E) = −RN ln +1 − reikL, 1 − T e−i2π

eU				i2π	eU0	(N+1)			9
		t
				e
0										,	(8.76b)
		τ
				1 − Rei2π			eU0

N≥1 eis(kL−2π

eU0

) rs

81 − T e−i2π

i2π

eU0

(N+1)

9

eU0 t

J(2)(t, E) = −RN

τ

e

,

s

Rs

1

Rei2π

eU0

=1

−

(8.76c)

!s

∞

iskL

s

eU

i2π

eU0

t

!

e

r

−

J(3)(t, E) = (

−

1)

s

e−i2π 0

τ

1 − e

eU0

.

(8.76d)

1 Re−i2π

s=N+1

Заметим,в вышеприведенных выражениях по сравнению с выраж еним (8.69c) мы использовали следующее тождественное преобразование. Ис - пользуя( 8.46) мы возвратили интегрирование по энергии E и затем исполь - зовали следующее тождество,

256

8.2.Емкость кирального одномерного кольца

∞

dEf0(E) e

(E−µ0) = −i

∞

dE -−∂E0

.e

(E−µ0) .

(8.77)

ˆ

i2πs

2πs ˆ

i2πs

∂f

0

0

Выражение( 8.76) значительно упрощается , если скачок потенциала

кратен расстоянию между уровнями энергии, eU0 = n

:

,s

<1 − e−i2π

eU

t

= ,

J(1)(t, E) = −RN lnN1 1− reikL

0

(8.78a)

τ

!

iskL

+

eU0 t

≥

r

J(2)(t, E) = (−1)RN

e

<1 − e−i2π

τ

= ,

(8.78b)

s=1

s

Rs

J(3)(t, E) = 0 .

(8.78c)

Кроме того,если температура равна нулю и уровень Ферми расп оложен точно посередине между уровнями энергии электрона в кольце,тогда rseiskF L = (−1)sRs/2 и полный ток I(t) = I(d)(t) + I(nd)(t) равен,

81 +

+

t

,

ζ(t)9 ,

I(t) =

Q

T RN(t)

sin

2πn

τ

τ

πn

√

(

1)s

(8.79a)

N

!

− s

,

ζ(t) =

−

ln 1 +

R

T

(N

−

1)

)

* −

0

s=1

sR2

t < τ :

81 −

+

,

)

*

(8.79b)

t

9 ,

Q

sin

2πn

τ

ln 1 + √R

I(t) =

T

τ

πn

t ( τ :

81 −

+

t

,

(8.79c)

Q

sin 2πn

τ

√R9 .

I(t) ≈

T RN(t)

ln

τ

πn

257

8.Динамический мезоскопический конденсатор

Сравнивая с( 8.70) мы видим , что как при высоких , так и при низких температурах ток экспоненциально убывает во времени[в сил у множителя RN(t)] с одинаковым временем релаксации τD. Кроме того низкотемпера - турный ток( 8.79) осциллирует во времени [ в силу множителяsin (2πnt/τ)] с периодом равным τ/n = h/(n ).

8.2.8.3.Эмитированный заряд

Вычислим заряд

∞	>	?
0
Q = ˆ	dt Id(t) + I(nd)(t)	,	(8.80)

эмитированный из кольца в результате изменения его потенциала U(t) (8.68).Заметим,что Q может быть как положительным,так и отрицательным в зависимости от знака eU0. Учитывая ступенчатый характер изменения тока во времени,удобно переписать вышеприведенное выраже ние в следующем виде,

	!	(N+1)τ	>	?
		Nτ
Q =	∞	ˆ	dt I(d)(t) + I(nd)(t)	.	(8.81)

N=0

Используя выражения( 8.70) и (8.76),получим

0

-

.

−

2

e

∞

∂f

1

rei(kL−2π

eU0

)

Q =

e U0

+

ˆ

dE

−

0

8ln L

−

M .

(8.82)

π

∂E

1 reikL

При высоких температурах, T0 ( T , эмитированный заряд пропорци - онален величине скачка потенциала, Q = e2U0/ , и изменяется непрерывно при изменении U0. При низких же температурах величина эмитированного

258

8.2.Емкость кирального одномерного кольца

заряда оказывается квантованной в единицах заряда электрона и изменяется скачками при изменении величины U0, рис .8.3. Для того , чтобы пока - зать это,рассмотрим случай,когда коэффициент прохождени я через КТК мал, T → 0. В этом случае зависимость плотности состояний электронов в кольце от энергии может быть апроксимирована суммой дельта-функций

Дирака,расположенных при				E = En, где En уровни энергии электронов в
изолированном кольце.При				µ0 (	спектр электронов в кольце вблизи
µ0 эквидистантный, En	= E0 + n				. Резонансные уровни энергии опреде -
ляются условием θr + k(En)L = 0					mod 2π, где θr – фаза амплитуды от-
ражения для КТК, r =	√
		Reiθr . Преобразуем выражение (8.82).Для этого,
используя kL = 2πE/	и заменяя θr на −k(En)L (при этом мы отбрасы-

ваем величину кратную 2π, которая не влияет на фазу ), может записываем reikL = √Rei2π(E−En)/ = √Rei2π(E−E0)/ . В последнем равенстве мы от -

бросили 2πn в фазе . Дале , подставляяR = 1 и используя следующее тож - дество,

π1 8ln )1 − ei 2π E−E0 * = − 12 + 66E − E0 77 ,

где {{X}} – дробная часть X, мы представим выражение (8.82) в таком виде,

Q =

0

+ e

ˆ

dE

-−∂E0

.-66

−

0 −

0

77

−

66

−

0

77..

e2U

∞

∂f

E

E

eU

E

E

0

(8.83)

Из полученного выражения непосредственно следует,что при нулевой температуре эмитированный заряд квантован в единицах заряда электрона e, смотри рис .8.3. Например , если энергия Фермиµ0 расположена посере-

дине между En и En+1, то есть ,µ = E0 + (n + 0.5)								, тогда
Q = e	::	2	+	eU	0	;;	, kBT0 = 0 ,	T → 0 ,	(8.84)
		1

259

8.Динамический мезоскопический конденсатор

Q / e

3

2

1

0.5

1.5

2.5

3.5 eU0 /

Рис. 8.3.Зависимость величины эмитированного заряда Q (8.83) от величины скачка потенциала U0. Коэффициент прохождения через КТК мал, T → 0. Температура равна нулю . Уровень Ферми расположен посередине между квантовыми уровнями в кольце.

где [[X]] – целая часть X.

При конечных,но все еще низких температурах, kBT0 - , отклонение δQ = Q(T0) − Q от вышеприведенного квантованного значения составляет,

				1 − e(|1−2v0|−1)
δQ = sgn(1	−	2v	)				kBT0	,	(8.85)
		0		|1−2v0|		+ 1
					2kBT0
				e

где v0 = {{eU0/ }} лежит в следующих пределах: 0 ≤ v0 < 1, sgn(X) = +1 для X > 0 и −1 для X < 0. Зависимость δQ(v0) имеет такие асимптотики:

		v0 kBT0 e−							2kBT0	,			v0 → 0 ,
				2											1
				1
δQ(v	) =			,									v0	= 2			0,	(8.86)
0			±													7
				2
				(1 v0) kBT0 e−								2kBT0	, v0		1 .
			−				−		2					→

Таким образом,отклонение от квантованного значения экспо ненциально

260

8.2.Емкость кирального одномерного кольца

мало за исключением того случая,когда величина U0 соответствует переходу от одной ступени зависимости Q(U0) к другой , то есть ,U0 = (n+ 0.5) . Таким образом,резкие края ступеней на рис. 8.3 сглаживаются при увеличении температуры.

Далее мы рассмотрим как влияет увеличение коэффициента прохождения на квантование Q. При конечных , но все же малыхT плотность состояний для рассеивателя,описываемого амплитудой S(E) (8.33),может быть апроксимирована суммой резонансов Брейта-Вигнера[ 134] с шири -

ной % = T /(4π) - ,

ν(E) = 1 ! % . (8.87)

πn (E − En)2 + %2

Вэтом случае при нулевой температуре ,kBT0 = 0, отклонение δQ от Q

(8.84) равно ,

1

arctan

(1−2v0) 2π

δQ =

θ(2v0

1) +

1

T

,

(8.88)

2π

−

−

2

8

−

arctan

9

T

где θ(X) – тета-функция Хевисайда равная нулю для X < 0 м единице для

X > 0. Асимптотики зависимости δQ(v0) такие:

v01πT2 ,

v0 →10 ,

±

7

δQ(v0) =

2 ,

v0 = 2 0 ,

(8.89)

T

−(1 − v0)

π2

, v0 → 1 .

Сравнивая выражения( 8.86) и (8.89),видим,что при конечных значениях коэффициента прохождения величина эмитированного заряда изменяется при отходе от центра ступени, v0 = 0, более сильно , чем при конечных зна - чениях температуры.

261