
- •Лекция 4
- •1.5.Электромагнитные процессы в колебательном контуре с током
- •1. 5.1. Колебательный контур.
- •1.5.2. Уравнение колебательного контура
- •1.5.3. Свободные колебания в контуре
- •1.5.4. Свободные затухающие колебания в контуре
- •1.5.5. Вынужденные электрические колебания.
- •Напряжение на ёмкости отстаёт от силы тока на π/2.
- •1.5.6. Резонанс в последовательном контуре
- •1.5.7. Резонанс в параллельном контуре
- •1.5.8. Переменный ток
1.5.3. Свободные колебания в контуре
Рис.1.5.1.
 Идеальный
колебательный контур, состоящий из
индуктивности L
и ёмкости С, представляет собой линейный
гармонический осциллятор, обладающий
одной степенью свободы.
Идеальный
колебательный контур, состоящий из
индуктивности L
и ёмкости С, представляет собой линейный
гармонический осциллятор, обладающий
одной степенью свободы.
Состояние такого контура в любой момент времени может быть однозначно описано единственным параметром – зарядом q на конденсаторе.
Если сопротивление контура равно нулю, R =0, то при замыкании индуктивности на предварительно заряженный конденсатор с зарядом
 в контуре возникают гармонические
колебания.
в контуре возникают гармонические
колебания.Падение напряжения на конденсаторе
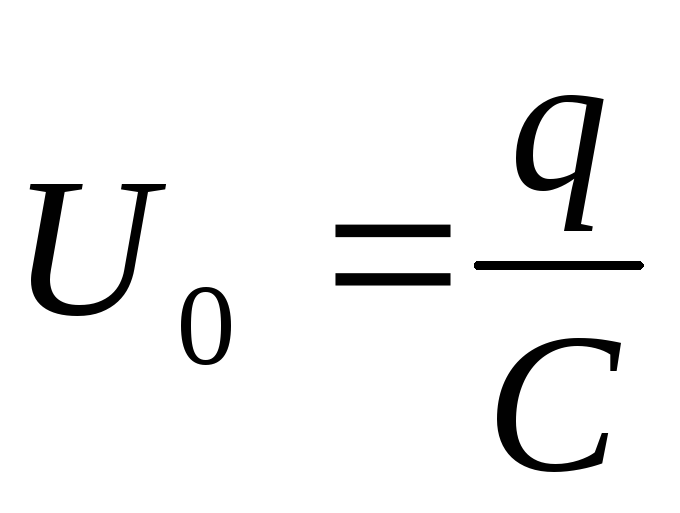 .
.
При замыкании цепи в индуктивности возникает ЭДС индукции
 где ток
где ток  ,
поэтому
,
поэтому 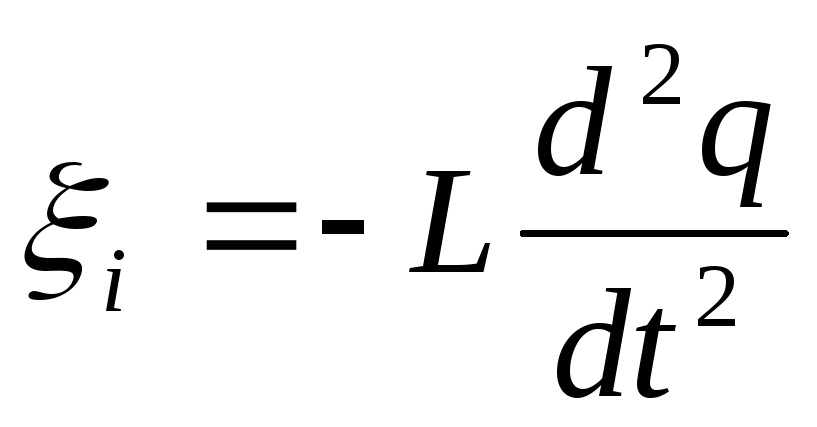 .
.
Согласно второму
правилу Кирхгофа ![]() то есть
то есть
![]() ,
или
,
или ![]()
Это уравнение
является уравнением свободных
гармонических колебаний, при
условии ![]() Его решение
Его решение ![]() ,
,
где ![]() – заряд конденсатора в
момент времени t=0.
– заряд конденсатора в
момент времени t=0.
В катушке:
Для тока имеем:
![]()
- сдвиг фаз между током в контуре
и напряжением на конденсаторе составляет
π/2,
ток опережает по фазе
напряжения на конденсаторе на π/2
(рис.1.5.2).
сдвиг фаз между током в контуре
и напряжением на конденсаторе составляет
π/2,
ток опережает по фазе
напряжения на конденсаторе на π/2
(рис.1.5.2).
Для напряжения закон изменения имеет вид:
![]()
При колебаниях
происходит периодический переход
электрической энергии конденсатора
![]() в магнитную энергию катушки
в магнитную энергию катушки
![]() .
.
При этом полная электромагнитная энергия сохраняется.
1.5.4. Свободные затухающие колебания в контуре
Рис.1.5.3. Всякий реальный
контур
обладает
активным сопротивлением.
Электромагнитная энергия в контуре
постепенно расходуется в этом сопротивлении
на нагревание проводника, вследствие
чего колебания
затухают.
Всякий реальный
контур
обладает
активным сопротивлением.
Электромагнитная энергия в контуре
постепенно расходуется в этом сопротивлении
на нагревание проводника, вследствие
чего колебания
затухают.
По второму правилу Кирхгофа для цепи на имеем:
![]()
Разделим это
уравнение на L
и подставим
![]() ,
,
![]()
Учитывая,
что ![]() ,
и обозначив
,
и обозначив ![]() ,
получаем
,
получаем
![]() - дифференциальное
уравнение затухающих колебаний.
- дифференциальное
уравнение затухающих колебаний.
При ![]() ,
т.е. при
,
т.е. при ![]() ,
,
решение этого
уравнения имеет вид ![]() ,
(1.5.1)
,
(1.5.1)
где ![]() .
.
Подставив ![]() и
и ![]() ,
получаем
,
получаем ![]()
Таким образом,
частота затухающих колебаний
![]() меньше собственной частоты
меньше собственной частоты
![]() .
.
Для определения напряжения на конденсаторе:
разделим
(1.5.1) на С, имеем ![]()
Чтобы найти закон изменения силы тока,
продифференцируем (1.5.1) по времени:
![]()
Обозначим ![]()
тогда ![]()
Так как ![]() то
то ![]()
- при наличии в контуре активного сопротивления
 сила
тока опережает по фазе напряжение на
конденсаторе более чем на
сила
тока опережает по фазе напряжение на
конденсаторе более чем на
![]()
График функции
![]() представлен на рис.1.5.4.
представлен на рис.1.5.4.
Логарифмический декремент затухания
![]()
Он определяется параметрами контура R, L, C и является характеристикой этого контура.
Если затухание невелико
- ![]() ,
то
,
то ![]() и
и ![]()
- добротность
контура в случае слабого затухания
![]()
При слабом затухании добротность контура пропорциональна отношению энергии, запасённой в контуре в данный момент, к убыли этой энергии за один период.
Действительно, амплитуда силы тока в контуре убывает по закону e-βt. Энергия W, запасённая в контуре, пропорциональна квадрату амплитуды силы тока, следовательно W убывает по закону e-2βt.
Относительное уменьшение за период равно:
![]()
При незначительном затухании λ<<1 можно считать e-2λ ≈1-2λ.
Тогда добротность
![]() .
.
При
 частота становится комплексным числом,
и происходит апериодический процесс
разрядки конденсатора.
частота становится комплексным числом,
и происходит апериодический процесс
разрядки конденсатора.
Сопротивление
контура, при котором колебательный
процесс переходит в апериодический,
называется критическим,
![]()
