6. Резонансная частота эквивалентного контура для двух индуктивно связанных контуров.

Резонансная частота для двух индуктивно связанных контуров

Как следует из теории одиночных резонансных контуров, при резонансе в полном сопротивлении резонансного контура мнимая составляющая его равна нулю. Это свойство проявляется во всех системах при резонансе. Этим свойством можно воспользоваться и при определении резонансной частоты двух индуктивно связанных контуров. Для двух индуктивно связанных контуров была найдена эквивалентная схема в виде эквивалентного контура (рис.4.10). Очевидно, что резонансная частота эквивалентного контура является резонансной частотой двух индуктивно связанных контуров.

Исходя из сказанного, резонансная частота эквивалентного контура определяется из условия равенства нулю эквивалентного реактивного сопротивления Х_1Э (4.32). Приравнивая (4.32) к нулю и подставляя выражения для Х₁ и Х₂, получаем исходное уравнение для определения резонансной частоты:

.

Для упрощения анализа рассмотрим случай, когда R₂<<X₂. Это условие практически всегда выполняется. Тогда последнее выражение принимает вид:

.

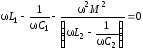Приводя это выражение к общему знаменателю и приравнивая его к нулю, получим:

.

Умножим левую и правую части на ²/L₁L₂:

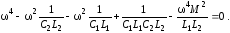
Выполним группировку при ⁴ и ²:

(4.33)

Учитывая (4.17) и используя выражение для резонансной частоты контура, имеем:

(4.34)

С учетом (4.34) уравнение (4.33) примет вид:

(4.35)

Полученное уравнение является биквадратным. В решении при извлечении корня будем брать только положительное значение потому, что отрицательное значение частоты не имеет физического смысла. Так как ₁ и ₂ обозначают резонансные частоты контуров, то для удобства обозначим решение уравнения через .

(4.36)

Рассмотрим значение резонансных частот _1,2 относительно резонансной частоты первого контура. Обозначим эти значения резонансных частот через _1,2:

(4.37)

С учетом (4.37) выражение (4.36) примет вид:

(4.38)

Обозначим отношение резонансной частоты второго контура (₂) к резонансной частоте первого контура (₁) через :

С учетом этого обозначения (4.38) примет вид:

(4.39)

На рис. 4.11 представлены зависимости относительного значения резонансных частот системы двух индуктивно связанных контуров (_1,2) от . Система этих зависимостей (рис.4.11) называется диаграммой Вина. С помощью диаграммы Вина просматриваются некоторые важные свойства индуктивно связанных контуров. Так видно, что при любой настройке контуров, в том числе и одинаковой (=1), система двух связанных контуров имеет две резонансные частоты. Из диаграммы также видно, что при увеличении рассеивания (), а значит, при уменьшении К_СВ (4.17) сближаются значения резонансных частот двух связанных контуров. Наибольшее сближение имеет место при одинаковой настройке контуров (=1).

Рассмотрим найденное соотношение (4.39) при =1, т. е. когда оба контура настроены на одну и ту же частоту (₁=₂=₀).

(4.40)

Помня, что коэффициент связи и коэффициент рассеивания связаны следующими соотношениями (4.17)

выражение (4.40) принимает вид:

(4.41)

Из (4.41) с учетом (4.37) находим резонансные частоты контура ₁ и ₂:

(4.42)

На рис. 4.12 представлена зависимость резонансных частот двух индуктивно связанных контуров от величины коэффициентов связи. Очевидно, что максимальное значение коэффициента связи равно 1.

Только при коэффициенте связи, близком к нулю, резонансные частоты системы связанных контуров, настроенных на одну частоту, практически равны. Увеличение К_СВ ведет к увеличению различия между ними, и при К_СВ=1 это различие равно бесконечности.

Наличие двух резонансных частот приводит к появлению двух экстремальных точек в амплитудно-частотной характеристике системы двух индуктивно связанных контуров (рис. 4.13,а). Характеристика становится "двухгорбой" с провалом между резонансными частотами. Увеличение К_СВ ведет к расширению интервала между резонансными частотами и увеличению провала между ними.

Допущение (R₂<<X₂), что во втором контуре отсутствуют потери, не позволило найти условие, при котором индуктивно связанные два контура имеют одну резонансную частоту при К_СВ0. Вернемся к рассмотрению вопроса о резонансных частотах системы двух связанных контуров без этого допущения. Итак, рассмотрим еще раз условие резонанса Х_1ЭКВ=0:

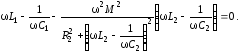
Вынесем за скобки всего уравнения L₁ и из числителя и знаменателя дроби вынесем L₂:

.

Учитывая, что

получаем:

Так как L₁0, то приравняем к нулю выражение в квадратных скобках:

(4.43)

Далее рассмотрим случай, когда оба контура настроены на одну частоту ₁=₂=₀. Текущую частоту обозначим через . С учетом этого выражение (4.43) принимает вид:

(4.44)

Введем обозначение:

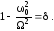(4.45)

Тогда из (4.44) получаем:

(4.46)

Одно решение из (4.46) будет получено при условии =0. Отсюда вытекает, что =₀ (4.45). Это одна из резонансных частот системы контуров.

Другое решение из (4.46) имеет место при приравнивании к нулю круглой скобки, что дает выражение:

.

Решая его относительно , находим:

(4.47)

Решение будет вещественным при следующих условиях:

Первое условие: .

Подставляя (4.45) в (4.47), получим:

Отсюда находим:

(4.48)

Полученные решения (4.48) совпадут с (4.42), если пренебречь потерями во втором контуре (R₂=0), как это делалось раньше.

Второе условие:

Вторым условием существования решения (4.47) является

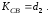(4.49)

Тогда из (4.47) и (4.45) получаем:

Из последнего находим:

(4.50)

При выполнении условия (4.49) система связанных контуров имеет одну резонансную частоту (4.50), а АЧХ имеет "одногорбый" вид (рис. 4.13,б).