6. Последовательный окк – общие соотношения, векторные диаграммы, резонанс, ток и напряжения при резонансе.

Общие понятия

Одиночным колебательным контуром называется электрическая цепь, содержащая элементы C, R, L, соединенные определенным образом, в которой протекает переменный ток. Одиночные контура подразделяются на последовательные и параллельные. Основные свойства контуров характеризуются значительной зависимостью в них электрических процессов от частоты прикладываемого напряжения. В радиотехнических устройствах это напряжение обычно называют входным сигналом. Частота прикладываемого входного сигнала, на которой в контуре токи или напряжения принимают максимальные значения, называется резонансной частотой. Процессы в контуре на резонансной частоте называются резонансными процессами. Обычно контура работают в режимах резонанса. Поэтому часто их называют резонансными контурами.

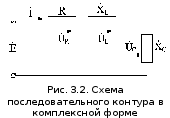
Анализ электрических процессов в одиночном колебательном контуре удобно вести в комплексной форме записи тока, напряжений и сопротивлений элементов контура. Представляя катушку индуктивности и конденсатор в виде комплексного сопротивления, схема последовательного одиночного колебательного контура принимает вид (рис.3.2). Напряжения и ток также представляются в комплексной форме. Входной сигнал и сопротивления реактивных элементов имеют вид:

, , .

Найдем полное сопротивление контура:

, (3.2)

где , , ,

,

.

Здесь и _Z модуль и фаза сопротивления контура, представленного в показательной форме (3.2).

Ток в последовательном одиночном колебательном контуре определяется законом Ома в комплексной форме:

, (3.3)

где – амплитуда тока.

Зная ток контура, находим напряжения на всех элементах контура:

,

где .

,

где .

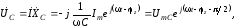
где

При изменении частоты входного сигнала изменяется соотношение между модулями сопротивлений катушки индуктивности и конденсатора. Именно это и определяет все частотные свойства контура. Так, на очень малых частотах:

.

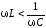На высоких частотах имеет место обратное неравенство:

На какой-то частоте модули сопротивлений этих элементов будут равны: .

Значит, на различных частотах фаза  _z (3.2) будет или отрицательной, или положительной, или равной нулю. Итак, имеют место следующие три случая:

1. , если 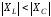- на низких частотах (рис.3.4,а),

2. если - на высоких частотах,

3. , если - на одной частоте.

Для этих трех случаев на рис.3.3 построены векторные диаграммы.

На векторной диаграмме (рис. 3.3, а) при отрицательном значении _z и с учетом минуса в выражении фазы для тока (3.3), фаза тока имеет положительное значение. Вектор тока I находится в первом квадранте. При положительном значении _z (рис. 3.3, б) и с учетом того же минуса в выражении фазы для тока, фаза тока имеет отрицательное значение. Вектор тока находится в четвертом квадранте.

В первом случае ток контура опережает по фазе входное напряжение. Из теории двухполюсников известно, что таким свойством обладает реальный емкостной двухполюсник. Следовательно, контур на низких частотах обладает свойствами емкостного двухполюсника. На высоких частотах (второй случай) ток контура отстает по фазе от входного напряжения и, следовательно, на высоких частотах контур характеризуется свойствами индуктивного двухполюсника.

Резонанс в последовательном одиночном колебательном контуре (резонанс напряжений)

Как отмечалось, при резонансе в контуре электрические процессы экстремальны, т. е. ток и напряжения имеют максимальные значения. Величина тока в контуре при постоянном значении входного ЭДС зависит от величины модуля полного сопротивления контура. При постоянных значениях параметров контура (R, L, C) модуль его полного сопротивления, как следует из (3.2), зависит от частоты.

. (3.4)

На рис.3.4,а показаны зависимости Х_L и Х_C от частоты. На некоторой частоте (=₀) абсолютные величины этих сопротивлений равны (обозначены соответственно Х_L0 и Х_C0).

На рис.3. 4, б показана зависимость модуля полного сопротивления контура от частоты. На частоте =₀ сопротивление контура минимально и равно R. Следовательно, на этой частоте ток в контуре будет максимален и равняется:

. (3.5)

При максимальном токе создается максимальное падение напряжения на элементах. На резисторе оно равно:

. (3.6)

Как увидим в дальнейшем, напряжения на катушке индуктивности и конденсаторе при этой частоте имеют наибольшие значения. Следовательно, режим работы контура на частоте =₀ является резонансным.

При резонансе мнимая составляющая сопротивления контура равна нулю:

. (3.7)

С учетом (3.2) получаем:

; .

Из последнего соотношения находится значение частоты, на которой имеет место резонанс. Эта частота называется резонансной и обозначается ₀:

. (3.8)

С учетом сказанного электрические величины в контуре на резонансной частоте имеют следующие значения:

, . (3.9)

, (3.10)

где .

, (3.11)

где .

, (3.12)

где .

, (3.13)

где.

Так как , то очевидно, что:

. (3.14)

На рис. 3.5 представлена векторная диаграмма тока и напряжений последовательного одиночного контура на резонансной частоте.

Контур, в котором диссипации (потери) стремятся к нулю, называется идеальным. В таком контуре величина R (рис. 3.1) стремится к нулю. Следовательно, на резонансной частоте модуль сопротивления контура (3.9) стремится к нулю, а ток (3.10) стремится к бесконечности.

Подводя итог рассмотренному, отметим, что при резонансе:

1) полное сопротивление контура равно R;

2) фазовый сдвиг между током и входным напряжением равен нулю;

3) напряжение на резисторе R равно ЭДС на входе контура;

4) напряжения на индуктивности и конденсаторе максимальны, равны по величине и противоположны по направлению (фазовый сдвиг между ними равен 180);

5) сопротивление идеального контура стремится к нулю, а ток стремится к бесконечности.

Электрический режим последовательного контура на резонансной частоте называется резонансом напряжений.

6. Последовательный ОКК - амплитудно-частотная и фазо-частотная характеристики, полоса пропускания.

Амплитудно-частотная и фазо-частотная характеристики

Одной из важных электрических величин последовательного контура является его ток. Мы видели, что при изменении частоты изменяется модуль сопротивления контура. Совершенно очевидно, что при изменении частоты ток контура также будет изменяться. Кроме величины тока изменяется и его фаза. Для описания этих свойств контура используются амплитудно-частотные и фазо-частотные характеристики.

Амплитудно-частотной характеристикой называется зависимость модуля комплексного выражения тока контура от частоты входного сигнала. Комплексное выражение тока имеет вид:

. (3.25)

Модуль тока примет вид: . (3.26)

Это выражение, в соответствии с формулировкой, является амплитудно-частотной характеристикой (или сокращенно АЧХ).

На рис.3.7,в соответствии с (3.26), представлена АЧХ одиночного последовательного колебательного контура. На частоте =0, как следует из (3.26), модуль тока равен нулю. При  значение модуля тока стремится также к нулевому значению. При некотором значении частоты выражение (3.26) будет иметь экстремум. Найдем эту частоту, для чего возьмем производную по частоте от (3.26) и приравняем ее к нулю:

.

Из двух сомножителей числителя, зависящих от частоты, только второй может быть равен нулю при определенном значении частоты. Приравнивая его к нулю, находим известное уже выражение для частоты, которую называют резонансной:

; .

Итак, при частоте входного сигнала равной резонансной частоте контура, в контуре ток максимален и равен:

.

Удобно анализировать частотные свойства контура с учетом его добротности и резонансной частоты. Преобразуем полученное выражение АЧХ (3.26). Для этого рассмотрим отдельно выражение под радикалом. Вынесем из него R², а из круглых скобок ₀L.

.

В радиотехнических цепях широко используется понятие обобщенной расстройки, которая обозначается греческой буквой -кси.

. (3.27)

С учетом сделанных преобразований и введенного понятия обобщенной расстройки выражение (3.26) примет вид:

. (3.28)

При анализе влияния величин элементов контура (например, R) на его свойства удобно располагать АЧХ в приведенном (относительном) виде. Приведение выражения (3.28) осуществляется относительно значения АЧХ на резонансной частоте. Для этого разделим левую и правую части (3.28) на модуль тока контура при резонансной частоте (3.10). Обозначим его .

. (3.29)

Тогда на резонансной частоте значение АЧХ (3.29) равно единице. При построении АЧХ в соответствии с (3.29) удобно по оси частот откладывать не абсолютное, а относительное значение частоты  / ₀. Тогда на оси частот резонансной частоте будет соответствовать единица.

На рис.3.8 показано семейство из двух АЧХ для различных значений добротности. Видно, что чем больше добротность контура, тем более узкий вид имеет его АЧХ.

Фазо-частотной характеристикой (ФЧХ) называется зависимость от частоты величины угла фазового сдвига тока относительно приложенного напряжения и обозначается ().

,

где _U - фаза приложенного к контуру напряжения, _I() - фаза тока.

Обычно, в теоретическом анализе, фаза приложенного к контуру напряжения задается равной нулю (_U=0). Тогда фазо-частотная характеристика представляет собой значение фазы тока контура, взятого с противоположным знаком:

. (3.30)

Ток контура (3.25), выраженный через добротность и резонансную частоту, имеет вид:

.

Из этого выражения тока находим фазовую характеристику тока:

.

Фазо-частотная характеристика контура, с учётом (3.30), отличается только знаком.

.

На рис.3.9 представлены графики этих фазовых характеристик.

Фазо-частотная характеристика, как следует из формулировки, показывает изменение разницы между фазой приложенного напряжения и фазой тока. Фазовая характеристика тока _I() показывает фазовое положение вектора тока на векторной диаграмме относительно вектора приложенного напряжения. Она дает информацию о свойствах контура на различных частотах. Так на резонансной частоте фазовый сдвиг между током и напряжением на входе равен нулю. Это имеет место только в резистивном двухполюснике. Следовательно, на резонансной частоте последовательный контур обладает свойствами резистивного двухполюсника.

На частоте меньше резонансной, как видно из графика, фаза тока по отношению к входному сигналу положительная, т. е. в области частот от нуля до резонансной ток в контуре опережает входное напряжение. Это имеет место только в емкостном реальном двухполюснике. Следовательно, в этой области частот последовательный контур может быть заменен последовательно соединенным резистором R и эквивалентным конденсатором C_ЭКВ. Отметим, что величина C_ЭКВ отличается от величины собственного конденсатора контура и определяется выражением:

.

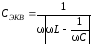На частотах больше резонансной фаза тока отрицательна по отношению к входному напряжению, т. е. в области частот от резонансной частоты в сторону ее увеличения ток отстает по фазе от входного напряжения. Как рассматривалось ранее, это имеет место только в индуктивном реальном двухполюснике. Следовательно, в этой области частот последовательный контур может быть заменен последовательно соединенными резистором R и эквивалентной индуктивностью L_ЭКВ. Величина эквивалентной индуктивности отличается от величины собственной индуктивности контура и определяется выражением:

.