3.3.2. Параллельный колебательный контур с диссипацией в реактивных ветвях

Схема параллельного контура с диссипацией в реактивных ветвях представлена на рис.3.24,а.

Общие соотношения для контура.

Сопротивление контура. Сопротивление каждой из ветвей контура равно:

; , (3.69)

где ,

, .

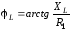
Сопротивление всего контура (рис.3.24,б) равно:

.

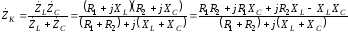В резонансных контурах выполняется условие:

R_1<<X_L; R_2<<X_C.

Тогда произведениями R₁R₂, R₁X_С и R₂X_L в числителе можно пренебречь. В знаменателе суммой (R₁ + R₂) пренебречь нельзя, т. к. при определенной частоте (Х_L + Х_C) равно нулю и на этой частоте будет выполняться условие:

(R₁+R₂)>>(X_L+X_C).

С учетом сказанного выражение для сопротивления контура принимает вид:

.

Обозначим R = R₁ + R₂.

Запишем окончательное выражение для сопротивления контура:

. (3.70)

Представим сопротивление контура (3.70) в показательной форме:

,

где

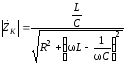, . (3.71)

Напряжения и токи в контуре. Как отмечалось, контурный ток i_К(t) имеет нулевую фазу и в комплексной форме имеет вид:

. (3.72)

Напряжение на контуре определяется очевидным выражением:

, (3.73)

где

Контурное напряжение приложено ко всем ветвям. С учетом (3.69) определяем токи в ветвях контура:

, где .

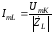(3.74)

, где .

Токи в ветвях создают падения напряжений на элементах этих ветвей. Найдём напряжения на элементах ветвей (3.75):

,

где ;

,

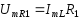где

; (3.75)

,

где ;

,

где .

Резонанс в контуре. Для рассмотрения резонансных свойств контура представим его сопротивление (3.70) в алгебраической форме. Умножим числитель и знаменатель (3.70) на комплексно-сопряженное знаменателю выражение и выделим вещественную и мнимую части:

. (3.76)

Резонансная частота контура может быть определена из условия равенства нулю мнимой части комплексного сопротивления контура. Из (3.76) видно, что условием резонанса является следующее равенство:

.

Тогда резонансная частота контура определяется известным уже соотношением:

. (3.77)

Сопротивление контура при резонансе, которое обозначим как , находится из (3.70) с учётом условия резонанса и имеет вид:

.

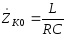В соответствии с (3.71) получаем:

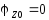, . (3.78)

Напряжения и токи в контуре при резонансе определяются из (3.73), (3.74) и (3.75) с учётом значения модуля и фазы сопротивления контура на резонансной частоте (3.78). Тогда напряжение на контуре, токи в ветвях и напряжения на элементах ветвей определяются с помощью следующих соотношений (3.79):

,

где ;

, где ;

, где; (3.79)

, где ;

, где ;

, где ;

, гдe .

Для высокодобротных контуров R₁ и R₂ пренебрежимо малы по сравнению с Х_L и Х_C. Тогда можно считать, что

, .

По результатам (3.79) на рис.3.25 построена векторная диаграмма токов и напряжений одиночного параллельного контура с диссипациями в реактивных ветвях на резонансной частоте.

Пример.

Дано: U_{m Вх} = 10 В ; R₁ = R₂ = 1 Ом ;

L = 1,6 мГн ; С = 25 мкФ.

Найти: контурный ток и токи в ветвях, напряжения на элементах, построить векторную диаграмму.

Ответы: I_{m K} = 0,312 A, I_mC= I_mL=1,24 A,

, U_{m R1} = U_{m R2} =1,24 В ,

U _mC= U_mL = 9,92 В.

Мощности в контуре. Мгновенную и среднюю мощности контура найдем как сумму мгновенных и средних мощностей каждой ветви контура. Для этого вначале определим мгновенные и средние мощности каждой ветви.

С учетом (3.79) находим мгновенную мощность в индуктивной ветви:

Определяем cos_L и sin_L из треугольника сопротивления (рис.2.16) с учетом используемых здесь обозначений и (3.79)

, , .

С учетом полученных соотношений мгновенная мощность в индуктивной ветви принимает вид:

.

Амплитуда реактивной мощности этой ветви равна:

.

Находим среднюю мощность индуктивной ветви контура:

.

Определяем мгновенную мощность в емкостной ветви контура:

Определяем sin_C и cos_C из треугольника сопротивлений (рис.2.10,а) с учетом используемых здесь обозначений и (3.78):

, , .

С учетом полученных соотношений мгновенная мощность на емкостной ветви принимает вид:

.

Амплитуда реактивной мощности этой ветви равна:

.

Находим среднюю мощность емкостной ветви контура:

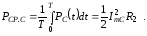
Так как токи I_mL и I_mC равны, то в дальнейшем каждый из них будем обозначать через I_m:

.

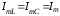Мгновенную и среднюю мощности контура находим суммированием мгновенных и средних мощностей ветвей контура:

.

Добротность контура. В выражении мгновенной мощности контура отсутствует реактивная мощность. Это вызвано тем, что реактивные мощности каждой ветви при резонансе имеют одинаковые амплитуды и противоположны по фазе. Поэтому при определении добротности контура используются амплитуды реактивной мощности или индуктивной ветви или емкостной:

, (3.80)

где и - амплитуды реактивных мощностей индуктивной и емкостной ветвей контура.

Учитывая, что

,

добротность можно выразить через характеристическое сопротивление : .

Следует обратить внимание на то, что выражение (3.80) отличается от выражения определения добротности параллельного контура без диссипации в реактивных ветвях (3.57). Действительно, в рассматриваемом контуре (с диссипациями в реактивных ветвях) чем меньше R₁ и R₂, тем меньше теряется на них мощность, тем меньше затухают колебания в контуре.

Сопротивление контура с учетом резонансной частоты и добротности. Одна из форм комплексного сопротивления контура имеет вид (3.71):

.

Используя выражения для резонансной частоты (3.74) и добротности (3.80), получим:

Находим модуль и фазу комплексного сопротивления контура:

, (3.81)

На резонансной частоте модуль сопротивления контура равен:

(3.82)

На рис.3.26 представлена зависимость модуля комплексного сопротивления контура (3.81) от частоты. Она имеет куполообразный характер с максимальным значением на резонансной частоте.

Из (3.82) видно, что c увеличением добротности контура возрастает его сопротивление.

Амплитудно-частотная характеристика рассматриваемого контура есть зависимость от частоты модуля отношения напряжения на контуре при произвольной частоте к напряжению на контуре при резонансной частоте. Вначале представим отношение этих напряжений в комплексной форме и, с учетом (3.81) и (3.82), находим:

. (3.83)

Из (3.83) выражение для амплитудно-частотной характеристики, в соответствии с данной формулировкой, принимает вид:

.

Полученное выражение полностью совпадает с выражением для АЧХ параллельного контура без диссипаций в реактивных ветвях (3.65). Соответственно совпадают и их графики (рис.3.20).

Фазо-частотная характеристика контура есть зависимость фазы напряжения на контуре от частоты. Из (3.73) и (3.81) находим:

.

Данное выражение фазо-частотной характеристики полностью совпадает с выражением ФЧХ для параллельного контура без диссипаций в реактивных ветвях (3.66). Очевидно, что и график ФЧХ (рис.3.21) и результаты его анализа полностью соответствуют рассматриваемому здесь контуру (рис.3.24).

Полоса пропускания. В связи с идентичностью амплитудно-частотных характеристик контура с диссипациями в реактивных ветвях (3.83) и контура без диссипаций в реактивных ветвях (3.65), формулы определения полосы пропускания этих контуров также идентичны и имеют вид (3.68):

.

Отличительная особенность во всех названных случаях состоит в различии определения добротности в контуре с диссипациями в реактивных ветвях (3.80) и в контуре без диссипаций в реактивных ветвях (3.61).

Влияние R₁ и R₂ на резонансную частоту контура. В низкодобротных контурах величины R₁ и R₂ заметны и их необходимо учитывать при определении резонансной частоты контура. Для параллельного контура с диссипацией в реактивных ветвях (рис.3.24) найдем полную проводимость контура:

Как отмечалось, при резонансе полное сопротивление контура становится вещественным. Следовательно, вещественной величиной будет и проводимость контура. Значит, на резонансной частоте мнимая часть проводимости равна нулю.

; .

После некоторых преобразований находим:

, (3.84)

где – волновое сопротивление.

Видно, что если величинами R₁ и R₂ можно пренебречь, то формула (3.84) преобразуется в (3.77). Изменяя величины R₁ и R₂ можно изменять резонансную частоту в некоторых пределах.