3.9. Распределение Больцмана при дискретных уровнях

Полученное Больцманом распределение относится к случаям, когда молекулы находятся во внешнем поле и их по­тенциальная энергия U может изменяться непрерывно. С ростом U концентрация частиц уменьшается.

Больцман обобщил свой закон на случай распределения, зависящего от внутренней энергии E молекулы (атома). Изве­стно, что величина E в этом случае может принимать лишь ди­скретный ряд дозволенных значений, и соответствующее рас­пределение Больцмана записывают так:

.

где 1 и 2— два произвольных (интересующих нас) уровня (состояния), — отношение числа частиц на этих уровнях, которым отвечают внутренние энергиии,g — кратность вырожде­ния каждого уровня. Например, кратность вырождения энерге­тического уровня атома водорода с главным квантовым числом n равна g = 2n²; кратность вырождения колебательного уровня двухатомной молекулы g = 1, а у вращательных уровней g = 2r+1, где r — вращательное квантовое число.

Именно в таком виде распределение Больцмана для дискрет­ного спектра используется наиболее часто.

Рассмотрим пример. Макросистема состоит из N частиц, которые могут находить­ся в двух состояниях, 1 и 2, с внутренними энергиями и, причем. Известно, что. Найдем зависимость среднего числа частиц в состоя­нии 2 от температуры T системы.

Вданном случае

,

где. Исключив из этих двух уравнений, полу­чим

.

На рис. 3.12 приведен график зависимости .

3.10. Закон распределения Максвелла—Больцмана

Распределения Максвелла и Больцмана являются составны­ми частями единого распределения, называемого распределени­ем Гиббса .

Оба разобранных нами распределения можно объединить в один закон распределения Максвелла-Больцмана, согласно ко­торому число dN молекул, проекции скорости которых и их ко­ординаты лежат в интервалах ,определяется выражением

где нормировочный множитель U = U(x, y, z).

3.10.Каноническое распределение гиббса

Большинство встречающихся на практике систем не являются изолированными. Они могут обмениваться теплом со своим окружением. Если такая система мала по сравнению с окружающей средой, она может рассматриваться как система, находящаяся в контакте с тепловым резервуаром, коим является все окружение системы. Мы будем иметь дело с относительно малой системой А в контакте с тепловым резервуаром . СистемойА может быть любая относительно малая макроскопическая система. Нас интересует вероятность того, что в состоянии равновесия мы обнаружим системуА в состоянии с энергией.

Разделим шкалу энергий на небольшие интервалы и обозначим черезчисло доступных состояний системы, когда ее энергия равна, т.е. лежит в интервале. Закон сохранения энергии требует, чтобы энергия системыА и резервуара оставалась постоянной величиной:.

Но если система А находится в одном определенном состоянии , число доступных состояний всей системы( системаА и резервуар ) просто равно числу состояний, доступных. Изолированную системуможно обнаружить с равной вероятностью в любом из ее доступных состояний. Поэтому вероятность ситуации «системаА находится в состоянии » пропорциональна числу доступных состояний системы, когдаА находится в состоянии :

.

Система Агораздо меньше резервуара, поэтому. Разложим медленно меняющийся логарифмоколо значения=:

где -значение производной при фиксированной энергии =. Эта величина является постоянным температурным параметром теплового резервуара ,. Тогда получаем

Величина является постоянной, не зависящей от r, поэтому вероятность

=(3.9) Здесь С – константа, не зависящая отr.

Если система А находится в состоянии с большой энергией, то на долю резервуара приходится соответственно меньшая энергия, поэтому число доступных состояний резервуара существенным образом уменьшается. В соответствии с этим уменьшением вероятность осуществления такой ситуации также уменьшается.

Выражение (3.9) является весьма общим результатом, имеющим огромное значение в статистической физике. Экспоненциальный множитель называется множителем Больцмана, а распределение вероятностей(3.9) – каноническим распределением. Ансамбль систем, находящихся в контакте с тепловым резервуаром известной температуры, называется каноническим ансамблем.

Постоянная С в выражении (3.9) может быть найдена из условия нормировки:

.

Эта сумма распространяется на все возможные состояния системы А, независимо от энергии. Из условия нормировки с учетом (3.9) получаем , и

Классическое приближение совершенно непригодно при достаточно низких температурах. Действительно, допустим, что характеристическая тепловая энергия ( - среднее расстояние между уровнями энергии системы). В этом случае квантование возможных значений энергии системы весьма существенно определяет ее поведение. Например, из канонического распределения(3.9) следует, что вероятность нахождения системы в двух состояниях с энергией Е и , где - квант энергии, в случае весьма различна. С другой стороны, если , то вероятности очень мало меняются при переходе от данного к ближайшему состоянию. В этом случае дискретность перестает быть быть существенной и классическое приближение становится оправданным.

Рассмотрим замкнутую макросистему с энергией и числом частицn=const. Определим вероятность Р(;n) застать систему в состоянии Е_i при фиксированном числе частиц n. Каждому значению иn отвечает некоторая группа состояний Г(;n). Т.к. все состояния с данной энергией и числом частиц равноправны или равновероятны, то вероятность того, что замкнутая система находится в одном из них, будет пропорциональна числу состояний с данной энергией и данным числом частиц :

Р(;n)  Г(;n)

- это микроканоническое распределение Гиббса. Оно показывает, что вероятность нахождения замкнутой системы в одном из состояний с данной энергией пропорциональна кратности выражения (т.е. числу состояний с данной энергией). Чем больше состояний системы с данной энергией, тем с большей вероятностью можно застать систему в одном из них. Распределение Гиббса является принципиальной основой статистической физики.

На практике часто приходится иметь дело с незамкнутыми системами. Потому, систему представляют находящуюся в термостате. Возможен обмен энергией и частицами между системой и термостатом. В термостат можно включить все тела, с которыми взаимодействует система, и систему ‘’система А - термостат’’ можно считать замкнутой +Е_B =Е; n + N_B = N, где Е_B - энергия термостата, N_B - число частиц термостата.

Пусть Р(;n) и Р(Е_B ;N_B) - вероятность состояния системы А и термостата В.

Вероятность того, что система А находится в состоянии (;n); а термостат В - в состоянии (Е_B ;N_B) равна произведению вероятностей

Р = Р(;n)Р(Е_B ;N_B) Г(Е;N).

Размеры термостата много больше размеров системы А, поэтому Е_B>>;N_B>>n, и каким бы не было изменение системы А, состояние термостата остается практически неизменным, т.е. Р(Е_B ;N_B)= const , и

Р(;n) Г(Е;n)=Г(Е-;N-n) Г(;n).

Из этого выражения можно получить большое каноническое распределение Гиббса, которое определяет вероятность застать систему А с энергией и числом частицn в одном из состояний Г(;n):

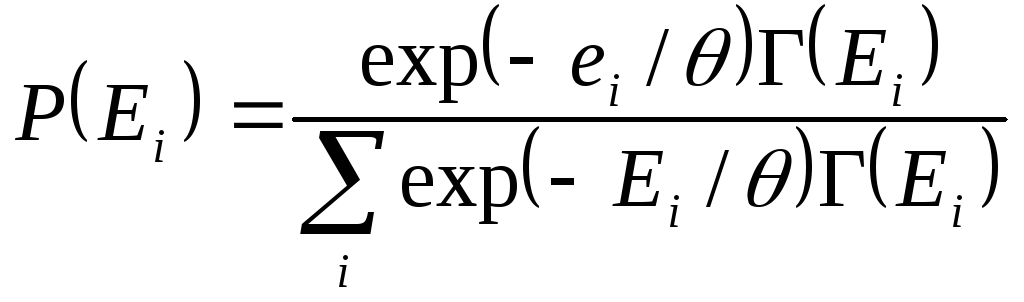. (3.10)

Здесь  - модуль канонического распределения . Он характеризует свойства всего окружения или термостата В, но не выделенной нами системы А. Модуль распределения  является функцией энергии макроскопической системы, причем эта зависимость однозначная.  - величина существенно положительная.

 является характеристикой состояния равновесия макроскопической системы. Это означает, что если у двух равновесных макросистем совпадают модули канонического распределения, то в случае контакта между системами, совокупная система будет находиться в состоянии равновесия. Если же  у системы различны, то при контакте равновесия не будет.

Величину  еще называют статистической температурой. Она имеет размерность энергии и равна  = kТ , где k - постоянная Больцмана.

В классической физике энергия системы меняется непрерывно, поэтому вместо дискретно изменяющегося индекса i в выражение (3.10) следует подставить непрерывно изменяющуюся совокупность координат и импульсов частиц E=E(x;p), и статистическая сумма должна быть заменена на статистический (или фазовый) интеграл

,

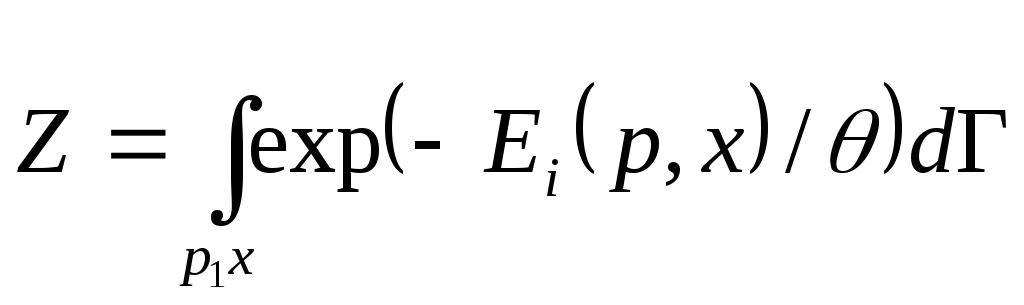где dГ число состояний системы с энергией E;E+ dE.

Само каноническое распределение Гиббса в классическом приближении примет вид:

,

где - вероятность застать частицы системы в состоянии с координатамиx ; x + dx и импульсами p ; p + dp , или вероятность данного микросостояния.

Интегрирование ведется по всему фазовому пространству, т.е. по всем дозволенным значениям импульсов и координат, dГ=dxdp , тогда .