Varian Microeconomics Workout

price if he wants it. What is the highest posted price at which he would

be willing to buy the painting?

.

(b) On another day, Steve and Leroy see each other at the auction, sni±ng all of the paintings. No other customers have appeared at the auction house. In deciding how much to bid for a painting that passes his sni® test, Steve considers the following: If a painting is selected at random and sni®ed by both Steve and Leroy, there are ¯ve possible outcomes. Fill in the blanks for the probability of each.

² Genuine and passes both dealers' tests. Probability:					.
² Fake and passes both dealers' tests. Probability:					.
² Fake and passes Steve's test but fails Leroy's. Probability:					.
² Fake and passes Leroy's test but fails Steve's. Probability:					.
² Fake and fails both dealers' tests. Probability:					.

(c) On the day when Steve and Leroy are the only customers, the auction house sets a reserve price of $300. Suppose that Steve believes that Leroy will o®er to buy any painting that passes his sni® test. Recall that if Steve and Leroy both bid on a painting, the probability that Steve gets it is only 1/2. If Steve decides to bid on every painting that passes his own sni® test, what is the probability that a randomly selected painting is genuine

and that Steve is able to buy it? What is the probability that a randomly selected painting is a fake and that Steve will bid on it and get

it? If Steve o®ers to pay $300 for every painting that passes his

sni® test, will his expected pro¯t be positive or negative?

Suppose that Steve knows that Leroy is willing to pay the reserve price for any painting that passes Leroy's sni® test. What is the highest reserve price that Steve should be willing to pay for a painting that passes his

own sni® test?

.

17.10 (2) Every day the Repo ¯nance company holds a sealed-bid, second-price auction in which it sells a repossessed automobile. There are only three bidders who bid on these cars, Arnie, Barney, and Carny. Each of these bidders is a used-car dealer whose willingness to pay for another used car °uctuates randomly from day to day in response to the variation in demand at his car lot. The value of one of these used cars to any dealer, on any given day is a random variable which takes a high value $H with probability 1=2 and a low value $L with probability 1=2. The value that each dealer places on a car on a given day is independent of the values placed by the other dealers.

Each day the used-car dealers submit written bids for the used car being auctioned. The Repo ¯nance company will sell the car to the dealer with the highest bid at the price bid by the second-highest bidder. If there is a tie for the highest bid, then the second-highest bid is equal to the highest bid and so that day's car will be sold to a randomly selected top bidder at the price bid by all top bidders.

(a) How much should a dealer bid for a used car on a day when he places

a value of $H on a used car?

How much should a dealer bid

for a used car on a day when he places a value of $L on a used car?

.

(b) If the dealers do not collude, how much will Repo get for a used car

on days when two or three dealers value the car at $H? How much will Repo get for a used car on days when fewer than two dealers

value the car at $H? .

(c) On any given day, what is the probability that Repo receives $H

for that day's used car?				What is the probability that Repo
receives $L for that day's used car?					What is Repo's expected
revenue from the sale?						.

(d) If there is no collusion and every dealer bids his actual valuation for every used car, what is the probability on any given day that Arnie gets a car for a lower price than the value he places on it? (Hint: This will happen only if the car is worth $H to Arnie and $L to the other

dealers.) Suppose that we measure a car dealer's pro¯t by the di®erence between what a car is worth to him and what he pays for it. On

a randomly selected day, what is Arnie's expected pro¯t? .

(e) The expected total pro¯t of all participants in the market is the sum of the expected pro¯ts of the three car dealers and the expected revenue realized by Repo. Used cars are sold by a sealed-bid, second-price auction and the dealers do not collude. What is the sum of the expected pro¯ts

of all participants in the market?

.

17.11 (3) This problem (and the two that follow) concerns collusion among bidders in sealed-bid auctions. Many writers have found evidence

that collusive bidding occurs. The common name for a group that practices collusive bidding is a \bidding ring."*

Arnie, Barney, and Carny of the previous problem happened to meet at a church social and got to talking about the high prices they were paying for used cars and the low pro¯ts they were making. Carny complained, \About half the time the used cars go for $H, and when that happens, none of us makes any money." Arnie got a thoughtful look and then whispered, \Why don't we agree to always bid $L in Repo's used-car auctions?" Barney said, \I'm not so sure that's a good idea. If we all bid $L, then we will save some money, but the trouble is, when we all bid the same, we are just as likely to get the car if we have a low value as we are to get it if we have a high value. When we bid what we think its worth, then it always goes to one of the people who value it most."

(a) If Arnie, Barney, and Carny agree to always bid $L, then on any given day, what is the probability that Barney gets the car for $L when it is

actually worth $H to him?			What is Barney's expected pro¯t
per day?				.

(b) Do the three dealers make higher expected pro¯ts with this collusive

agreement than they would if they did not collude? Explain.

.

(c) Calculate the expected total pro¯ts of all participants in the market (including Repo as well as the three dealers) in the case where the dealers

collude.		Are these expected total pro¯ts

larger or smaller than they are when the dealers do not collude?

.

(d) The cars are said to be allocated e±ciently if a car never winds up in the hands of a dealer who values it less than some other dealer values it. With a sealed-bid, second-price auction, if there is no collusion, are

the cars allocated e±ciently?		If the dealers collude as in this
problem, are the cars allocated e±ciently?				.

17.12 (2) Arnie, Barney, and Carny happily practiced the strategy of \always bid low" for several weeks, until one day Arnie had another idea.

* Our discussion draws extensively on the paper, \Collusive Bidder Behavior at Single-Object, Second-Price, and English Auctions" by Daniel Graham and Robert Marshall in the Journal of Political Economy, 1987.

Arnie proposed to the others: \When we all bid $L, it sometimes happens that the one who gets the week's car values it at only $L although it is worth $H to somebody else. I've thought of a scheme that will increase pro¯ts for all of us." Here is Arnie's scheme. Every day, before Repo holds its auction, Arnie, Barney and Carny will hold a sealed-bid, second-price preauction auction among themselves in which they bid for the right to be the only high bidder in that day's auction. The dealer who wins this preauction bidding can bid anything he likes, while the other two bidders must bid $L. A preauction auction like this is known is a \knockout." The revenue that is collected from the \knockout" auction is divided equally among Arnie, Barney, and Carny. For this problem, assume that in the knockout auction, each bidder bids his actual value of winning the knockout auction.*

(a) If the winner of the knockout auction values the day's used car at $H, then he knows that he can bid $H for this car in Repo's second-price sealed-bid auction and he will get it for a price of $L. Therefore the value of winning the knockout auction to someone who values a used car at

$H must be		The value of winning the knockout auction to
someone who values a used car at $L is				.

(b) On a day when one dealer values the used car at $H and the other

two value it at $L, the dealer with value $H will bid						in
the knockout auction and the other two dealers will bid					In this
case, in the knockout auction, the dealer pays				for the right to

be the only high bidder in Repo's auction. In this case, the day's used

car will go to the only dealer with value $H and he pays Repo

for it. On this day, the dealer with the high buyer value makes a total

pro¯t of .

(c) We continue to assume that in the knockout auction, dealers bid their actual values of winning the knockout. On days when two or more buyers

value the used car at $H, the winner of the knockout auction pays

for the right to be the only high bidder in Repo's auction.

* It is not necessarily the case that this is the best strategy in the knockout auction, since one's bids a®ect the revenue redistributed from the auction as well as who gets the right to bid. Graham and Marshall present a variation on this mechanism that ensures \honest" bidding in the knockout auction.

(d) If Arnie's scheme is adopted, what is the expected total pro¯t of each of the three car dealers? (Remember to include each dealer's share of the

revenue from the knockout auction.)

.

17.13 (2) After the passage of several weeks during which Repo never got more than one high bid for a car, the Repo folks guessed that something was amiss. Some members of the board of directors proposed hiring a hit man to punish Arnie, Barney, and Carny, but cooler heads prevailed and they decided instead to hire an economist who had studied Intermediate Microeconomics. The economist suggested: \Why don't you set a reserve price $R which is just a little bit lower than $H (but of course much larger than $L)? If you get at least one bid of $R, sell it for $R to one of these bidders, and if you don't get a bid as large as $R, then just dump that day's car into the river. (Sadly, the environmental protection authorities in Repo's hometown are less than vigilant.) \But what a waste," said a Repo o±cial. \Just do the math," replied the economist.

(a) The economist continued. \If Repo sticks to its guns and refuses to sell at any price below $R, then even if Arnie, Barney, and Carny collude, the best they can do is for each to bid $R when they value a car at $H and to bid nothing when they value it at $L." If they follow this strategy,

the probability that Repo can sell a given car for $R is			, so Repo's
expected pro¯t will be				.

(b) Setting a reserve price that is just slightly below $H and destroying cars for which it gets no bid will be more pro¯table for Repo than setting

no reservation price if the ratio H=L is greater than			and less
pro¯table if H=L is less than				.

In this chapter you work with production functions, relating output of a ¯rm to the inputs it uses. This theory will look familiar to you, because it closely parallels the theory of utility functions. In utility theory, an indi®erence curve is a locus of commodity bundles, all of which give a consumer the same utility. In production theory, an isoquant is a locus of input combinations, all of which give the same output. In consumer theory, you found that the slope of an indi®erence curve at the bundle (x1; x2) is the ratio of marginal utilities, MU1(x1; x2)=MU2(x1; x2). In production theory, the slope of an isoquant at the input combination (x1; x2) is the ratio of the marginal products, MP1(x1; x2)=MP2(x1; x2). Most of the functions that we gave as examples of utility functions can also be used as examples of production functions.

There is one important di®erence between production functions and utility functions. Remember that utility functions were only \unique up to monotonic transformations." In contrast, two di®erent production functions that are monotonic transformations of each other describe di®erent technologies.

If the utility function U(x1; x2) = x1 + x2 represents a person's preferences, then so would the utility function U¤(x1; x2) = (x1+x2)2. A person who had the utility function U¤(x1; x2) would have the same indi®erence curves as a person with the utility function U(x1; x2) and would make the same choices from every budget. But suppose that one ¯rm has the production function f(x1; x2) = x1 + x2, and another has the production function f¤(x1; x2) = (x1 + x2)2. It is true that the two ¯rms will have the same isoquants, but they certainly do not have the same technology. If both ¯rms have the input combination (x1; x2) = (1; 1), then the ¯rst ¯rm will have an output of 2 and the second ¯rm will have an output of 4.

Now we investigate \returns to scale." Here we are concerned with the change in output if the amount of every input is multiplied by a number t > 1. If multiplying inputs by t multiplies output by more than t, then there are increasing returns to scale. If output is multiplied by exactly t, there are constant returns to scale. If output is multiplied by less than t, then there are decreasing returns to scale.

Consider the production function f(x1; x2) = x11=2x32=4. If we multiply the amount of each input by t, then output will be f(tx1; tx2) =

(tx1)1=2(tx2)3=4. To compare f(tx1; tx2) to f(x1; x2), factor out the expressions involving t from the last equation. You get f(tx1; tx2) =

t5=4x11=2x32=4 = t5=4f(x1; x2). Therefore when you multiply the amounts of all inputs by t, you multiply the amount of output by t5=4. This means

there are increasing returns to scale.

Let the production function be f(x1; x2) = minfx1; x2g. Then

f(tx1; tx2) = minftx1; tx2g = min tfx1; x2g = t minfx1; x2g = tf(x1; x2):

Therefore when all inputs are multiplied by t, output is also multiplied by t. It follows that this production function has constant returns to scale.

You will also be asked to determine whether the marginal product of each single factor of production increases or decreases as you increase the amount of that factor without changing the amount of other factors. Those of you who know calculus will recognize that the marginal product of a factor is the ¯rst derivative of output with respect to the amount of that factor. Therefore the marginal product of a factor will decrease, increase, or stay constant as the amount of the factor increases depending on whether the second derivative of the production function with respect to the amount of that factor is negative, positive, or zero.

Consider the production function f(x1; x2) = x11=2x32=4. The marginal

product of factor 1 is 12 x¡1 1=2x32=4. This is a decreasing function of x1, as you can verify by taking the derivative of the marginal product with respect to x1. Similarly, you can show that the marginal product of x2 decreases as x2 increases.

18.0 Warm Up Exercise. The ¯rst part of this exercise is to calculate marginal products and technical rates of substitution for several frequently encountered production functions. As an example, consider the production function f(x1; x2) = 2x1 + px2. The marginal product of x1 is the derivative of f(x1; x2) with respect to x1, holding x2 ¯xed. This is just 2. The marginal product of x2 is the derivative of f(x1; x2) with

respect to x , holding x ¯xed, which in this case is 1 . The T RS is

2 p 1 2px2

¡MP1=MP2 = ¡4 x2. Those of you who do not know calculus should ¯ll in this table from the answers in the back. The table will be a useful reference for later problems.

Marginal Products and Technical Rates of Substitution

f(x1; x2)				MP1(x1; x2)			MP2(x1; x2)	T RS(x1; x2)
x1 + 2x2
ax1 + bx2
50x1x2
x1=4x3=4				1 x¡3=4x3=4
1	2			4	1	2
Cx1ax2b				Cax1a¡1x2b
(x1 + 2)(x2 + 1)					x2 + 1
(x1 + a)(x2 + b)
ax1 + bp
		x2
xa	+ xa
1	2
(x1a + x2a)b				bax1a¡1 (x1a + x2a)b¡1			bax2a¡1 (x1a + x2a)b¡1

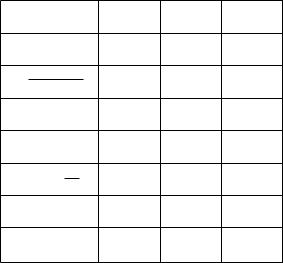
Returns to Scale and Changes in Marginal Products

For each production function in the table below, put an I, C, or D in the ¯rst column if the production function has increasing, constant, or decreasing returns to scale. Put an I, C, or D in the second (third) column, depending on whether the marginal product of factor 1 (factor 2) is increasing, constant, or decreasing, as the amount of that factor alone is varied.

f(x1; x2) Scale MP1 MP2

x1 + 2x2

px1 + 2x2

:2x1x22

x11=4x32=4

x1 + px2

(x1 + 1):5(x2):5

³x11=3 + x12=3´3

18.1 (0) Prunella raises peaches. Where L is the number of units of labor she uses and T is the number of units of land she uses, her output

1 1

is f(L; T ) = L2 T 2 bushels of peaches.

(a) On the graph below, plot some input combinations that give her an output of 4 bushels. Sketch a production isoquant that runs through these points. The points on the isoquant that gives her an output of 4 bushels

all satisfy the equation T =

.