
- •Математика. Алгебра и геометрия
- •Математика. Алгебра и геометрия. Методические указания и контрольные задания для студентов заочной формы обучения./ сост. С.И.Борсуковский, л.А.Тягульская – Рыбница, 2010. – 38с.
- •Задания для контрольных работ Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Задание 11
- •Задание 12
- •Пример выполнения контрольной работы
- •З а д а ч а 2
- •З а д а ч а 4
- •З а д а ч а 5
- •З а д а ч а 6
- •З а д а ч а 7
- •З а д а ч а 8
- •З а д а ч а 9
- •З а д а ч а 10
- •З а д а ч а 11
- •З а д а ч а 12.
- •Список литературы
- •Содержание
- •Математика. Алгебра и геометрия
З а д а ч а 4
Канонические уравнения кривых второго порядка имеют вид
1)
 - эллипс с фокусами
- эллипс с фокусами ,
где
,
где ,
и эксцентриситетом
,
и эксцентриситетом .
Если
.
Если ,
то уравнение
,
то уравнение описывает окружность, в этом случае
описывает окружность, в этом случае ;
;
2)
 - гипербола с фокусами
- гипербола с фокусами ,
где
,
где ,
и эксцентриситетом
,
и эксцентриситетом .
Прямые
.
Прямые являются асимптотами гиперболы;
являются асимптотами гиперболы;
3)
 - парабола, симметричная оси Ох, с фокусом
- парабола, симметричная оси Ох, с фокусом и директрисой
и директрисой ,
, -
парабола, симметричная относительно
Оу, с фокусом
-
парабола, симметричная относительно
Оу, с фокусом и директрисой
и директрисой .
.
Пример 4
Составить уравнение параболы с вершиной в начале координат, если ее директриса параллельна оси Оу и проходит через левый фокус гиперболы:
 .
.
Определим
координаты левого фокуса гиперболы:
 ,
, .
Так как директриса параболы параллельна
оси Оу и проходит через точку
.
Так как директриса параболы параллельна
оси Оу и проходит через точку ,
то она имеет уравнение
,
то она имеет уравнение .
Определим значение параметра р параболы:
.
Определим значение параметра р параболы: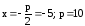 .
Каноническое уравнение параболы имеет
вид
.
Каноническое уравнение параболы имеет
вид ,
т. е.
,
т. е. .
.
З а д а ч а 5
Нормальные
уравнения кривых второго порядка с
центром в точке
 имеют вид
имеют вид
 -
окружность радиусом R;
-
окружность радиусом R;
 -
эллипс с полуосями а и b;
-
эллипс с полуосями а и b;
 -
гипербола;
-
гипербола;
 или
или
 - парабола.
- парабола.
Пример 5
Дано
уравнение линии
 .
Записать уравнение линии в нормальной
форме и построить эту кривую.
.
Записать уравнение линии в нормальной
форме и построить эту кривую.
Чтобы
привести уравнение к нормальной форме,
сгруппируем слагаемые, содержащие
только х и у, вынося коэффициенты при
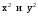 за скобки:
за скобки:
 .
.
Дополняем выражения в скобках до полных квадратов:
 ;
;
 ;
;
 ;
;
 .
.
Разделив обе части на 144, получим нормальное уравнение эллипса:
 с
полуосями
с
полуосями
 с центром в точке
с центром в точке .
Через точку
.
Через точку проведем новые оси координат (
проведем новые оси координат ( и
и )
параллельные соответственно осям Ох и
Оу. По обе стороны от точки
)
параллельные соответственно осям Ох и
Оу. По обе стороны от точки отложим по оси
отложим по оси отрезки длиной
отрезки длиной ,
а по оси
,
а по оси -
- ,
получив таким образом вершины эллипса.
Проведя через вершины вспомогательные
отрезки, параллельные осям, получим
прямоугольник, в который нужно вписать
эллипс. Чертим эллипс.
,
получив таким образом вершины эллипса.
Проведя через вершины вспомогательные
отрезки, параллельные осям, получим
прямоугольник, в который нужно вписать
эллипс. Чертим эллипс.
у




х
О


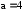



Координаты
фокусов эллипса в новых осях:
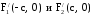 .
Здесь
.
Здесь .
Старыми координатами фокусов будут
.
Старыми координатами фокусов будут
 ,
т. к.
,
т. к. и
и
З а д а ч а 6
Общее
уравнение плоскости имеет вид:
 ,
где
,
где - ненулевой вектор, перпендикулярный
плоскости (нормальный вектор плоскости).
- ненулевой вектор, перпендикулярный
плоскости (нормальный вектор плоскости).
Уравнение
плоскости, проходящей через три данные
точки
 ,
,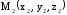 и
и определяется равенством
определяется равенством
 .
.
Расстояние
от точки
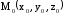 до плоскости
до плоскости находится по формуле
находится по формуле .
.
Пример 6
Найти
расстояние от точки
 до плоскости, проходящей через точки
до плоскости, проходящей через точки .
.
Найдем
уравнение плоскости, проходящей через
точки

 :
:

Вычислим определитель, разложив его по первой строке:


Найдем
расстояние от точки
 до плоскости
до плоскости .
.

