
- •Міністерство освіти і науки України
- •Приклади:
- •§2. Відкриті множини метричних просторів та їх властивості
- •§3. Топологія. Топологічні простори. Приклади
- •§4. Замкнені підмножини топологічного простору
- •§5. Внутрішні точки. Внутрішність підмножини топологічного простору
- •§6. Точки дотику. Замикання підмножин топологічного простору
- •§7. Ізольовані, граничні, межові точки
- •§8. База топологічного простору. Введення топології за допомогою бази
- •§9. Неперервне відображення топологічних просторів. Гомеоморфізми
- •§10. Компактні топологічні простори
- •Список використаної літератури.
§2. Відкриті множини метричних просторів та їх властивості
Нехай
![]() - метричний простір,
- метричний простір,![]() - елемент простору,
- елемент простору,![]() .
.
Множина
![]() називаєтьсявідкритою
кулею з центром у
точці
називаєтьсявідкритою
кулею з центром у
точці
![]() і радіусом
і радіусом![]() .
.
Множина
![]() називаєтьсязамкненою
кулею з центром у
точці
називаєтьсязамкненою
кулею з центром у
точці
![]() і радіусом
і радіусом![]() .
.
Множина
![]() називаєтьсясферою
з центром
називаєтьсясферою
з центром
![]() і радіусом
і радіусом![]() .
.
Множину
![]() називають
називають
![]() -околом
точки
-околом
точки
![]() .
.
В метричному просторі можна
ввести означення відстані між його
підмножинами,а саме, якщо
![]() ,
то
,
то![]() .
.
Означення відстані між
підмножинами дозволяє ввести означення
![]() -околу
підмножини А метричного простору. А
саме, якщо
-околу
підмножини А метричного простору. А
саме, якщо
![]() міститься в М, то
міститься в М, то
![]()
Нехай М - метричний простір,
U – підпростір
простору М, називають відкритою множиною,
якщо або U
– пуста множина, або будь-яка точка з U
входить в U
разом з деяким своїм
![]() -околом.
Тобто
-околом.
Тобто
![]()
Твердження 1: Нехай
М – метричний простір,
![]() ,
тоді:
,
тоді:
Відкрита куля
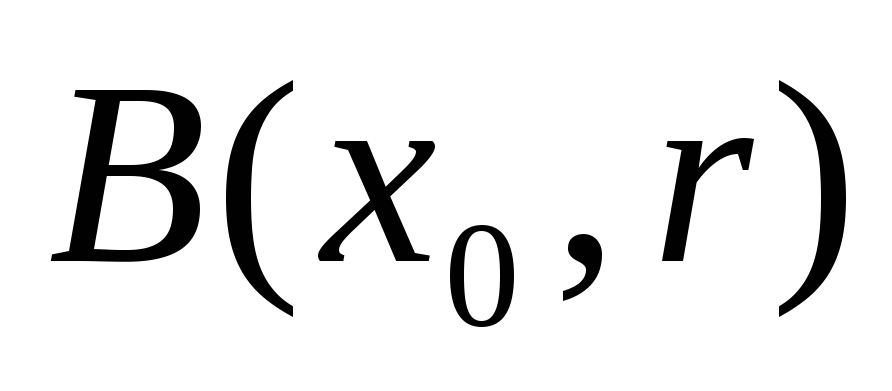 - відкрита множина.
- відкрита множина.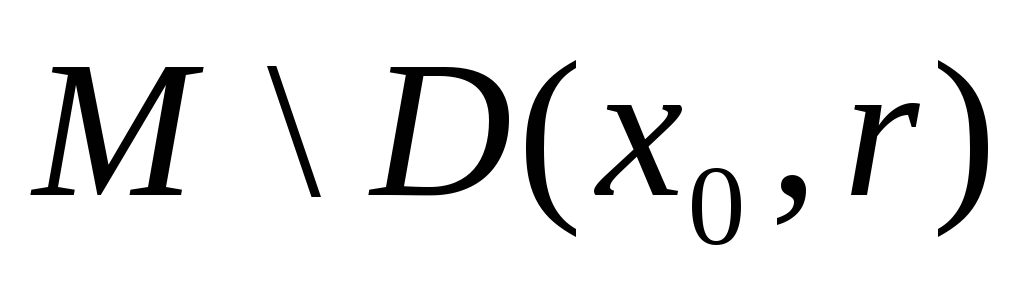 - відкрита множина.
- відкрита множина.
Доведення: Нехай
![]() .
.
Покажемо, що
![]()
Нехай
![]() тоді
тоді
![]()
Таким чином,
![]() .
.
Оскільки
![]() то весь цей окіл належить
то весь цей окіл належить![]()
![]()
![]()
1 пункт доведено.
Нехай
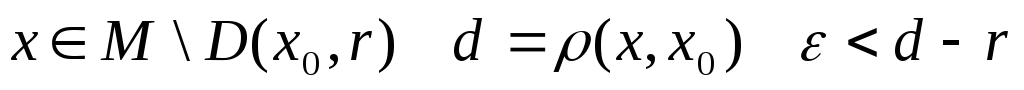
Нехай
![]() тоді за аксіомою трикутника, маємо:
тоді за аксіомою трикутника, маємо:
![]()
Таким чином,
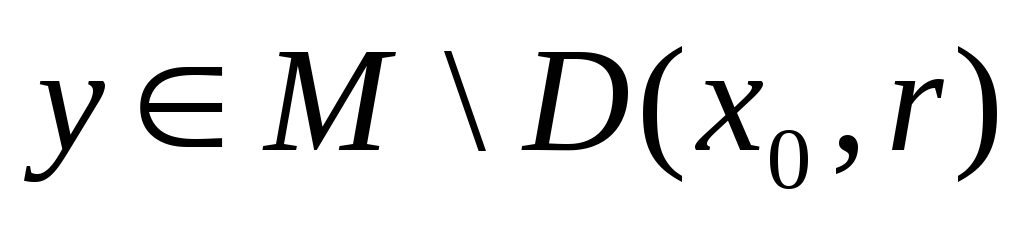
Оскільки
![]() то весь цей окіл належить
то весь цей окіл належить![]()
![]()
![]()
Все доведено.
Теорема 2 (властивості відкритих множин метричного простору):
Нехай М – метричний простір, тоді сукупність усіх відкритих множин простору М задовольняє наступним властивостям:
Пуста підмножина та вся множина М є відкритими.
Об’єднання будь-якої кількості відкритих підмножин простору М є множиною відкритою.
Перетин будь-якої скінченної сукупності відкритих підмножин з М – відкрита множина в М.
Доведення: 1. За означенням відкритої множини пуста множина є відкритою, а будь-яка точка з М входить у простір М з будь-яким своїм околом. Тому М – також відкрита.
Нехай
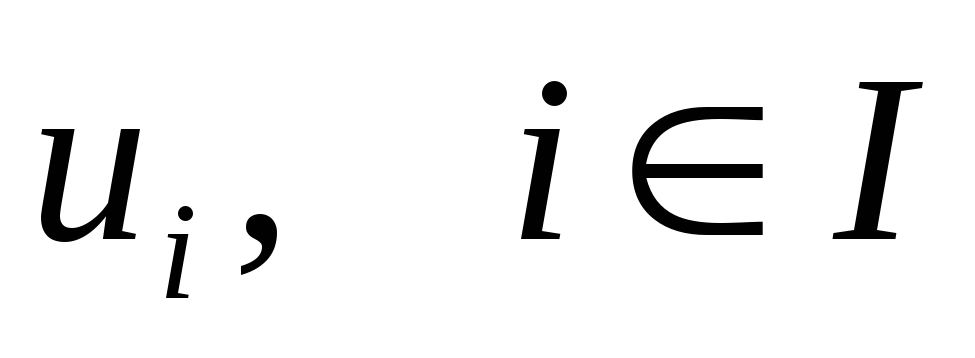 -деяка сукупність відкритих
множин простору М
-деяка сукупність відкритих
множин простору М
![]()
Покажемо, що U – відкрита множина М.
Нехай
![]() ,
тоді
,
тоді![]()
Оскільки
![]() - відкрита, то
- відкрита, то![]()
Але за означенням об’єднання:
![]()
Таким чином,
![]() U– відкрита.
U– відкрита.
Нехай
 за означенням перетину:
за означенням перетину:
![]()
Оскільки підмножини
![]() - відкриті, то
- відкриті, то![]() .
Нехай
.
Нехай
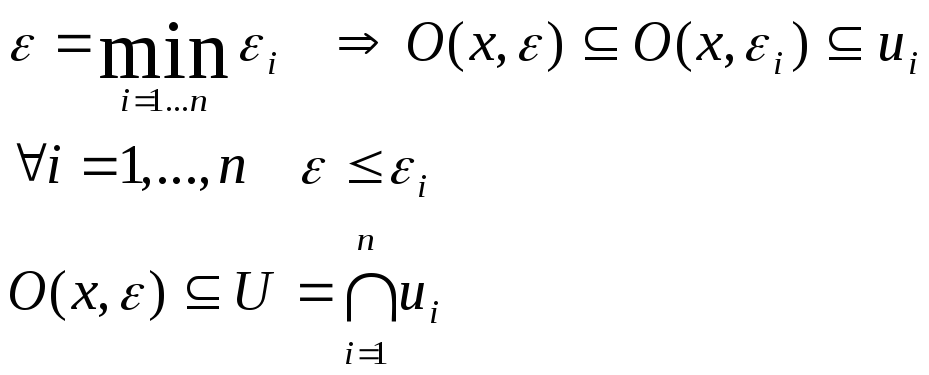
Таким чином, кожна точка U
входить в U
разом з деяким своїм околом
![]() U – відкрита
підмножина.
U – відкрита
підмножина.
Зауваження: Перетин нескінченної сукупності відкритих підмножин метричного простору може бути відкритим.
Розглянемо відкриті підмножини:
![]() не є відкритою підмножиною,
оскільки ніякий окіл числа 1 не попадає
в множину (0,1].
не є відкритою підмножиною,
оскільки ніякий окіл числа 1 не попадає
в множину (0,1].
Твердження 2: Підмножина U множини М є відкритою тоді і тільки тоді, коли U є об’єднанням деякої сукупності відкритих куль з М.
Доведення: Нехай U є об’єднанням деякої сукупності відкритих куль. За твердженням 1 кожна ця куля є відкритою підмножиною, тоді за властивістю 2 попередньої теореми : U – також відкрита підмножина з М.
Нехай U – відкрита підмножина з М, тоді за означенням відкритої підмножини:
![]()
Оскільки
![]() - відкриті кулі, то твердження доведено.
- відкриті кулі, то твердження доведено.
§3. Топологія. Топологічні простори. Приклади
Нехай Т – деяка множина, тоді
булеан
![]() -
сукупність усіх підмножин.
-
сукупність усіх підмножин.
Деяка сукупність
![]() підмножин множини
підмножин множини![]() називаєтьсятопологією
на множині Т, якщо
називаєтьсятопологією
на множині Т, якщо
![]() задовольняє наступним аксіомам (аксіомам
топології)
задовольняє наступним аксіомам (аксіомам
топології)
Т1:
![]() пуста
множина, сама множина Т містяться в
пуста
множина, сама множина Т містяться в![]() .
.
Т2:
![]()
Об’єднання будь-якої сукупності
підмножин з
![]() також належить до
також належить до![]() .
.
Т3:
![]()
Перетин скінченної сукупності
підмножин з
![]() належить до
належить до![]() .
.
Якщо на множині Т задана деяка
топологія
![]() ,
то пару (Т,
,
то пару (Т,![]() )
називаютьтопологічним
простором.
При цьому елементи множини Т називаються
точками цього
простору. А підмножини з
)
називаютьтопологічним
простором.
При цьому елементи множини Т називаються
точками цього
простору. А підмножини з
![]() називаютьсявідкритими
підмножинами з цього
простору.
називаютьсявідкритими
підмножинами з цього
простору.
Якщо заздалегідь невідомо, про яку топологію на Т йде мова, то для позначення топологічного простору можна використовувати лише позначення множини Т.
Приклад 1:
(М,
![]() )
– деякий метричний простір.
)
– деякий метричний простір.
Нехай
![]() - сукупність всіх відкритих підмножин
цього простору. За теоремою
- сукупність всіх відкритих підмножин
цього простору. За теоремою![]() задовольняє всім аксіомам топології,
тоді (М,
задовольняє всім аксіомам топології,
тоді (М,![]() )
є топологічним простором. Цю топологію
)
є топологічним простором. Цю топологію![]() називаютьтопологією
на М, індукованою метрикою
називаютьтопологією
на М, індукованою метрикою
![]() ,
і позначається
,
і позначається
![]() .
.
Таким чином, поняття топологічного простору є деяким узагальненням метричного простору.
Нехай (Т,
![]() )
– деякий топологічний простір. Якщо на
множині Т можна задати метрику
)
– деякий топологічний простір. Якщо на
множині Т можна задати метрику![]() ,
так що (Т,
,
так що (Т,![]() )=(Т,
)=(Т,![]() ),
то кажуть, що топологія
),
то кажуть, що топологія![]() єметризованою.
єметризованою.
Зазначимо, що далеко не всі топології є метризованими.
Приклад 2:
Нехай Т – множина.
![]() =
=![]() ,
тоді
,
тоді![]() - топологія на Т, яку називаютьдискретною.
Зазначимо, що дискретна топологія
індукована дискретною метрикою. У цій
топології усі підмножини з Т є відкритими.
І зокрема, точки дискретного простору
є відкритими підмножинами.
- топологія на Т, яку називаютьдискретною.
Зазначимо, що дискретна топологія
індукована дискретною метрикою. У цій
топології усі підмножини з Т є відкритими.
І зокрема, точки дискретного простору
є відкритими підмножинами.
Приклад 3:
Нехай Т – множина.
![]() ,
,![]() задовольняє всім аксіомам топології.
Цю топологію називаютьтривіальною
топологією на Т.
задовольняє всім аксіомам топології.
Цю топологію називаютьтривіальною
топологією на Т.
Приклад 4: Нехай Т – нескінченна множина, покладемо:
![]()
![]() є топологією на Т, яку називають
топологією скінченних
доповнень (топологією
Заріського).
Перевіримо, що
є топологією на Т, яку називають
топологією скінченних
доповнень (топологією
Заріського).
Перевіримо, що![]() є топологією на Т:
є топологією на Т:
З означення
![]() випливає Т1
випливає Т1
Т2: Нехай
![]()
Розглянемо кількість
![]()
Якщо усі
![]() - пусті підмножини, то
- пусті підмножини, то![]() .
.
Якщо не всі – то їх можна не писати в об’єднання.
Таким чином, можна вважати ,
що всі множини
![]() є не пусті.
є не пусті.
Т3:
![]()
Якщо хоча б одна з множин
![]() пуста, то
пуста, то![]() також пуста з
також пуста з![]() .
.
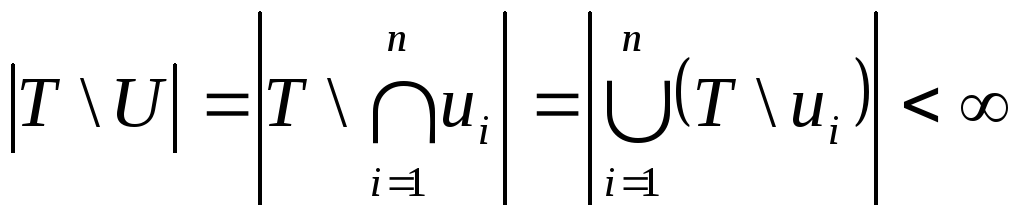
![]()
Приклад 5:
Нехай (Т,
![]() )
– топологічний простір і нехай
)
– топологічний простір і нехай
![]()
Покажемо, що
![]() є топологією на множиніА.
є топологією на множиніА.
Т1:
![]()
Т2:
![]()
![]()
Т3: Нехай
![]()
Таким чином,
![]() - топологія на підмножині А, яку називають
топологією, індукованою на А топологією
- топологія на підмножині А, яку називають
топологією, індукованою на А топологією![]() називають підгрупою простору
називають підгрупою простору![]() .
.
Таким чином, всяку підмножину простору Т можна розглядати як його підпростір з індукованою топологією.
Якщо
![]() ,
то
,
то![]() - слабкіша,
- слабкіша,![]() - сильніша. Найслабкіша – тривіальна
- сильніша. Найслабкіша – тривіальна![]() ,
найсильніша – дискретна
,
найсильніша – дискретна![]()
