
- •Міністерство освіти і науки України
- •Приклади:
- •§2. Відкриті множини метричних просторів та їх властивості
- •§3. Топологія. Топологічні простори. Приклади
- •§4. Замкнені підмножини топологічного простору
- •§5. Внутрішні точки. Внутрішність підмножини топологічного простору
- •§6. Точки дотику. Замикання підмножин топологічного простору
- •§7. Ізольовані, граничні, межові точки
- •§8. База топологічного простору. Введення топології за допомогою бази
- •§9. Неперервне відображення топологічних просторів. Гомеоморфізми
- •§10. Компактні топологічні простори
- •Список використаної літератури.
§8. База топологічного простору. Введення топології за допомогою бази
Нехай
![]() - топологічний простір,
- топологічний простір,![]() - його топологія.
- його топологія.![]() називаєтьсябазою
топології
називаєтьсябазою
топології
![]() ,
якщо будь-яка підмножина з
,
якщо будь-яка підмножина з![]() є об’єднанням деякої сукупності
підмножин з
є об’єднанням деякої сукупності
підмножин з![]() (при цьому вважається, що
(при цьому вважається, що![]() є об’єднанням пустої сукупності
підмножин з
є об’єднанням пустої сукупності
підмножин з![]() ).
).
Твердження 1 (критерій бази):
![]() - топологічний простір.
- топологічний простір.![]() є базою топології
є базою топології![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли![]()
Доведення:
Припустимо, що
![]() - база топології
- база топології![]() .
Виберемо довільну точку
.
Виберемо довільну точку![]() і деякий її окіл
і деякий її окіл![]() .
Оскільки
.
Оскільки![]() є відкритою множиною, то він є об’єднанням
деякої сукупності підмножин
є відкритою множиною, то він є об’єднанням
деякої сукупності підмножин![]() .
Оскільки
.
Оскільки![]() ,
то з означення об’єднання випливає, що
,
то з означення об’єднання випливає, що![]() .
.
Припустимо тепер, що
![]() задовольняє умові критерію, і покажемо,
що тоді
задовольняє умові критерію, і покажемо,
що тоді![]() - база топології
- база топології![]() ,
тобто будь-яка відкрита підмножина
,
тобто будь-яка відкрита підмножина![]() є об’єднанням деякої сукупності
підмножин з
є об’єднанням деякої сукупності
підмножин з![]() .
.
Дійсно, оскільки
![]() - відкрита, то
- відкрита, то![]() .
Тоді за умовою критерію:
.
Тоді за умовою критерію:
![]() .
Все доведено.
.
Все доведено.
Приклади:
1. З
розділу “Відкриті підмножини метричного
простору ” випливає, що
![]() утворює базу індукованої топології
утворює базу індукованої топології![]() .
Оскільки будь-яка відкрита підмножина
з М є об’єднанням деякою сукупності
відкритих куль. Але ця топологія має і
меншу базу:
.
Оскільки будь-яка відкрита підмножина
з М є об’єднанням деякою сукупності
відкритих куль. Але ця топологія має і
меншу базу:![]() .
.
В природній топології числової прямої R базу утворюють усі обмежені відкриті інтервали
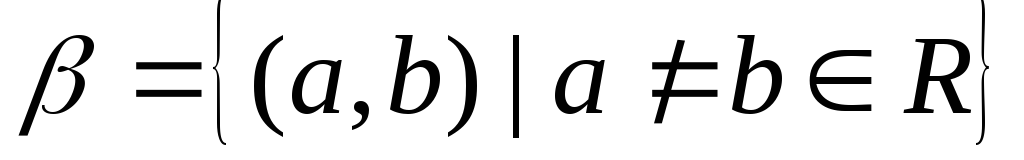 .
Відзначимо, що хоча ця топологія наR
має потужність контінум, але вона має
зліченну базу
.
Відзначимо, що хоча ця топологія наR
має потужність контінум, але вона має
зліченну базу
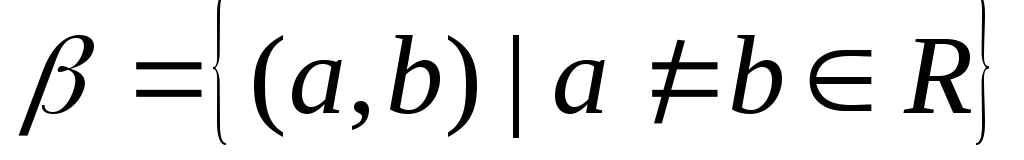 ,
що випливає з критерію бази.
,
що випливає з критерію бази.
Твердження 2 (необхідна
умова бази): Нехай
![]() - топологічний простір. Якщо
- топологічний простір. Якщо![]() є базою топології
є базою топології![]() ,
то
,
то![]() задовольняє наступним умовам:
задовольняє наступним умовам:
1.
![]()
2.
![]()
Доведення: 1.
Оскільки Т – відкрита множина, то Т
можна представити як об’єднання
елементів бази
![]() .
За означенням об’єднання
.
За означенням об’єднання
![]() .
.
Нехай
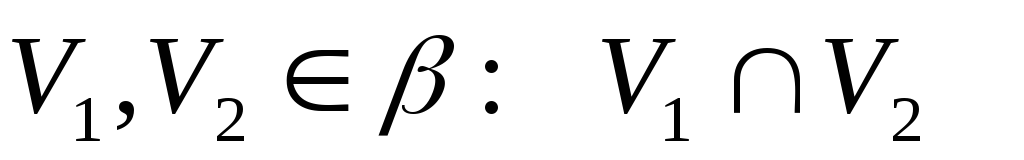 -
відкрита множина, як перетин двох
відкритих множин.
-
відкрита множина, як перетин двох
відкритих множин.
![]() - окіл точки х
і за критерієм бази
- окіл точки х
і за критерієм бази
![]() .
Все доведено.
.
Все доведено.
Теорема( про введення
топології за допомогою бази): Нехай
Т – деяка множина і
![]() .
Припустимо, що
.
Припустимо, що![]() задовольняє умовам 1) і 2) попереднього
твердження, тоді існує єдина топологія
задовольняє умовам 1) і 2) попереднього
твердження, тоді існує єдина топологія![]() на Т, для якої
на Т, для якої![]() є базою.
є базою.
Доведення:
Нехай
![]() - сукупність усіх можливих об’єднань
підмножин з
- сукупність усіх можливих об’єднань
підмножин з
![]() .
Перевіримо аксіоми топології для
.
Перевіримо аксіоми топології для![]() :
:
Т1: З умови 1) попереднього
твердження випливає, що Т є об’єднання
деякої сукупності підмножин з
![]() .
Таким чином,
.
Таким чином,![]() .
.
Пусту множину можна розглядати
як об’єднання пустої сукупності
підмножин з
![]() ,
тому
,
тому![]()
![]() .
.
Т2 – виконується, оскільки
об’єднання будь-якої сукупності
об’єднань підмножин з
![]() буде об’єднанням підмножин з
буде об’єднанням підмножин з![]() ,
тому
,
тому![]() потрапляє в
потрапляє в![]() .
.
Т3: Для доведення цієї аксіоми застосуємо метод математичної індукції:
а) Нехай
![]() .
.
Покажемо, що
![]() .
.
Дійсно,
![]() .
.
Достатньо показати, що
![]() ,
тоді з аксіоми Т2 випливає, що
,
тоді з аксіоми Т2 випливає, що![]() .
.
Згідно умові 2) попереднього твердження:
![]()
Тоді цей перетин є
![]()
б) Припустимо, що перетин
будь-якої k
підмножин з
![]() належить
належить![]() .
Покажемо, що перетин k+1
підмножин з
.
Покажемо, що перетин k+1
підмножин з
![]() також належить
також належить![]() :
:
![]() .
Все доведено.
.
Все доведено.
§9. Неперервне відображення топологічних просторів. Гомеоморфізми
Нехай X,
Y -
топологічні простори. Відображення
![]() називаєтьсянеперервним
в точці
називаєтьсянеперервним
в точці
![]() ,
якщо
,
якщо
![]() .
.
Якщо відображення
![]() - неперервне в
- неперервне в![]() ,
то воно називаєтьсянеперервним
відображенням топологічних просторів.
,
то воно називаєтьсянеперервним
відображенням топологічних просторів.
Нехай
![]() - деяка база просторуХ,
- деяка база просторуХ,
![]() - деяка база просторуY.
Означення неперервності відображення
можна ввести , використовуючи тільки
елементи баз цих просторів, а саме:
- деяка база просторуY.
Означення неперервності відображення
можна ввести , використовуючи тільки
елементи баз цих просторів, а саме:
Твердження 1:
Нехай X, Y
- топологічні простори,
![]() ,
,![]() - їх бази. Відображення
- їх бази. Відображення![]() буде неперервним в
буде неперервним в![]() тоді і тільки тоді, коли
тоді і тільки тоді, коли
![]()
Доведення:
Припустимо, що
![]() - неперервне в точціх.
Виберемо
- неперервне в точціх.
Виберемо
![]()
Оскільки
![]() - окіл точкиу,
то за означенням неперервності
- окіл точкиу,
то за означенням неперервності
![]() .
.
За критерієм бази
![]() .
.
Припустимо тепер, що відображення
![]() задовольняє умову твердження, тобто
відображення – неперервне:
задовольняє умову твердження, тобто
відображення – неперервне:
![]() .
.
За умовою твердження:
![]()
Оскільки
![]() є околом точких,
то
є околом точких,
то
![]() .
Все доведено.
.
Все доведено.
Розглянемо тепер неперервні відображення метричних просторів.
Оскільки сукупність усіх
![]() -околів
метричного простору утворює базу його
топології, то можна ввести наступні
означення неперервності відображень
метричних просторів.
-околів
метричного простору утворює базу його
топології, то можна ввести наступні
означення неперервності відображень
метричних просторів.
Нехай X,
Y -
метричні простори,
![]() ,
,![]() .Відображення
.Відображення
![]() називаєтьсянеперервним
в точці х,
якщо:
називаєтьсянеперервним
в точці х,
якщо:
![]() .
.
Оскільки
![]() і
і![]() є елементами бази просторівX,
Y ,
то згідно твердження 1, це означає
еквівалентне означенню неперервності
відображення топологічних просторів.
В окремому випадку числових функцій
(функцій, заданих на просторіR)
означення неперервності має наступний
вигляд:
є елементами бази просторівX,
Y ,
то згідно твердження 1, це означає
еквівалентне означенню неперервності
відображення топологічних просторів.
В окремому випадку числових функцій
(функцій, заданих на просторіR)
означення неперервності має наступний
вигляд:
![]()
Функція f
неперервна в точці
![]() ,
якщо:
,
якщо:![]()
Твердження 2 (критерій неперервності відображень топологічних просторів):
Нехай X,
Y -
топологічні простори,
![]() неперервне тоді і тільки тоді, коли :
неперервне тоді і тільки тоді, коли :
Прообраз будь-якої відкритої множини з Y є відкритою множиною в X.
Прообраз будь-якої замкненої множини з Y є замкненою множиною в X.
Доведення:
1.
Припустимо, що
![]() є неперервним. НехайU–довільна відкрита множина
з Y.
Покажемо, що
є неперервним. НехайU–довільна відкрита множина
з Y.
Покажемо, що
![]() є відкритою множиною вX.
є відкритою множиною вX.
Нехай
![]() ,
тодіU
можна розглядати як деякий окіл точки
у і за
означенням неперервності відображення
,
тодіU
можна розглядати як деякий окіл точки
у і за
означенням неперервності відображення
![]() .
.
Довільний х
входить в V
разом з деяким своїм околом
![]()
![]() є відкритою.
є відкритою.
Припустимо тепер, що
відображення
![]() задовольняє умові твердження, тобто
прообраз будь-якої відкритої множини
зY є
відкритою множиною в X.
задовольняє умові твердження, тобто
прообраз будь-якої відкритої множини
зY є
відкритою множиною в X.
Покажемо, що
![]() є неперервним,
є неперервним,
![]() ,
,![]() .
.
Нехай
![]() - деякий окіл точкиу.
Оскільки
- деякий окіл точкиу.
Оскільки
![]() - відкрита множина, то, згідно умові
твердження, її прообраз
- відкрита множина, то, згідно умові
твердження, її прообраз![]() є відкрита множина вX.
Оскільки
є відкрита множина вX.
Оскільки
![]() ,
то
,
то![]() є околом точких.
є околом точких.
![]()
З означення неперервності 1) умова доведена.
2. Це
твердження випливає з твердження 1 і
рівності
 .
Припустимо, що прообраз будь-якої
замкненої множини зY
є замкненою множиною в X.
Нехай V
– довільна відкрита множина з Y,
тоді
.
Припустимо, що прообраз будь-якої
замкненої множини зY
є замкненою множиною в X.
Нехай V
– довільна відкрита множина з Y,
тоді
![]() - деяка замкнена множина. Оскільки
- деяка замкнена множина. Оскільки![]() - замкнена множина вX,
то з рівності
- замкнена множина вX,
то з рівності
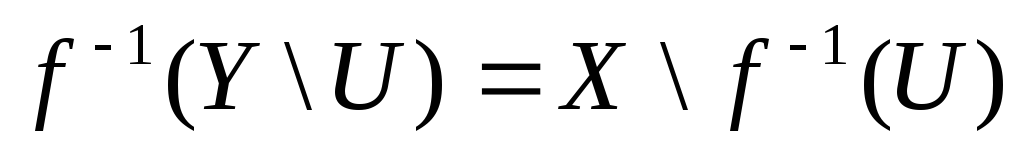 випливає, що
випливає, що![]() - відкрита множина вX.
Прообраз будь-якої відкритої множини
з Y є
відкритою множиною в X.,
тому
- відкрита множина вX.
Прообраз будь-якої відкритої множини
з Y є
відкритою множиною в X.,
тому
![]() - неперервне відображення. Припустимо
тепер, що
- неперервне відображення. Припустимо
тепер, що
![]() - неперервне відображення,
тоді з п.1) випливає, що прообраз будь-якої
відкритої множини з Y
є відкритою множиною
в X.
- неперервне відображення,
тоді з п.1) випливає, що прообраз будь-якої
відкритої множини з Y
є відкритою множиною
в X.
Нехай V
– деяка замкнена множина з Y,
тоді
![]() деU–деяка
відкрита множина з Y
. Оскільки
деU–деяка
відкрита множина з Y
. Оскільки
![]() - відкрита множина вX,
то з рівності
- відкрита множина вX,
то з рівності
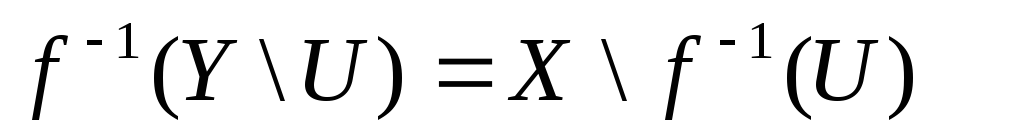 випливає,
що
випливає,
що![]() замкнена множина вX.
замкнена множина вX.
Отже, все доведено.
Твердження 3:
Композиція (суперпозиція) неперервних
відображень топологічних просторів є
неперервним відображенням, тобто, якщо
X, Y,
Z –
топологічні простори,
![]() і
і![]() -
їх неперервні відображення, то
-
їх неперервні відображення, то![]() є неперервним відображенням топологічних
просторів.
є неперервним відображенням топологічних
просторів.
Доведення: Застосуємо критерій з попереднього твердження:
Нехай U
– довільна відкрита
множина з Z,
оскільки прообраз U
такий що:
![]() іf,
g –
неперервні відображення, то згідно
попереднього твердження множина
іf,
g –
неперервні відображення, то згідно
попереднього твердження множина
![]() - відкрита вX,
а
- відкрита вX,
а
![]() є неперервним. І все доведено.
є неперервним. І все доведено.
Нехай X,
Y –
топологічні простори. Відображення
![]() називаєтьсягомеоморфізмом,
якщо f
– бієктивне, неперервне і зворотне до
нього відображення.
називаєтьсягомеоморфізмом,
якщо f
– бієктивне, неперервне і зворотне до
нього відображення.
![]() також є неперервним.
також є неперервним.
Якщо між просторами X
та Y
існує гомеоморфізм, то такі простори
називаються гомеоморфними
і позначаються так:
![]() .
.
Нехай X,
Y –
топологічні простори. Відображення
![]() називається:
називається:
відкритим, якщо образ будь-якої відкритої множини
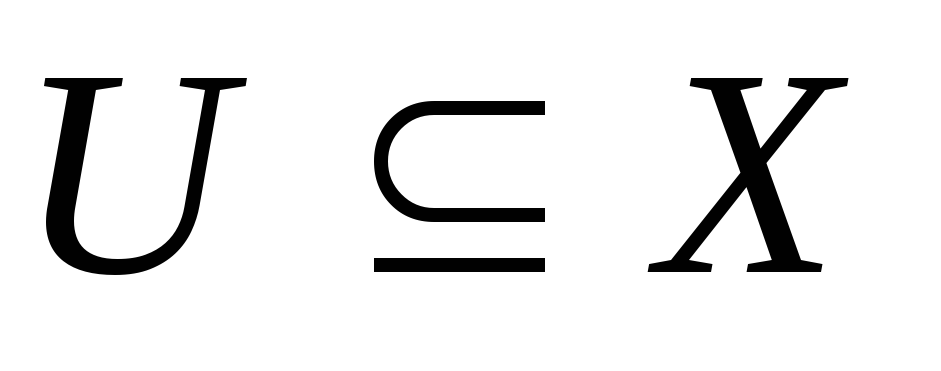 є відкритою множиною вY.
є відкритою множиною вY.замкненим, якщо образ
 будь-якої замкненої множини зX
є замкненою множиною в Y.
будь-якої замкненої множини зX
є замкненою множиною в Y.
Твердження 4:
Нехай X,
Y –
топологічні простори, бієктивне
неперервне відображення
![]() є гомеоморфізмом тоді і тільки тоді,
коли воно є відкритим (замкненим).
є гомеоморфізмом тоді і тільки тоді,
коли воно є відкритим (замкненим).
Доведення:
Доведемо твердження для відкритих
відображень. Для цього застосуємо
критерій (1) з твердження 3. Припустимо,
що f –
гомеоморфізм, і покажемо, що f
– відкрите відображення. Оскільки
f –
гомеоморфізм, то
![]() є неперервним. Покажемо, щоf(U)
-відкрита множина в Y.
Оскільки
є неперервним. Покажемо, щоf(U)
-відкрита множина в Y.
Оскільки
![]() - неперервне відображення іf(U)
– прообраз множини U
при дії неперервного відображення
- неперервне відображення іf(U)
– прообраз множини U
при дії неперервного відображення
![]() ,
то згідно твердження 3f(U)
– відкрита множина в Y.
,
то згідно твердження 3f(U)
– відкрита множина в Y.
Припустимо тепер, що
відображення f
– відкрите і покажемо, що f
– гомеоморфізм. Для цього достатньо
показати, що зворотне відображення
![]() є неперервним.
є неперервним.
Нехай U
– деяка довільна відкрита множина з X,
тоді f(U)
є прообразом множини U
при дії відображення
![]() ,
а оскільки відображенняf
– відкрите, то множина f(U)
є відкритою множиною в Y.
,
а оскільки відображенняf
– відкрите, то множина f(U)
є відкритою множиною в Y.
Таким чином, згідно критерію
1 твердження 3 відображення
![]() є неперервним.
є неперервним.
Для замкнених відображень твердження доводиться аналогічно, замість критерію 1 треба застосувати критерій 2.
Наслідок:
Якщо між топологічними просторами
X, Y
існує гомеоморфізм
![]() ,
то для довільної множини
,
то для довільної множини![]() виконуються співвідношення:
виконуються співвідношення:
1.
![]()
2.
![]()
3.
![]()
Якщо між топологічними просторами існує гомеоморфізм, то вони мають однакові топологічні властивості. У загальній топології гомеоморфні простори вважаються однаковими.
Твердження 5: Гомеоморфність є співвідношенням еквівалентності на класі усіх топологічних просторів, тобто:
1.
![]()
2.
![]()
3.
![]()
Доведення: 1.
Якщо
![]() , то гомеоморфізм
, то гомеоморфізм![]() встановлює тотожне відображення.
встановлює тотожне відображення.
2 . Якщо
![]() - гомеоморфізм, то
- гомеоморфізм, то![]() також гомеоморфізм.
також гомеоморфізм.
3. Нехай
![]() - гомеоморфізм,
- гомеоморфізм,![]() - теж гомеоморфізм, оскільки композиція
бієктивного відображення є бієктивним
відображенням, композиція неперервного
відображення є неперервним відображенням,
зворотне до композиції
- теж гомеоморфізм, оскільки композиція
бієктивного відображення є бієктивним
відображенням, композиція неперервного
відображення є неперервним відображенням,
зворотне до композиції![]() є
є![]() ,
то відображення
,
то відображення![]() - неперервне, а відображення
- неперервне, а відображення![]() - гомеоморфізм. І все доведено.
- гомеоморфізм. І все доведено.
Сукупність усіх топологічних просторів розпадається на класи гомеоморфних просторів і вони не перетинаються. Ці класи називаються топологічними типами. Гомеоморфні простори мають однакові топологічні типи.
