
- •Міністерство освіти і науки України
- •Приклади:
- •§2. Відкриті множини метричних просторів та їх властивості
- •§3. Топологія. Топологічні простори. Приклади
- •§4. Замкнені підмножини топологічного простору
- •§5. Внутрішні точки. Внутрішність підмножини топологічного простору
- •§6. Точки дотику. Замикання підмножин топологічного простору
- •§7. Ізольовані, граничні, межові точки
- •§8. База топологічного простору. Введення топології за допомогою бази
- •§9. Неперервне відображення топологічних просторів. Гомеоморфізми
- •§10. Компактні топологічні простори
- •Список використаної літератури.
§10. Компактні топологічні простори
Нехай X
– топологічний простір. Деяка сукупність
підмножин
![]() називаєтьсяпокриттям
простору X,
якщо
називаєтьсяпокриттям
простору X,
якщо
![]() .
.
Якщо
![]() ,
то система підмножин
,
то система підмножин![]() називаєтьсяпокриттям
множини А,
якщо
називаєтьсяпокриттям
множини А,
якщо
![]() .
.
Якщо всі
![]() - відкриті, то покриття називаєтьсявідкритим.
Підпокриттям
називається деяка сукупність множин з
покриття. Топологічний простір X
називається компактним,
якщо з будь-якого відкритого його
покриття можна виділити скінченне
підпокриття.
- відкриті, то покриття називаєтьсявідкритим.
Підпокриттям
називається деяка сукупність множин з
покриття. Топологічний простір X
називається компактним,
якщо з будь-якого відкритого його
покриття можна виділити скінченне
підпокриття.
Приклади:
Числова пряма не є компактним простором, оскільки з його покриття інтервали вигляду
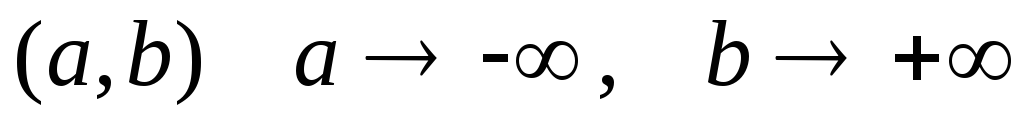 неможливо виділити скінченне підпокриття.
неможливо виділити скінченне підпокриття.Скінченний відкритий інтервал (0, 2) не є компактним простором, оскільки з його покриття інтервали вигляду
 неможливо виділити скінченне підпокриття.
неможливо виділити скінченне підпокриття.Замкнений інтервал
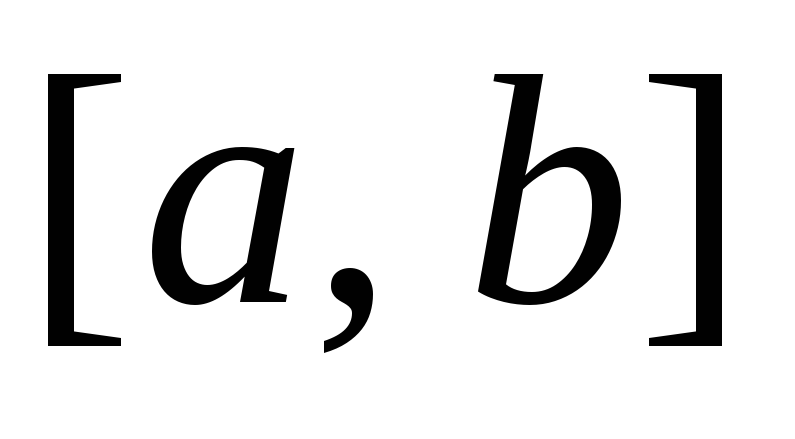 є компактним простором, що доводиться
в лемі Гейне-Бореля.
є компактним простором, що доводиться
в лемі Гейне-Бореля.
Нехай Х – деяка множина,
![]() - деяка система підмножин з множини Х.
- деяка система підмножин з множини Х.![]() називаєтьсяцентрованою,
коли кожна скінченна підсистема підмножин
з
називаєтьсяцентрованою,
коли кожна скінченна підсистема підмножин
з
![]() має непустий перетин.
має непустий перетин.
Твердження 1 (критерій компактності простору):
Топологічний простір Х є компактним тоді і тільки тоді, коли кожна центрована система його замкнених підмножин має непустий перетин.
Доведення:
Припустимо, що простір Х – компактний
і в ньому існує центрована система
замкнених підмножин
![]() ,
яка має пустий перетин, тобто
,
яка має пустий перетин, тобто![]() ,
тоді простір
,
тоді простір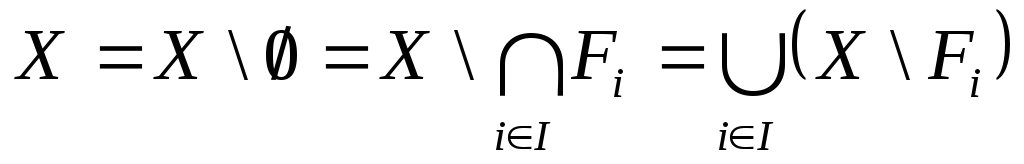 .
Оскільки
.
Оскільки![]() - замкнені, то
- замкнені, то![]() - відкриті, а з рівності
- відкриті, а з рівності![]() випливає, що підмножини
випливає, що підмножини![]() утворюють відкрите покриття простору
Х.
утворюють відкрите покриття простору
Х.
Оскільки простір – компактний,
то це покриття містить скінченне
підпокриття, тобто існують підмножини
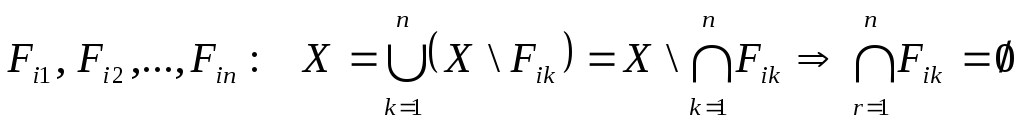 ,
а це протирічить тому, що система
,
а це протирічить тому, що система![]() є центрованою.
є центрованою.
Припустимо,що простір Х
задовольняє умову критерію і покажемо,
що Х є компактним. Нехай
![]() - деяке відкрите покриття простору Х,
тобто
- деяке відкрите покриття простору Х,
тобто![]() ,
тоді
,
тоді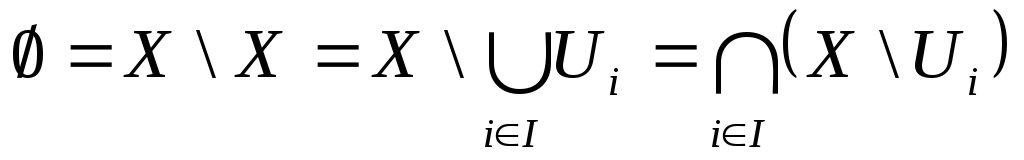 .
Оскільки
.
Оскільки![]() - відкриті, то
- відкриті, то![]() - замкнені. А оскільки
- замкнені. А оскільки![]() ,
то згідно умові критерію
,
то згідно умові критерію![]() не може бути центрованою. Тоді існує
скінченна сукупність підмножин
не може бути центрованою. Тоді існує
скінченна сукупність підмножин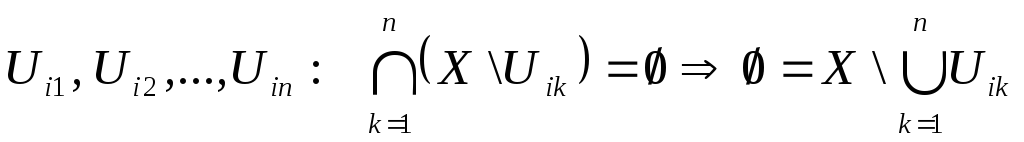 ,
тобто
,
тобто![]() підмножини
підмножини![]() утворюють скінченне відкрите підпокриття
простору Х. Х є компактним. Що і треба
було довести.
утворюють скінченне відкрите підпокриття
простору Х. Х є компактним. Що і треба
було довести.
Підмножина А топологічного
простору Х називається компактною,
якщо підпростір
![]() є компактним.
є компактним.
Твердження 2: Підмножина А топологічного простору Х є компактною тоді і тільки тоді, коли з кожного покриття множини А відкритими в Х підмножинами можна виділити скінченне підпокриття.
Доведення:
Припустимо, що підмножина А є компактною.
Нехай
![]() - деяке покриття множини А відкритими
в просторі Х підмножинами, тобто
- деяке покриття множини А відкритими
в просторі Х підмножинами, тобто![]() - відкриті. Тоді
- відкриті. Тоді![]()
За означенням
![]() :
:![]()
Таким чином, підмножина
![]() утворює відкрите покриття підпростору
утворює відкрите покриття підпростору![]() .
.
Оскільки множина А – компактна,
то і
![]() - компактний, і значить з його відкритого
покриття можна виділити скінченне
підпокриття:
- компактний, і значить з його відкритого
покриття можна виділити скінченне
підпокриття:![]() утворюють скінченне підпокриття
множини А відкритими у просторі Х
підмножинами, тобто А задовольняє умовам
твердження.
утворюють скінченне підпокриття
множини А відкритими у просторі Х
підмножинами, тобто А задовольняє умовам
твердження.
Навпаки: припустимо тепер, що А задовольняє умову твердження, тобто покажемо, що А – компактна.
Нехай
![]() - довільне покриття відкритими підмножинами
простору
- довільне покриття відкритими підмножинами
простору![]() ,
тобто
,
тобто![]() .
За означенням
.
За означенням![]()
Таким чином,
![]() утворюють покриття множини А відкритими
в Х підмножинами. За умовою твердження
з цього покриття можна виділити скінченне
підпокриття, тобто
утворюють покриття множини А відкритими
в Х підмножинами. За умовою твердження
з цього покриття можна виділити скінченне
підпокриття, тобто![]() утворюють скінченне відкрите підпокриття
підпростору
утворюють скінченне відкрите підпокриття
підпростору![]() .
.![]() - компактний, а А – компактна в Х. Все
доведено.
- компактний, а А – компактна в Х. Все
доведено.
Твердження 3: Всяка замкнена підмножина А топологічного простору Х є компактною множиною цього простору.
Доведення:
За означенням компактної множини, нам
треба довести, що підпростір
![]() є компактним. Нехай
є компактним. Нехай![]() - деяка центрована система замкнених в
просторі
- деяка центрована система замкнених в
просторі![]() підмножин. За властивістю замкнених
підмножин підпростору
підмножин. За властивістю замкнених
підмножин підпростору![]() .
.
А оскільки підмножина А також
замкнена в усьому просторі Х, то
![]() показує, що підмножини
показує, що підмножини![]() - замкнені в просторі Х.
- замкнені в просторі Х.![]() є і центрованою системою підмножин
замкнених в просторі Х. Оскільки Х є
компактним, ця система має непустий
перетин. Отже, ми довели, що довільна
центрована система
є і центрованою системою підмножин
замкнених в просторі Х. Оскільки Х є
компактним, ця система має непустий
перетин. Отже, ми довели, що довільна
центрована система![]() замкнених підмножин підпростору
замкнених підмножин підпростору![]() має непустий перетин. За твердженням 1
цей підпростір є компактним. І все
доведено.
має непустий перетин. За твердженням 1
цей підпростір є компактним. І все
доведено.
