17. Обчислення подвійних інтегралів. Приклади.

ОЗНАЧ: область назив правильною у напрямі осі ОУ, якщо довільна пряма, яка проходить через внутрішню точку областіD паралельно осі ОУ перетинає межу області D у двох точках. Аналогічно визначається область правильна у напрямі осі ОХ. Розглянемо випадки:

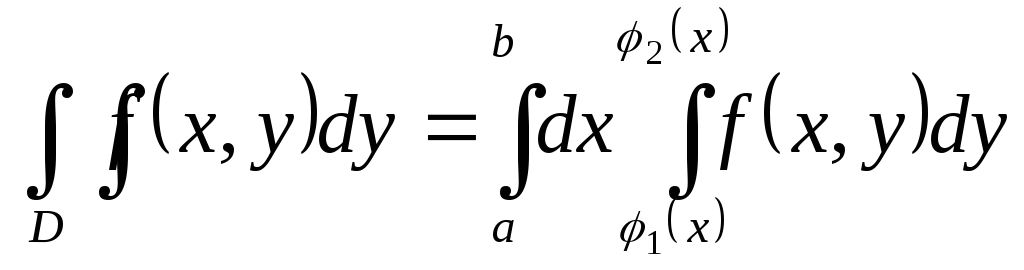1) Нехай область D правильна у напрямі осі ОУ і задається умовами,. Тоді(1)

У формулі (1) спочатку треба обчислити завжди внутрішній інтеграл, а лише потім зовнішній. Межі інтегрування у внутрішн інтегралі можуть бути як змінними, так і сталими величинами. Межі інтегрування у зовн інтегралі завжди сталі. Зазначимо, якщо межі ітегр у внутр інтегралі є змінні, то вони залежать від змінної, що не є змінною інтегр у внутр інтегралі. Якщо всі межі інтегр у внутр інтегралі сталі, то зрозуміло, що область D є прямокутник.

2) Нехай область D правильна у напрямі осі ОХ і визначається умовами,.Тоді (2)

Зауваження. 1) Якщо область D правильна, як у напрямі ОХ, так і у напрямі ОУ, то подвійний інтеграл від функції f(x,y) по області D можна буде обчислити, як за форм (1) так і за (2). Результат повинен бути однаковий.

2)Якщо область інтегр D не є правильн ні у напрямі осі ОХ, ні у напрямі ОУ, то її треба розбити на частини, кожна з яких є правильною областю. Обчислюючи інтеграли по одержаним областям і додаючи їх за властивістю 5 подвійного інтегралу, одержимо шуканий інтеграл по області D.

3)Якщо виявляється, що нижня або верхня межа області D складається з кривих, що задаються різними рівняннями область D необхідно розбити на частини так, щоб кожна з ліній одержан частин визначалась лише одним рівнянням .Тоді подвійний інтеграл

₊

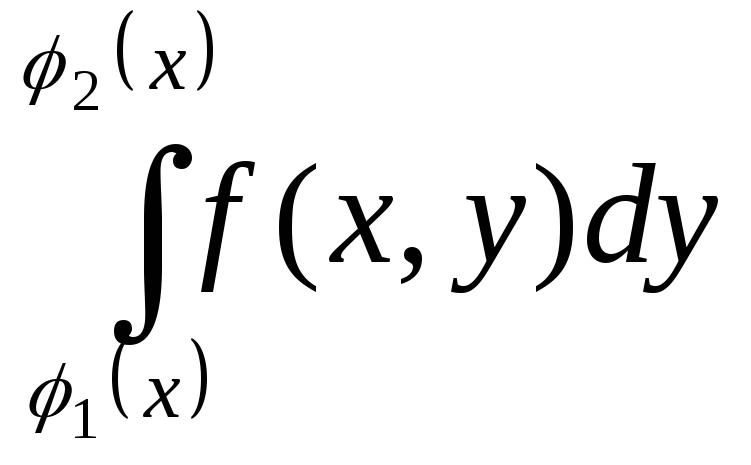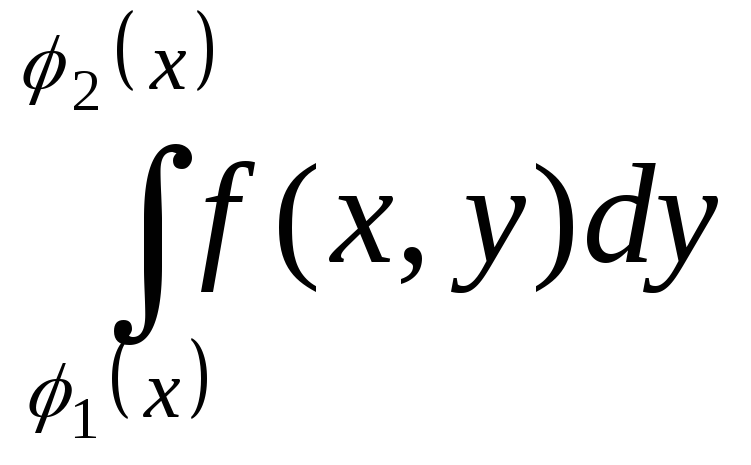
Тоді .₊

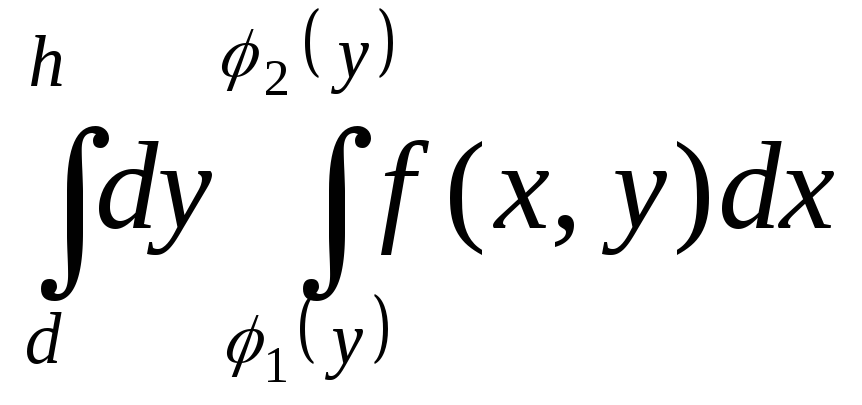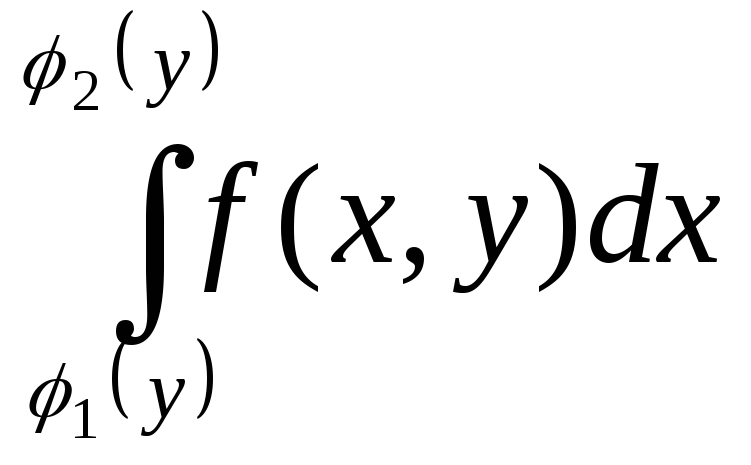
18. Заміна змінних в подвійному інтегралі.Подвійний інтеграл у полярних координатах.

Нехай функція f(x,y) визначена у замкненій обмеж ній області D що належить /R у квадраті, зробимо у області D у подвін. Інтегр. SS по D f(x,y) dxdy перехід до нових змінних U i V за формулами дельта X =X(U,V) y=y(U,V) (1)Будемо вважати, що функції 1 непреривні і з формули 1 однозначно визначаються функц. U =U(X,Y) V=V(x,y) (2)

Тоді в кожній точці M(x,y)Є D відповідає деяка точка з M з зірочкою (U,V). Множина всіх точок M з зірочкою утворює замкнену обмежину область D з зірочкою.

Означ. Формули (1) назив. Формул. Перетвор. Координат, а формули (2) формулами оберненного перетворення

Теорема. Якщо перетвор (2) перевод. Замкнену обмежину D з зірочкою і функц. (1) мають в області D з зірочкою неперервність частинні похідні і відмінні від о визначник J(U,V)= ” ”(3) а функція f(x,y) неперервна в області D те справедлива формула SSпо D f(x,y)dxdy= SS по D f(x(U,V),y(U,V))*|J(U,V)|dudv(4)

Означ.Функц. означн. (3) назив визначн. Якобі, або, Якобіаним. Таким чином викон. Заміну змінних у інтегралі Sпо D f(x,y)dxdy за формул. (1) потрібно Елемент площі dxdy в координатах (x,y) замінити на елементи площі |J(U,V)|dudv в координатах (U,V) і перейти від старої області D до відповідно її абр. D з зірочкою.

Розглянемо заміну декарт. Кордин. (x,y) полярн. Координ. ро ,фі.За відомими формулами Y=роsinфі X=роcosфі, тоді визначник якобі J(ро ,фі) =” ”= Y=роcos*cosфі X=роsin*sinфі=ро.Таким чином подвійницй інтеграл SSпо D f(x,y)dxdy= SSпо Dx f(роcosфі, роsinфі) роdpdфі(5). Де D з зірочкою об. В полярних координатах (X,Y).

Зауваж: 1)У богат. Випадках формулу (5) доцільно застосов. Тоді коли або рівняння межі області D, або підінтегр. Функц. Містить вираз x*x+y*y. Оскідьки у полярних координатах диї вираз має досить простий вигляд x*x+y*y=ро*ро*cos*cosфі+ ро*ро*sin*sinфі= ро*ро.

2)Яих треба обчислити подв. Інтегр. У порлярних координатах він функції F(ро,фі) по області G, яка обмежина промінями фі= альфа і фі= альфа , альфа<бета і лініями ро1=ро1(фі), то подвійний інтеграл по G = SSпо G f(x,y)dxdy=” ”(6)

3)Якщо область G містить точку О тобто т.О є внутрішньою точкою області G, а межа області G визн. Рівн. ро=ро(t), то под інтегр.

” ” (7)

4)Зазначимо, що при обмежині подвійн. Інтегр. У полярн. Коорд. Внутрішн. Інтегр. Завжд. Обчис. По що , а зовнішній по фі.