GeomCh

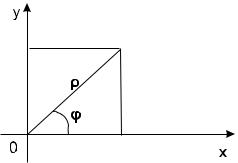
Замечание. При сложении векторов, их координанты складываются. При умножении вектора на число, его координаты умножаются на это число.

Определение. Декартова система координат это афинная система координат, такая что:

1.	Углы между базисными векторами прямые.
2.						e1	; e2 ; e3
	Длины векторов ¡! ¡! ¡! принимаются равными единице (т.е.
	j¡!j	=	j¡!j	=	j¡!j	= 1	).
	e1		e2		e3

3.Любую точку пространства можно отождествить с вектором, начало которого в точке 0, а конец в исходной точке.

Таким образом координаты любого вектора - суть в проекции его на соответствующие оси.

Полярная система координат:

0 · ½ < +1 , 0 · ' < 2¼ (рис.3)

Рис. 3:

10

Связь полярной и декартовой систем координат:

x = ½ cos(')	p
½ y½= ½ sin(')

½= x2 + y2

'= arctan(xy ) = arcsin(y½ ) = arccos(x½ )

Пример. B(¡1; 1) ) ½	½ = p
		2
	' = arctan(¡1) =			3¼
				4

Системы координат в пространстве Цилиндрическая система координат:

	x = ½ cos(')
8 y = ½ sin(')		(рис.4)
:	z = z0
<

					Рис. 4:
8
		½ =		x2 + y2
	'	y	arcsin(y ) = arccos(x )
		= arctan(x ) =p		½	½
:			z0 = z
<

Сферическая система координат:

r = jOAj, 0 · r < +1 , 0 · Á < 2¼.

11

	x = r cos(') cos(Á)
8 y = r sin(') cos(Á)		(рис.5)
:	z = r sin(Á)
<

Рис. 5:

>	p
			p				y
<	r =	x2 + y2					+ z2
							2 2
8	Ã = arcsin(						z			)
					x2+y2+z2
>
>				px +y
:	' = arcsin(							)
>

Определение. Осью называется прямая с выбранным направлением.

Определение. Проекцией вектора

AB

¡! на ось l называется длина от-

0

0

¡¡!0 0

¡¡!0 0

"# l) и

резка (A ; B

), взятая со знаком +(¡), если A B

"" l (A B

AB

обозначается Прl¡!.

(рис.6)

Свойства (проекции).

1. Прl

!¡

= j¡!j cos(¡!

).

a

a

a ; l

2. Прl

®!¡

=

Прl

¡!d.

a

®

a

¡!

3. Прl

(

!¡

+ ¡!)

a +

=Прl¡!

Прl

.

a

b

b

12

Рис. 6:

a ;

¡!

(

¡!) =

Определение. Скалярное произведение (¡!

b

) это число

a ; b

¡!

a

¡! =

!¡

cos(

¡!)

¡! ¢

j¡!j ¢ j

j ¢

\

b

b

¡!

a

a ; b

Свойства (скалярного произведения).

1. Алгебраические:

( a ;

¡!) = (¡!

)

(a)

¡!

b

b ; a

коммутативность.

a ; ¡!) =

¡!

(b)

(®

¢

¢

(

¡!

!¡ )

.

¡!

b

®

a ; b

)

(c)

( a + ¡!

) = (

) + (¡!

¡!

¡!

¡! ¡!

¡! .

(

b ;

c

a ; c

¡!

b ;

c

(d)

¡! ¡!

)

0

, если

¡!

=

6

.

a ; a

>

a

0

¡!

¡!

( a ;

¡!) =

a

=

a

Замечание. ¡!

b

j

b

b

.

j¢Прl¡!

j¡!j¢Прl

2.Геометрические:

(a)Скалярное произведение двух ненулевых векторов равно нулю , когда они перпендикулярны. То есть:

( a ; !¡ ) = 0			(		¡!) =
¡!		,		\		¼
				!¡		2
	b			a ; b

¡!

(b) Скалярное произведение вектора a на единичный вектор, сов-

!¡

падает с проекцией вектора a на ось единичного вектора.

13

(c)Скалярное произведение имеет знак + (-), когда угол между векторами острый (тупой).

3.Физический смысл: Работа, совершаемая силой по перемещению материальной точки по направлению вектора перемещения.

Лемма (Выражение скалярного произведения через декартовы коор-

a = (®

; ®

; ®

)

b

¯ ; ¯ ; ¯

)

,

¡! = (

1 2

3

,

тогда

динаты). Пусть векторы ¡!

1

2

3

b

® ¯

+

® ¯

+

® ¯ :

( a ; ¡!) =

1

1

2

2

3

3

¡!

a = ®1 e1

+ ®2 e2

+ ®3 e3

b

=

¯

e

1 +

¯ e

¯ e

(

a ; b

¡!

1

2 2 +

3 3

¡!

¡!) =

¤ !¡

!¡

¡!

¡!,

¡!

¡!

¡!,

(® e1

+®2 e2 +®3 e3

; ¯1 e1

+¯2 e2 +¯3 e3 ) =

по свойству 3

= (®1 e1 ; ¯1 e1 )+

1

¡!

!¡

¡!

¡!

¡!

¡!

j

!¡

¡!

(® e1

; ¯2 e2 ) + (®1 e1

; ¯3 e3 ) + (®2 e2

j

; ¯3 e3 ) +

; ¯1 e1 ) + (®2 e2

; ¯2 e2 ) + (®2 e2

1

¡!

¡!

¡!

!¡

¡!

¡!

¡!

¡!

¡!

¡!

(® e3

; ¯1 e1 ) + (®3 e3

; ¯2 e2 ) + (®3 e3 ; ¯3 e3 ) = ®1¯1(e1

; e1 ) + ®2¯2(e2

; e2 ) +

®

3

¡!

¡!

¡!

¡!

¡!

¡!

!¡

¡!

!¡

¡!

¯

(e3

; e3 ) = ®1¯1 + ®2¯2

+ ®3¯3

. ¥

3

3

!¡ ¡!

a

®2

®2

+

®2

j¡!j = q

1

+

2

3

\ ®1¯1 + ®2¯2 + ®3¯3
	b
cos( a ; ¡!) =
¡!		p®12 + ®22 + ®32p¯12 + ¯22 + ¯32

Определение. Базис называется ортогональным, если его вектора взаимоперпендикулярны.

Определение. Ортогональный базис называется ортонормированным, если длина всех его векторов равна единице.

Упражнение. j¡!j

=

j¡!j

=

j¡!j

= 1

,

¡! !¡ ¡!

. Вычислить

¡! ¡!

a1

a2

a3

a1 + a2 + a3

= 0

¡! ¡!

¡! !¡

(рис.7)

(a1; a2) + (a2; a3) + (a3

; a1)

¡!(

)

Пусть e1; e2; e3 базис.

a

x; y; z

cos(®) = p

x

x2 + y2 + z2

cos(¯) = p

y

x2 + y2 + z2

z cos(°) = px2 + y2 + z2 ;

¡!

где cos(®); cos(¯); cos(°) направляющие косинусы вектора a , cos2(®) + cos2(¯) + cos2(°) = 1:

14

Рис. 7:

Векторное произведение

Определение. Упорядоченная тройка некомпланарных векторов назы-

¡!

вается правой (левой), если из конца третьего вектора (a3) кратчайший поворот от первого вектора ко второму осуществляется против часовой стрелки (по часовой стрелке).

(рис.8)

			Рис. 8:
¡! ¡! !¡ правая.			¡! ¡! !¡ правая.	¡! ¡! !¡		правая.	¡! ¡! !¡
e1 ; e2	; e3		e3 ; e1 ; e2	e2 ; e3	; e1		e2 ; e1 ; e3
левая.	!¡ ¡! !¡	левая. ¡! ¡! ¡! левая.
	e3 ; e2 ; e1		e1 ; e3 ; e2

15

¡! ¡!

Определение. Векторным произведением a и b называется вектор

¡!

c удовлетворяющий следующим условиям:

¡! ¡! ¡! ¡!

1. c ? a ; c ? b

¡! ¡! !¡ ¡!\¡! 2. j c j = j a jj b j sin( a ; b )

¡! ¡! ¡!

3. a ; b ; c правая тройка.

¡! !¡ ¡! !¡ !¡

Обозначается c = [ a ; b ] = a £ b (рис.9)

Рис. 9:

Упражнение.

¡! ¡!

!¡

,

¡! ¡!

¡!¡

!¡ ¡!

¡!

¡! ¡!

]

¡! ¡!

¡¡!

[e1 ; e2

] = e3

[e2

; e1 ] =

e3

; [e2

; e3

] = e1

; [e3 ; e2

] =

!¡

¡!

¡!

:

[e1

; e3

e3

; [e3

; e1

] = e2

Алгебраические свойства

1.

[ a ; !¡ ] =

¡

[¡!

]

¡!

¡!

b

b ; a

2.

[® a ; !¡ ] = [¡!

!¡

]

¡!

b

® b ; a

] + [¡!

3.

[ a + !¡

¡!

] = [

]

¡!

¡! ¡!

¡!

b ;

c

a ; c

b ;

c

!¡

4.

a = 0

или

!¡ = 0

[

¡!

] = 0

Если ¡!

~

~

, то

~

b

a ; b

!¡

= ¡e1 ;

16

Геометрические свойства

¡! ¡! ¡! ¡! ¡! ¡! ¡! ¡! ¡! ¡! ¡!

1. a 6= 0 ; b 6= 0 , [ a ; b ] = 0 , a и b коллинеарны ( a jj b )

c

=

[ a ; ¡!]

=

¡! sin(

¡!) = 0

sin(

!¡ ) = 0

¤ j¡!j

j

!¡

j

j¡!jj

j

\

,

\

,

b

b

¡!

¡!

( a ;

!¡ ) = 0

a

a ; b

a ; b

¡!

\

¼

a ; b

¡!

b

± или

коллинеарны. ¥

± , ¡!

2.Геометрический смысл: Длина векторного произведения численно равна площади параллелограмма натянутого на эти векторы.

Физический смысл:

!¡

Пусть твердое тело закреплено в точке A и в точке B действует сила F .

!¡ ¡! ¡!

Момент силы равен векторному произведению [F ; AB] = M:

Выражение векторного произведения в декартовых координатах

a

(® ; ® ; ® );

!¡

(

¯

; ¯

; ¯

)

:

Пусть !¡ имеет координаты

b

имеет координаты

1

¯

2

¡

3

1

2

3

[!¡ ¡!] =

µ¯

¯2 ¯3

¯

¯1 ¯3

¯

; ¯

¯1 ¯2

¯¶

a ; b

¯

®2 ®3

¯

;

¯

®1

®3

¯

¯

®1

®2

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

b¯

¯

¯

a = ®1 e1 + ®2 e2 + ®3 e3 ; ¡! = ¯ e1

+ ¯2 e2 + ¯3 e3

¤ (рис.10) ¡!

¡!

!¡

¡!

1

!¡

¡!

!¡

[ a ;

¡!] =

=

® ¯

[

1

1 ] +

)

¡!

b

j по алгебраическим свойствам (2,3) j

e

; e

¡!

1

1

¡! ¡!

1

2

!¡

] + ®1

¡! !¡

] + ®2

¯1

¡! ¡!

¡! ¡!

¡! ¡!

®

¯

[e1

; e2

¯3[e1 ; e3

[e2

; e1

] + ®2¯2[e2

; e2

] + ®2¯3[e2

; e3 ] +

3

1

!¡ ¡!

!¡ ¡!

¡! ¡!

¡! !¡

¡

!¡

¡!

®

¯

[e3

; e1

] + ®3¯2[e3 ; e2 ] + ®3¯3[e3 ; e3

] = ®1¯2[e1 ; e2

]

¯

®2¯1[e1

; e2 ] +

2 3 !¡ ¡! ¡

!¡ ¡!

¡! !¡ ¡

¡! !¡

¯2 ¯3

¯

¡!

¡

¯

®2 ®3

¯

® ¯ [e2 ; e3 ]

®3¯2[e2 ; e3 ] + ®1¯3[e1 ; e3 ]

®3¯1[e1 ; e3 ] =

¯

¯

e1

¯

1

3

¯

¯

1

2

¯

¯

¡!

¡!

¡!

¯

¯ ¯ ¯

¯

¯

¯

®1 ®3

¯

¯

®1

®2

¯

¯

e1

e2

e3

¯

e2

+

e3

=

¯

®1

®2

®3

¯

:

¥

¯

¯

¯

¯

¡!

¯

¯

¯

¯

!¡

¯

¯

¯

¯

¯

¯

¯

¯

Упражнение. Найти S4ABC; если¯

A(1; 2; 3);¯B(0; 1; ¡2); C(1; 1; 1):

17

Рис. 10:

Смешанное произведение векторов

¡! !¡ ¡!

Определение. Смешанным произведением векторов a ; b ; c называ-

¡! ¡! ¡!

ется число равное ([ a ; b ]; c ):

Геометрические свойства:

j¡!jj¡!j

¡! ¡!

¢

!¡ ¡!

¢

§

¡!

¡!

¡! ¡!

b

; c

x ; c

x c

\

S

Пр x

c

S

h

) = (

) +

cos(

x ; c

) =

=

(

) =

1. ([ a ; !¡ ]

= §V; где S площадь параллелограмма, h высота параллеле-

V

a ;

¡!

c

пипеда, объем параллелепипеда. (+¡!

b ;

¡!,

a ;

!¡

¡!)(рис.11)

- ¡!

b ;

c

2. Смешанное произведение равно нулю , векторы компланарны.

3. Смешанное произведение > 0 (< 0), если тройка правая (левая).

Алгебраические свойства:

¡!

!¡ ) =

([ a ;

!¡ ]

; c

) =

(

) = (

1. ¡!

b

jпо определениюj

a ; b ; c

c ; a ; b

¡!

¡!

) =

¡!

!¡

¡!

(¡!

) = (¡!

¡! ¡!

) = (

¡!

¡!

¡!

¡

(

!¡ ¡!

!¡ )

!¡ ¡!

¡

¡

b ; c ; a

b ; a ; c

c ; b ; a

a ; c ; b :

18

Рис. 11:

Выражение смешанного произведения через декартовы координаты:

a = (a1

; a2

b

b

; b ; b

; c

= (

c

1

; c

2

; c

;

a ; b

; c

) =

; a3); ¡!

= (¡!1

¡!2

¡!3 )

¡!

3 ) ([

¡!

¡!]

¡!

¯

¡! ¡! ¡!

¯:

¡! ¡! ¡!

¡!

a1

a2

a3

=

¡!

¡!

¡!

¡!b1

¡!b2

¡!b3

¯

¯

¯

c1

c2

c3

¯

¡!

¡!

¡!

¯

¯

¯

¯

¯

¯

a2

a3

a1

a3

a1

a2

b

¡!

!¡

;

¡!

¡!

;

¡!

!¡

[ a ; ¡!] =

¡!

µ¯

b

b

¯

¡

¯

b

b

¯ ¯

b

b

¯¶

¡!2

!¡3

¡!1

¡!3

¡!1

!¡2

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

¯

берем по модулю определитель,¯

он¯

равен¯

объему¯ ¯параллелепипеда.¯

3Уравнение прямой и плоскости

Различные уравнения прямой на плоскости

Общее уравнение прямой

(рис.12)

Любая прямая на плоскости задается уравнением ax + by + c = 0; a2 +

2

n

l; M

l:

Возьмем на прямой

l

произвольную точку

M x; y

;

b = 0:

0

¡!

?

2

( )

6

(¡¡¡!

¡¡¡!

тогда

¡¡¡!

?

¡! )

¡!

) = 0

= (

¡

0

¡

0

)

+

¡

0

M

0

0

M

x

; y

y

: ax by

M

n

M

M; n

: M

x

ax0 ¡ by0 = 0: ax + by + c = 0; где c = ¡ax0 ¡ by0:

19