groups_lections (Множества и группы)

первому условию подмножеству H принадлежит композиция элементов h * h –1, которая равна нейтральному элементу ε группы G. Значит и аксиома 2* выполняется на подмножестве H G при выполнении двух достаточных условий.

§ 2. ЦИКЛИЧЕСКИЕ ПОДГРУППЫ И ГРУППЫ.

Вместе с любым элементом a группы G этой группе принадлежит (по определению 1.1 бинарной алгебраической

операции) композиция a * a независимо от того, какому элементу группы она равна. Но из a G и a * a G следует, что и

композиция a* a* a принадлежит группе G. Таким образом можно утверждать, что композиция

a a a ,

( 2. 1 )

n

получаемая повторением элемента a группы любое число n раз, принадлежит той же группе. Если групповая операция является умножением, то композицию (2.1), записанную в виде

a a a = a n ,

( 2. 2 )

n

уместно назвать n – ой степенью элемента a. Если же групповая операция является сложением, то композицию (2.1), записанную в виде

a a a = na ,

( 2. 3 )

n

следует назвать n – кратным элемента a. Так как в дальнейшем мы будем заниматься преимущественно рассмотрением преобразований симметрии геометрических фигур, а композиция таких преобразований понимается как операция умножения, то надо будет пользоваться символами (2.2) и терминами, свойственными мультипликативным группам. К тому же такая символика и терминология удобней для рассмотрения циклических подгрупп и групп. Если же потребуется пе-

рейти к обозначениям (2.3) и терминам, свойственным аддитивным группам, то сделать это не составит труда.

Из равенства (2.2) вытекают правила сложения и умножения показателей степени элемента группы:

a na k = (a a a) (a a a) = (a a a)
n	k	n k

где n и k — натуральные числа,

( a n )k = (a a a) (a a a) (a a a)
n	n	n

= a n+k, ( 2. 4 )

= a n k. ( 2. 5 )

k

Вместе с любым элементом a обратный ему элемент a–1 тоже принадлежит группе G. Для элемента a–1 равенство (2.2) примет вид

a 1 a 1 a 1 = ( a 1)n .

( 2. 6 )

n

Интересно то, что элемент ( a 1)n является обратным для a n:

(a a a a)(a 1 a 1 a 1) = … = a a–1 = ε .

Здесь горизонтальными фигурными скобками обозначено, как сначала исчезает во взаимной нейтрализации (превращении в нейтральный элемент ε) первая пара соприкасающихся граничных элементов {a)(a –1} = ε из выражений в круглых скобках (по образцу формул (1.23 ), (1.24)), затем то же происходит со второй парой и т.д. вплоть до нейтрализации первого элемента из левой скобки последним элементом из правой скобки. Тем самым доказано, что

( a 1 )n = ( a n ) 1 = a– n ,

( 2. 7 )

и это позволяет отбросить скобки при записи равнозначных по содержанию символов ( a 1 )n и ( a n ) 1 , а на символ a – n смот-

реть как на отрицательную целую степень элемента a.

С помощью равенств (2.7) правила (2.4), (2.5) операций над натуральными (целыми положительными) степенями

41форумстудентов.рф42

Теорема 2.3.

элемента группы распространяются на любые целые отрица-

тельные степени:

a

– n

a

– k (2.7)

( a

1

)

n

( a

1

)

k

(2.4)

( a

1

)

n k

(2.7)

a

– (n+k)

= a

– n – k

,

( a n ) k

(2.7)

( a n ) 1

k

(2.7)

( a n )k

= a n k = a (–n)(– k).

В частности, если k = –n, то

a

n

a

– n

(2.7)

a

n

( a

n

)

1

= ε = a

n – n

= a

0

,

( 2. 8 )

т.е. нулевая степень любого элемента группы есть нейтральный элемент. Таким образом, соотношения (2.4), (2.5) распространяются на любые целые (положительные, отрицательные и нулевое) значения показателя степени:

a la r = a l+r,	l, r Z ,	( 2. 9 )
( al )r = a l r,	l, r Z .	( 2. 10 )

Замечателен тот факт, что множество всех степеней любого элемента a группы G образует подгруппу группы G. Мы докажем это, пользуясь мультипликативной формой записи, но не составит труда провести аналогичные рассуждения и

для произвольных композиций (2.1) a* a* …* a элемента a.

Теорема 2. 2. Подмножество {am } всех целых степеней любого элемента a группы G образует подгруппу в группе G.

Это легко доказывается с помощью двух достаточных признаков подгруппы (см. теорему 2.1).

1)Любые два элемента a l и a r принадлежат подмножеству {a m }, поскольку l и r целые числа. Но и произведение этих элементов a la r = a l + r принадлежит подмножеству {a m }, так как показатель степени l+r тоже целое число.

2)Элемент a r с любым целым показателем степени r принадлежит подмножеству {am}. Значит и обратный элемент a – r принадлежит подмножеству {am }, так как показатель степени (–r) тоже целое число.

Определение 2.2. Подгруппа {am } всех целых степеней любого элемента a группы G называется цик-

лической подгруппой группы G, а элемент a называется образующим элементом циклической подгруппы {am}.

Ясно, что в конечной группе G всякая её подгруппа, в том числе циклическая, будет конечной. Но как согласовать это с тем бросающимся в глаза обстоятельством, что при изменении целого показателя степени m от – до + вроде бы должно получиться формально бесконечное множество различных степеней am элемента a? Сейчасэто разъяснит

В группе Gn конечного порядка n всякая циклическая подгруппа {am } содержит лишь конечное число элементов, не превосходящее порядкагруппыGn .

Выход из кажущегося противоречия между конечностью группы Gn и формальной бесконечностью подмножества {am } заключается в том, что отнюдь не все степени a m в подмножестве {a m } представляют действительно различные элементы группы Gn . Тогда надо признать, что найдутся такие

различные числа p и q, для которых
a p = a q .	( 2. 11 )

Положим дляопределённости, что p < q, и введём обозначение q – p = r > 0, откуда следует q = p + r .

Тогда равенство (2.11) можно записать в виде a p = a p+r = a p a r ,

показывающем, что a r= ε есть нейтральный элемент. Следовательно, при любом выборе целого числа s будет справедливо равенство

ars = ( a r ) s = εs = ε ,

доказывающее, что в циклической подгруппе {a m } нейтральный элемент ε = a 0 группы Gn встречается бесконечно много раз. Иэто характерно не только для нейтрального элемента, но и для любой степени образующего элемента подгруппы {am}.

Пусть k > 0 — наименьшее положительное целое чи-

сло, удовлетворяющее условию
a k = ε,	k > 0 ,	k — наименьшее.	( 2. 12 )

Тогда в множестве элементов

43форумстудентов.рф44

a0 = ε, a , a2, a3, … , a k–1

( 2. 13 )

все k элементов различны. Докажем это от противного. Допустим, что найдутся такие натуральные числа i и j, удовлетворяющие условиям

0 i < j k – 1 ,	( 2. 14 )
для которых может выполняться равенство
a i = a j .	( 2. 15 )

Введя обозначение j – i = t > 0, запишем j = i + t и представим

(2.15) в виде

a i = a i+t = a i a t ,

показывающем, что a t = ε есть нейтральный элемент. Но последнее равенство невозможно, так как из (2.14) следует

0 < t = j – i < j k – 1 < k ,

что противоречит исходному условию (2.12), согласно кото-

рому k есть наименьшее положительное целое число, при котором a k = ε, и потому при t < k не может быть a t = ε.

Легко убедиться в том, что при значениях показателя степени m, выходящих за пределы диапазона (2.14), т.е. при

m < 0 и m > k – 1 ,

каждый элемент из множества (2.13) будет циклически по-

вторяться (с периодом k):

a–1 = εa–1 = a ka–1 = a k–1,

a–2 = εa–2 = a ka–2 = a k–2,

. . . . . . . . . . . . . . . . . . . . . .

a– k = εa– k = a ka– k = a k– k = a0 = ε,

a k = a0 = ε,

a k+1 = a ka = εa = a ,

a k+2 = a ka2 = εa2 = a2 ,

. . . . . . . . . . . . . . . . . . . .

a k+k = akak = εak = ak .

Определение 2.3. Порядком конечной цик-

лической подгруппы {a m } называется наибольшее число различных элементов в ней.

Определение 2.4. Порядком элемента груп-

пы называется порядок конечной циклической подгруппы, образованной этим элементом.

Замечание 1. Необходимым добавлением к определениям 2.3 и 2.4 служит тот доказанный выше факт, что порядок конечной циклической подгруппы {a m } и порядок образующего элемента a этой подгруппы численно равен тому

наименьшему положительному целому показателю k, при котором a k = ε.

Замечание 2. Нейтральный элемент является един-

ственным элементом первого порядка, ибо никакой другой элемент, кроме нейтрального, не может образовать группу (а значит и подгруппу — см. определение 2.1) первого порядка.

Так как всякая подгруппа является группой (по определение 2.1), то циклические подгруппы являются цикличе-

скими группами.

Определение 2.5. Группа G называется цик-

лической, если она состоит только из степеней одного из своих элементов, т.е. совпадает с одной из своих циклических подгрупп.

Вполне очевидно, что всякая конечная циклическая группа Gn (порядка n) изоморфна группе вращений прави-

льного n –угольника.

Теорема 2.4. Всякая бесконечная циклическая

группа изоморфна аддитивной группе целых чисел, в которой роль образующего элемента играет число 1 или (–1).

При доказательстве теоремы 2.3 мы видели, что из совпадения хотя бы двух степеней элемента группы с различными значениями показателя степени (см. (2.11): a p = aq, p ≠ q) логически вытекает конечность циклической подгруппы. Поэтому в бесконечной циклической подгруппе (группе) не может выполняться равенство a p = a q при p ≠ q, т.е. из различия любых целых чисел p и q должно следовать различие элементов a p ≠aq. Но это означает (см. определение 0.4 в §1 вводной главы), что существует взаимно однозначное отображение

45форумстудентов.рф46

(биекция) бесконечной циклической группы {am} на аддитив-

ную группу Z целых чисел

f ({am}) = Z , ( 2. 16 )

при котором каждой степени a p элемента a соответствует целое число p:

f (a p ) = p .

( 2. 17 )

Во взаимной однозначности отображения (2.16) заключено выполнение двух первых требований (см. перечень их после формулы (1.31) в § 6 гл. 1) определения 1.8 изоморфизмов. Поэтому остаётся доказать только выполнение требования (1.31)

f (a) * f (b) = f (a * b) ,

называемого сохранением операции при изоморфном отображении. В тексте перед определением 1.8 было сказано, что сохранение операции не следует понимать буквально и может оказаться, что операции умножения элементов в группе– прообразе соответствует операция сложения элементов группы – образа. Теперь именно с таким случаем мы и встретились, что заставляет перейти к обобщённому обозначению групповой

операции звёздочкой (*) в начале и конце цепочки промежуточных преобразований, но пользоваться конкретными символами умножения и сложения внутри этой цепочки:

f (a p * aq ) = f (a paq ) = f (a p+q ) (2.17) p+q (2.17)	f (a p ) + f (a q ) =
= f (a p) * f (aq) .	( 2. 18 )

Здесь элементы a p иaq бесконечной циклической группы {am} отображаются на целые числа p и q — элементы аддитивной циклической группы Z с образующим элементом 1 или (–1).

Замечание 3. Теперь надо подчеркнуть, что любые группы 2-го и 3-его порядка по необходимости являются циклическими. На основании общих свойств таблиц Кэли в начале § 7 гл. 1 были построены однозначно таблицы (1.36), (1.37) абстрактных групп G2 и G3 . Как видно из таблицы (1.36), aa = a2 = ε, и это означает, что оба элемента группы G2 являются степенями образующего элемента a (см. также оп-

ределение 2.5), который имеет порядок 2. Таблица же (1.37) показывает, что aa = a2 = b, ab = aa2 = a3 = ε, т.е. все элементы

группы G3 являются степенями элемента a, имеющего порядок 3. Равным образом, элемент b, отличный от a и от нейтрального элемента, имеет порядок 3: bb = b2 = a, ba = bb2 = b3 = = ε, и каждый из отличных от нейтраль-

ного элементов группы G3 может слу-	G3	ε	a	a2
житьобразующим элементом этой цик-	ε	ε	a	a2
лической группы. Поэтому при записи	a	a	a2	ε
элементов группы G3 и её таблицы Кэ-	a2	a2	ε	a

ли следует отражать циклический характер группы, пользуясь обозначениями лишь одного из обра-

зующих элементов: G3 = {a, a2, a3 = ε} и делая исключение для нейтрального элемента с его специфическим символом ε.

Замечание 4. В конце § 7 гл. 1 было выяснено, что возможны только два типа существенно различных абстрактных групп четвёртого порядка, с

одним из которых совпадёт (с		G4(2)	ε	a		a2	a3
точностью	до изоморфизмов)	ε	ε	a		a2	a3
любая конкретная группа четвё-
		a	a	a2		a3	ε
ртого порядка. Теперь необходи-
		a2	a2	a3		ε	a
мо отметить, что абстрактная
		a3	a3	ε		a	a2
группа G4(2)	является цикличес-
			( 2. 19 )
кой и её таблицу Кэли следует

записывать в виде (2.19).

§ 3. НОРМАЛИЗАТОР ЭЛЕМЕНТА ГРУППЫ.

Подчеркнём, что любая циклическая группа является коммутативной, или абелевой (см. конец §2 вводной главы), потому что любые степени одного и того же элемента группы коммутируют (перестановочны): a pa q = a qa p = a p + q. Но даже в некоммутативной группе (где не для любых элементов a и b

возможно равенство a * b = b * a) есть подмножества коммути-

47форумстудентов.рф48

рующих между собой элементов. Во всяком случае в силу общихсвойств (1.3), (1.17), (1.4), (1.15) справедливы равенства

a* = * a = a , a* a –1 = a –1* a = .

Но сверх этих общих соотношений могут существовать в некоммутативных группах и более широкие подмножества коммутирующих между собой элементов.

Оп ределение 2.6. Подмножество N(a) всех тех элементов группы G, которые коммутируют (перестановочны) с элементом a G называется нормализатором элемента a.

Теорема 2.5. Нормализатор N(a) элемента a G является подгруппой группы G.

Это доказывается с помощью двух достаточных признаков подгруппы (теоремы 2.1 из §1 гл.2).

1) Если элементы b, c G коммутируют с элементом a G

a* b = b* a, a* с= с* a, ( 2. 20 )

то это значит, что они принадлежат подмножеству N (a) G. Но тогда и композиция этих элементов b* с коммутируетс элементом a, и следовательно принадлежит подмножеству N(a):

a * (b* c) 1 (a* b) * c (2.20) (b* a) * c 1 b * (a* с) (2.20)
(2.20)	b * (с* a) 1 (b* с) * a .
2) Если элемент b принадлежит N(a), то это значит, что
	a* b = b* a,
откуда следует	a = b –1* (a* b),
а из последнего равенства вытекает по аксиоме 1* группы
a = (b –1* a)* b
	(b –1* a) = (a* b –1) ,
т.е. перестановочность обратного к b элемента b –1 с элемен-
том a. Следовательно,	вместе с b и b–1 принадлежит подмно-
жеству N(a).

Задание № 3. Построить таблицу Кэли группы преобразований симметрии треугольного диэдра.

Задание № 4. В группе преобразований симметрии треугольного диэдра указать порядки всех её элементов. Найти все циклические подгруппы этой группы и нормализаторы всех элементов группы треугольного диэдра.

§ 4. РАЗЛОЖЕНИЕ ГРУППЫ ПО ПОДГРУППЕ НА ПРАВЫЕ СМЕЖНЫЕ КЛАССЫ.

К этому важнейшему понятию теории групп мы подойдём от наглядного простого примера. Убедимся в том, что все шесть подстановок множества, состоящего из трёх элементов А, В, С (см. ( 0. 9 ) в конце §1 вводной главы)

ABC

ABC

ABC

ABC

ABC

,

AC B ,

C B A ,

B A C

G6(1)

ε

a

b

c

d

d2

ε

ε

a

b

c

d

d2

a

a

ε

d

d2

b

c

b

b

d2

ε

d

c

a

c

c

d

d2

ε

a

b

d

d

c

a

b

d2

ε

d2

d2

b

c

a

ε

d

( 2. 22 )

,

ABC	,	ABC	, ( 2. 21 )
B C A		C AB

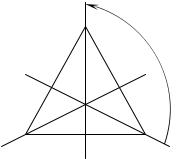
образуют группу 6-го порядка с таблицей Кэли (2.22). Отождествляя элементы A, B, C с вершинами правильного треугольника, нетрудно будет увидеть, что первая подс-

ABC

тановка = ε есть

ABC

не что иное как тожественное преобразование треугольника,

ABC

подстановка = a, оставляющая неизменной вершину A

AC B

и меняющая местами вершины B и C, соответствует операции отражения треугольника относительно биссектрисы AO при изоморфном отображении группы подстановок (2.21) множества трёх элементов на группу преобразований симметрии правильного треугольника. Аналогично очевиден смысл операций отражения относительно биссектрис b и c:

49форумстудентов.рф50

ABC	ABC			ABC
C B A = b,	BAC	= c. Операция B C A = d изоморфна
повороту правильного треугольника вокруг его центра O на
o		ABC	2	представляет двойной ми-
угол 120 , а операция		C AB = d

нимальный поворот на угол 240o в том же направлении. Элементы a, b, c имеют порядок 2 и образуют цикличе-

ские подгруппы второго порядка
H2(a) = {ε, a},	H2(b) = {ε, b},	H2(c) = {ε, c},	( 2. 23 )
а элемент d порядка 3 образует циклическую подгруппу
	H3 = {ε, d, d2}.		( 2. 24 )

Будем умножать подгруппу H2(a) (каждый её элемент) последовательно на различные элементы группы G6(1) и по таблице (2.22) вычислять множества получающихся произведений:

H2(a) = = (ε, a);			H2(a)a = a a				= (ε, a);
	a a			aa
H2(a) b = b b		= (b, d );	H2(a)c = c c				= (c, d2 );
	ab d			ac d 2
d d		= (b, d );	H2(a)d 2	d 2	d 2			2 ).
H2(a)d =				=	c		= (c, d
ad b				ad 2

					Как видим, произведение под-
	B				группы H2(a) на каждый из элемен-
				d	тов группы G6(1) представляет под-
					множество, состоящее из двух эле-
	a	c			ментов. Каждое такое подмножес-
	O				тво называется смежным клас-
					сом группы G6(1) по подгруппе
C	b		A		H2(a) , а точнее — правым смеж-
					ным классом (в знак того, что
	Рис. 1.2				тот элемент группы, на который
					умножается подгруппа, выступает

в роли правого сомножителя. Понятно, почему общее число правых смежных классов равно 6 (числу элементов группы G6(1) ). Интересно и весьма важно то обстоятельство, что среди

смежных классов есть одинаковые, а различных (не пересекающихся) правых смежных классов только 3:

(ε, a),

(b, d ),

(c, d2 ).

( 2. 25 )

Аналогичным способом найдём все правые смежные классы группы G6(1) по подгруппе H3 (2.24):

H3 ε = d d	= (ε, d, d2 );
d 2 d 2
b b
H3 b = db a = (a, b, c);
d 2b c
d d
H3 d = d d d 2	= (ε, d, d2 );
d 2d

	a a
H3 a = d a c = (a, b, c);
	d 2a b
	c c
H3 c = dc b = (a, b, c);
	d 2c a
	d 2	d 2
H3 d2				= (ε, d, d2 ).
	= d d 2
		2 d
	d 2d

Среди этих шести смежных классов только два различных (не пересекающихся):

(ε, d, d2 ), (a, b, c). ( 2. 26 )

Обратим внимание на то, что произведение порядка подгруппы на числонепересекающихся смежных классов по этой подгруппе равно порядку группы, разлагаемой на смежные классы по данной подгруппе, причём все элементы группы оказываются распределёнными между непересекающимися смежными классами так, что каждый элемент попадает только в один из непересекающихся смежных классов. Это является общей закономерностью, о которой речь впереди. Интересно и то обстоятельство, что умножая подгруппу на любой содержащийся в ней элемент, можно получить только эту же подгруппу, что естественно, так как всякая подгруппа является

51форумстудентов.рф52

группой, а произведение (композиция) любых элементов группы принадлежит этой группе (согласно определению 1.2 группы и определению 1.1 алгебраической операции). Таким образом, один из непересекающихся смежных классов по подгруппе необходимо совпадает с этой подгруппой.

Теперь можно перейти к общему доказательству свойств разложения любой абстрактной группы G на правые смежные классы по подгруппе H. Ради удобства изберём мультипликативную форму записи композиций, что не нарушит общей истинности получаемых результатов.

Общие свойства правых смежных классов.

1♦. Если a H, то Ha = H

( 2. 27 )

— подгруппа H сама является одним из смежных классов по подгруппе H. Так как подгруппа H является группой, то она содержит в себе композиции (произведения) любых своих элементов, т.е. из h H и a H следует ha H. И так как ha может служить представителем любого элемента смежного класса Ha, то запись ha H означает, что весь смежный класс Ha включён в подгруппу H: Ha H. Но подгруппе H принадлежит вместе с элементом a обратный элемент a –1, и композиция (произведение) ha –1 принадлежит H при любом выборе элемента h H. Значит ha –1 может служить представителем любого элемента подгруппы H, а произведение (ha–1 ) a является элементом смежного класса Ha. Таким образом, запись

(ha–1)a Ha обретает тот общий смысл, что H Ha, поскольку (ha–1)a = h (a–1 a) = hε = h H. Совместное выполнение со-

отношений Ha H и H Ha означает, что Ha = H.

2♦. В смежном классе Hb содержится элемент b.

В общем случае в смежном классе Hb содержится элемент hb, если h H, но в общем случае hb ≠ b. Однако в подгруппе H есть нейтральный элемент ε, и для него справедливы соотношения εb H, εb = b, b Hb. Это простое свойство имеет важ-

ный смысл: каждый элемент b группыG попадает по край-

ней мере в один из смежных классов по подгруппе H — в класс Hb.

3♦. Если ab–1 H, то Ha = Hb.

( 2. 28 )

Доказательству этогосвойства нужно предпослатьследующее

Замечание. Из ассоциативности композиций (произведений) любых элементов группы (по аксиоме 1*) вытекает

ассоциативность произведения любых подмножеств груп-

пы. Действительно, операция перемножения подмножеств группы заключается в том, что каждый элемент одного подмножества умножается на каждый элемент другого подмножества. Именно так выполняется умножение подгруппы на любой элемент группы (рассматриваемый в качестве частного случая подмножества) при построении смежных классов. Передвигание скобок в произведении (композиции) трёх и более подмножеств группы сводится к передвиганию скобок в произведениях элементов подмножеств, что оправдано аксиомой ассоциативности 1* группы. Ассоциативностью произведений подгрупп и смежных классов по подгруппе мы будем пользоваться в дальнейшем, и воспользуемся сейчас в конце цепочки равенств, доказывающей свойство 3♦ правых смежных классов:

Ha 2 H(aε) 1+	H{a(b–1b)} 1 H{(ab–1 )b)}	1
1	{H(ab–1 )}b 3 ,1 Hb.	( 2. 29 )

Последнее равенство в цепочке (2.29) основано на том, что элемент ab –1 по условию 3♦ (2.28) принадлежит подгруппе H, а отсюда следует по свойству 1♦ (2.27), что H(ab–1 ) = H.

4♦. Если смежные классы Ha и Hb имеют общий

элемент, то они совпадают: Ha = Hb.

Другая формулировка: два правых смежных класса

группы G по подгруппе H либо совпадают, либо не пересе-

каются (не имеют общих элементов).

53форумстудентов.рф54

Пусть какой-нибудь элемент hia Ha совпадает с неко-

торым элементом hkb Hb, где hi, hk H:
	hia = hkb .		( 2. 30 )
Найдём отсюда a: a = hi	1 (hkb) = ( hi	1 hk) b. Поэтому
ab–1={( hi 1 hk) b}b–1 1 ( hi 1 hk)(bb–1) 3 ( hi 1 hk) ε 2			hi 1 hk H.

Из доказанной здесь принадлежности элемента ab –1 подгруппе H следует по свойству 3♦ (2.28) смежных классов: Ha = Hb.

Свойство 4♦ особенно важно, так как позволяет однозначно указать смежный класс, указав хотя бы один из принадлежащих ему элементов. Действительно, если g Ha, то элемент g не может принадлежать какому-нибудь правому смежному классу, отличному от Ha. Иначе говоря, все элементы

группы G распределены между не пересекающимися правыми смежными классами по подгруппе H. Это распределение называют правосторонним разложением группы G по подгруппе H. Отсюда происходит обычай называть подгруппу делителем группы в знак того, что с помощью подгруппы можно разделить группу на непересекающиеся смежные классы.

§ 5. ТЕОРЕМА ЛАГРАНЖА И СЛЕДСТВИЯ ИЗ НЕЁ.

Теорема 2.6. В конечной группе Gn порядка n порядок k любой подгруппы Hk является делителем порядка

группы

n	i N	( 2. 31 )
k

(здесь подчёркнуто, что частное i принадлежит множеству N натуральных (целых положительных) чисел, как и порядки n, k группы и подгруппы). Доказательство теоремы 2.6 основано

на свойстве 4♦ смежных классов. Все смежные классы группы Gn по подгруппе Hk содержат одинаковое число элементов, равное порядку k подгруппы. Так как каждый элемент g группы

Gn порождает смежный класс Hk g, то получаются n смежных классов. Однако, как видно из примеров (2.25), (2.26), среди этих n смежных классов могут оказаться одинаковые (хотя это не всегда обязательно), и тогда число действительно различных (не пересекающихся) смежных классов будет меньше. Во всяком случае, число i n не пересекающихся смежных классов по подгруппе Hk будет натуральным, и по этим i классам, каждый из которых содержит k элементов, распределятся все n элементов группы Gn , что позволяет написать равенство

i k = n ,

( 2. 31 )

равносильное доказываемому равенству (2.31).

Число i непересекающихся смежных классов по подгруппе Hk является важной характеристикой этой подгруппы и называется индексом подгруппы Hk .

Замечание. Утверждение, обратное теореме Лагранжа, может и не быть справедливым, т.е. из того, что некоторое число l является делителем порядка группы Gn , не следует с необходимостью существование подгруппы порядка l в группе Gn .

Следствие 1 из теоремы Лагранжа. Порядок

любого элемента конечной группы является делителем порядка группы.

По определению 2.4 (в § 2 гл. 2) порядком элемента группы называется порядок циклической подгруппы, образованной этим элементом, и это число является делителем порядка группы согласно теореме Лагранжа.

Следствие 2 из теоремы Лагранжа. Всякая группа, порядок которой простое число, является цикличес-

кой.

Если n — простое число, то в группе могут быть только элементы порядка 1 и порядка n. Элемент порядка 1 — это

55форумстудентов.рф56

нейтральный элемент, присутствующий в каждой группе (по аксиоме 2*). Если n > 1, то в группе Gn есть хотя бы один элемент, отличный от нейтрального, и порядок каждого элемента, отличного от нейтрального, может быть равен только n согласно следствию 1. Образованная таким элементом циклическая подгруппа имеет n различных элементов (см. определение 2.3 в § 2 гл. 2) и совпадает с группой Gn (см. определение 2.5). При этом нейтральный элемент ε является n-ой степенью любого образующего элемента (см. замечание 1 в §2 гл. 2).

§6. НОРМАЛЬНАЯ ПОДГРУППА ( НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ).

Впоследнем абзаце § 4 гл. 2 объяснено, почему подгруппу называют иногда делителем группы. Но, стремясь к более однообразной терминологии, мы будем в дальнейшем говорить о нормальных подгруппах. Понятие нормальности подгруппы связано с рассмотрением левостороннего разложения группы по этой подгруппе. Если в произведениях подгруппы H на элементы группы G эти элементы выступают в роли левых сомножителей: aH, bH, …, то получаются левые смежные классы по подгруппе H. Рассмотрим конкретные примеры, как в начале § 4. Будем умножать каждый элемент

группы G (1)		(см. таблицу (2.22)) на подгруппу H				(a)		= {ε, a}:
	6					2
H2(a)	=			= (ε, a);	aH2(a) = a a	= (ε, a);
		a a			aa
bH2(a) = b b				= (b, d2 );	cH2(a) = c c		= (c, d );
	ba d 2				ca d
d H2(a) =	d d		= (с, d );		d 2 d		2	= (b, d2 ).
					d 2 H2(a) =
	da c				d 2a b

Здесь, как и в рассмотренном в начале § 4 примере с правыми смежными классами по подгруппе H2(a) , имеем 6 смежных

классов, среди которых только 3 различных (не пересекающихся). Но множество левых непересекающихся смежных классов

(ε, a), (b, d2 ), (c, d ) ( 2. 32 )

отличается от множества (2.25) правых непересекающихся смежных классов по той же подгруппе H2(a) . Именно потому,

что левостороннее разложение группы G6(1) по подгруппе H2(a)

не совпадает с правосторонним разложением по ней, эта подгруппа не заслуживает названия нормальной.

Найдём левые смежные классы группы G6(1) по под-

группе (2.24) H3 = {ε, d, d2}:

εH3 =		d d		= (ε, d, d2 );
	d 2 d 2
		b b
bH3 = bd c = (a, b, c);
		bd 2 a
	d d
dH3	= d d d 2		= (ε, d, d2 );
	d d 2

	a a
aH3 = ad b = (a, b, c);
	ad 2 c
	c c
cH3 = cd a = (a, b, c);
	cd 2 b
	d 2 d 2
d2H3			= (ε, d, d2 ).
	= d 2d
	d 2d 2 d

Два левых непересекающихся смежных класса группы G6(1)

по подгруппе H3	(a, b, c)	( 2. 33 )
(ε, d, d2 ),

совпадают с правыми непересекающимися смежными классами (2.26) по той же подгруппе. Иначе говоря, левосто-

роннее разложение группы G6(1) по подгруппе H3 совпадает с

правосторонним разложением. Благодаря этому свойству подгруппа H3 в составе группыG6(1) является нормальной.

Нормальные подгруппы играют важную роль в теории групп, и для лучшего усвоения этого понятия, нужно убедиться, что для левых смежных классов группы G по любой её

57форумстудентов.рф58

подгруппе H справедливы свойства, аналогичные свойствам 1♦, 2♦, 3♦, 4♦ правых смежных классов, доказанным в §4 гл. 2.

♦1. Если a H, то aH = H.	( 2. 34 )
♦2. В смежном классе bH содержится элемент b.
♦3. Если a–1b H, то aH = bH.	( 2. 35 )

♦4. Если смежные классы aH и bH имеют общий элемент, то они совпадают: aH = bH. ( 2. 36 )

Читателю рекомендуется самостоятельно доказать свойства ♦1, ♦2, ♦3, ♦4 левых смежных классов по образцу доказательств свойств правых смежных классов.

Определение 2.7. Подгруппа H группы G называется нормальной подгруппой (нормальным делителем группы G), если левостороннее разложение группы G по подгруппе H совпадает с правосторонним разложением G по H, т.е. каждый левый смежный класс aH совпадает с какимнибудь правым смежным классом Hb:

a G b G: aH = Hb . ( 2. 37 )

В этом определении не требуется, чтобы для каждого элемента a G выполнялось равенство a H = Ha в случае нормальности подгруппы H. Но мы докажем, что выполнение равенства a H = Ha для каждого элемента группы G является

необходимым и достаточным признаком нормальности

подгруппыH.

Теорема 2. 7 (первый необходимый и достаточный признак нормальности подгруппы). Для того что-

бы подгруппа H группы G была нормальной, т.е. чтобы выполнялось условие (2.37), необходимо и достаточно выпол-

нение для каждого элемента a G равенства
aH = Ha , a G .	( 2. 38 )

Необходимость. Исходим из того, что выполнено условие (2.37), означающее нормальность подгруппы H. Тогда

по свойству ♦2 левых смежных классов

aaH

ина основании равенства (2.37) можно утверждать, что

a Hb .	( 2. 39 )
А так как по свойству 2♦ правых смежных классов
a Ha ,	( 2. 39 )

то смежные классы Hb и Ha имеют общий для них элемент a и согласно свойству 4♦ правых смежных классов совпадают:

Hb = Ha .

Подставив последнее равенство в (2.37), получаем равенство (2.38) в качестве необходимого следствия условия нормальности (2.37) подгруппы H в группе G.

Достаточность. При доказательстве достаточности условия (2.38) исходим из того, что оно выполнено. Но оно представляет собой более жёсткое требование, чем требование (2.37), и в этом качестве является частным случаем условия (2.37). Значит при выполнении (2.38) оказывается выполненным и условие (2.37), являющееся признаком нормальности подгруппы H.

Замечание 1. В абелевой (коммутативной) группе G все подгруппы H нормальные, так как из условия коммутативности группы G

	ab = ba ,	a, b G
следует	aH = Ha ,	a G .

Замечание 2. Всякая подгруппа индекса 2 — нормальная. Это надо не забывать. Индекс i подгруппы H равен числу смежных классов (всё равно, правых или левых) по этой подгруппе (см. (2.31), (2.31 )). А так как сама подгруппа H совпадает с одним из непересекающихся смежных классов по ней (см. (2.27), (2.34)), то во второй смежный класс попадают все остальные элементы группы, не принадлежащие подгруппе H, и это распределение всех элементов группы по двум смежным классам не зависит от того, строим ли мы пра-

59форумстудентов.рф60