groups_lections (Множества и группы)

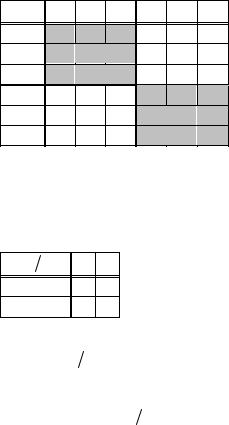
вые или левые смежные классы, как наглядно показывает сравнение (2.26) с (2.33).

§ 7. ФАКТОР – ГРУППА.

Самое замечательное свойство нормальных подгрупп заключается в том, что множество всех непересекающихся смежных классов группы G по нормальной подгруппе H образует группу, в общем случае отличную от группы G, и называемую фактор – группой группы G по подгруппе H — обозначение

G /H.

В предыдущих параграфах 4 и 6 мы рассматривали произведения подгруппы H на отдельные элементы группы G, что давало в результате смежные классы по подгруппе H. Теперь рассмотрим произведения, в которых роль обоих сомножителей будут играть смежные классы (2.33) группы G6(1) по

нормальной подгруппе (2.24) H3 = {ε, d, d 2}. Легко видеть, что умножая класс (ε, d, d2 ) на самого себя, получим в качестве произведения этот же смежный класс:

(ε, d, d2) (ε, d, d2) = (ε, d, d2) ,

потому что произведение любых элементов подгруппы (в данном случае подгруппы H3) может быть только элементом этой же подгруппы. Далее находим

a a

(ε, d, d2) (a, b, c) = d a c

d 2 a b

a a

(a, b, c) (ε, d, d2) = ad b

ad 2 c

aa

(a, b, c) (a, b, c) = ab d

ac d 2

b b	c c
db a	d c b = (a, b, c) ,
d 2b c	d 2c a
b b	c c
bd c	cd a = (a, b, c) ,
bd 2 a	cd 2 b
ba d 2	ca d
bb	cb d	2		= (ε, d, d	2	) .
bc d	cc

G6(1)		ε	d		d2	a		b	c	Полученные	результаты
ε		ε	d		d2	a		b	c	можно представить более
										наглядно, разместив над-
d		d	d2		ε	c		a	b
										лежащим образом элеме-
d2	d2		ε		d	b		c	a
										нты группы G6(1) из табли-
a		a	b		c	ε		d	d2	цы (2.22) в виде таблицы
b		b	c		a	d2		ε	d	(2.40). Введя обозначе-
c		c	a		b	d		d2	ε	ния смежных классов
			( 2. 40 )							(ε, d, d2) = E , (a, b, c) = A ,
представим таблицу(2.40) в виде таблицы (2.40 ) группы вто-
рого порядка. Содержание таблицы (2.40) в точности такое
же, как в (2.22), но форма расположения элементов и их про-
изведений иная; зато она наглядно показывает, какие классы
G (1)	H		E	A		мы перемножали и какой класс получали в
6		3				качестве произведения. В укрупнённых
E			E	A клетках таблицы (2.40), отмеченных серой
A			A	E		заливкой, находятся только элементы сме-
( 2. 40 )						жного класса (ε, d, d 2 ) = E, выступающего
						в роли			нейтрального элемента фактор–
группы G (1)			H
				3	, а в двух других укрупнённых клетках (без за-
		6
ливки) находятся только элементы смежного класса (a, b, c) =
A. Совершенно закономерно, в роли нейтрального элемента
фактор-группы G (1) H							3	по нормальной подгруппе H3 высту-
					6

пает сама эта подгруппа.

Прежде чем приступить к доказательству общих истин, убедимся на конкретном примере, что если подгруппа не является нормальной, то смежные классы по этой подгруппе не будут элементами группы уже по той причине, что произведение таких смежных классов может и не быть смежным классом по той же подгруппе. Выше было показано, что подгруппа H2(a) группы G6(1) не является нормальной, так как левосто-

роннее разложение (2.32) по H2(a) не совпадает с правосторон-

ним разложением (2.25). Найдём, например, произведение левых смежных классов из множества (2.32) по таблице (2.40):

61форумстудентов.рф62

(b, d2 ) (c, d ) = bñ d			bd ñ				= (ε, a, c, d ) .
	2	ñ a	d	2
d					d

Это произведение оказалось множеством четырёх элементов, и уже по этой причине не является смежным классом по подгруппе H2(a) , который должен состоять из двух элементов.

После знакомства с конкретным примером, поясняющим наглядно смысл нового понятия, можно с заинтересованностью обратиться к общим доказательствам того, что множество смежных классов любой группы G по её нормальной подгруппе H образует группу (фактор-группу G / H ). Для начала надо доказать, что на множестве смежных классов по нормальной подгруппе определена бинарная алгебраическая операция (см. определение 1.1 в §1 гл. 1). Первые два пункта определения 1.1 ( из перечня после формулы (1.1)) окажутся выполненными, если мы докажем, что произведение любых смежных классов по нормальной подгруппе является смежным классом по этой же подгруппе. Однозначность произведения вытекает из того, что имеются в виду только не пересекающиеся смежные классы и однозначно произведение любых элементов группы, а требование упорядоченности пары сомножителей не является необходимым, как сказано в конце

§1 гл.1.

Теорема 2.8. Если H — нормальная подгруппа

группы G, то для любых элементов a, b G произведение смежных классов (Ha) (Hb) является также смежным классом по подгруппе H.

Доказывается это одной строкой равенств:

(Ha)(Hb) 1 H(aH)b (2.38) H(Ha)b 1 (HH)(ab) 1 , 1 H(ab). ( 2. 41 )

Здесь ссылка на формулу (2.38) означает использование первого необходимого и достаточного признака нормальности

подгруппы. Ссылка на свойства 1♦ и ♦1 (см. (2.27) и (2.34)) на-

поминает о том, что при умножении (всё равно, справа или слева) подгруппы H на любой элемент этой же подгруппы можно получить только элемент подгруппы H, вследствие чего справедливо равенство

HH = H .

Символ H(ab) обозначает смежный класс по подгруппе H, образованный умножением этой подгруппы на элемент (ab) группы G, который определён однозначно выбором упорядоченной пары элементов a, b G согласно определению группы (а именно, по определению бинарной алгебраической операции на группе).

Остаётся доказать, что операция умножения смежных классов по нормальной подгруппе удовлетворяет всем трём аксиомам группы (см. определение 1.2 в §2 гл.1).

Те о р ема 2. 9. Множество смежных классов по нормальной подгруппе образует группу, элементами которой являются эти смежные классы.

Выполнение требования (1.2) аксиомы 1* ассоциативности для произведения смежных классов не нужно доказывать, потому что это вытекает из ассоциативности композиций любых элементов группы (см. также замечание после формулы (2.28) в конце §4 гл.2).

Роль нейтрального элемента в множестве смежных классов по нормальной подгруппе H играет сама эта подгруппа, которая является также одним из смежных классов (см. (2.27) и последующий текст). Действительно, для любого

элемента a G справедливы равенства:

(Ha)H 1 H(aH) (2.38) H(Ha)b 1 (HH)a 1 , 1 Ha. ( 2. 42 )

То, что в результате умножения смежного класса (Ha) на подгруппу (смежный класс) H получается смежный класс (Ha), означает, что данной ситуации подгруппа H играет роль нейтрального элемента в множестве смежных классов. Требование (1.3) аксиомы 2* выполнено.

63форумстудентов.рф64

В роли элемента (Ha) – 1, обратного смежному классу (Ha), выступает смежный класс H(a–1), ибо произведение смежных классов (Ha){H(a – 1)} равно нейтральному смежному классу H:

(Ha){H(a		–1	)}	1		H(aH) a			–1 (2.38)				H(Ha)a		–1	1
1	(HH)(aa				–1	)	1 , 1	H(aa		–1	)	3	Hε	2	H.	( 2. 43 )

Требование (1.4) аксиомы 3* выполнено.

Итак, в теоремах 2.8 и 2.9 содержится доказательство того, что все четыре требования 0*, 1*, 2*, 3* (см. конец § 2 гл. 1) определения группы выполнены для множества смежных классов любой группы по её нормальной подгруппе.

Определение 2.8. Группа, элементами которой являются смежные классы группы G по нормальной подгруппе H G называется фактор-группой и обозначается символом G /H.

Фактор-группы играют важную роль в теории представлений групп, с помощью которой исследуется строение микроструктур (кристаллов, молекул, атомов).

Замечание. Так как в конечной группе Gn порядка n число непересекающихся смежных классов по подгруппе Hk порядка k равно индексу i = n / k подгруппы Hk (см. теорему 2.6 в начале§5 гл. 2), то фактор-группа Gn /Hk имеет порядок i.

Задание № 5. В группе преобразований симметрии треугольного диэдра найти все нормальные подгруппы и построить таблицы Кэли типа (2.40) фактор-групп по этим нормальным подгруппам.

§ 8. ОТНОШЕНИЕ СОПРЯЖЁННОСТИ МЕЖДУ ЭЛЕМЕНТАМИ ГРУППЫ И ЕГО СВОЙСТВА.

В коммутативной (абелевой) группе G для любых её элементовa, g G выполняется равенство

g* a = a* g .

( 2. 44 )

Если же группа G не коммутативная, то соотношение (2.44) выполняется не для всех элементов группы, но в таких случаях возможна неполноценная замена (суррогат) равенства

(2.44), состоящая в том, что найдётся такой элемент g , кото-
рый в роли правого элемента композиции
	a g приводит к

такому же результату, как элемент g в роли левого участника

композиции g* a	g .	( 2. 45 )
g* a = a

Легко видеть, что условию (2.45) удовлетворяет элемент g ,
определяемый формулой	–1		( 2. 45 )
g = a	g	* g * a .
Связь (2.45), (2.45 ) элемента		с элементом g называют со-
пряжённостью и обозначают кратко значком			≈
g	≈ g.		( 2. 45 )

Определение 2.9. В группе G элемент g называется сопряжённым с элементом g ( g ≈ g), если в этой

группе найдётся такой элемент a G, с участием которого выполняется равенство

	= a	–1	( 2. 46 )
g		* g * a .

Элемент a в соотношении (2.46) можно назвать сопрягающим элементом. Существенно, чтобы сопрягающий элемент a принадлежал той же группе, что и сопряжённые элементы g, g . Не исключено, что в группе G могут найтись

различные элементы, сопрягающие g с g.

Равенство (2.46) можно истолковать также как трансформирование (переделывание, преобразование) элемента g в элемент g с помощью элемента a, и тогда элемент a назы-

вают трансформирующим элементом.

Будем пользоваться в дальнейшем мультипликативной формой записи:

65форумстудентов.рф66

	–1	g a .	( 2. 46 )
g = a

Из этого определяющего соотношения вытекают три основных свойства отношения сопряжённости.

(1) Рефлексивность: каждый элемент сопряжён сам с

собой	g ≈ g	ибо	ε–1g ε = g	( 2. 47 )
(нейтральный элемент ε всегда может быть сопрягающим).
(2) Симметричность: если f сопряжён с g ( f ≈ g), то g
сопряжён с f	( g ≈ f ), ибо
из	f = a–1g a	следует	g = a f a–1	( 2. 48 )

(в последнем равенстве сопрягающим элементом служит a–1 ).

(3) Транзитивность:
если f ≈ g и g ≈ h ,	то	f ≈ h .	( 2. 49 )
Действительно, из f = a–1g a и g = b–1h b		следует

f = a–1(b–1h b) a = (a–1 b–1 ) h (ba) = (ba)–1 h (ba)

(в последнем равенстве сопрягающим элементом служит (ba).

§ 9. РАЗБИЕНИЕ ГРУППЫ НА КЛАССЫ СОПРЯЖЁННЫХ ЭЛЕМЕНТОВ.

Для того чтобы оценить по достоинству мощь этой идеи и попутно лучше вникнуть в технику нахождения сопряжённых элементов группы, найдём сначала классы сопряжённых элементов “кустарным” способом, применяя к каждому элементу группы G6(2) (см. таблицу (2.40) или (2.22)) со-

пряжение последовательно всеми элементами группы. На таком подробном примере, гарантирующем, что ничего нами не упущено, хорошо видны общие черты разбиения группы на классы сопряжённых элементов. Во-первых, имеет место разбиение на не пересекающиеся классы, а классы, имеющие хотя бы один общий элемент, полностью совпадают. Благодаря этому каждый класс сопряжённых элементов определяется однозначно любым присутствующим в нём элементом:

{ }		{a}		{b}		{c}		{d }		{d 2}
1		1a a		1b b		1c c		1d d		1d 2 d 2
a 1 a		a 1aa a		a 1ba c		a 1ca b		a 1d a d 2		a 1d 2 a d
b 1 b		b 1ab c		b 1bb b		b 1cb a		b 1db d 2		b 1d 2b d
c 1 c		c 1ac b		c 1bc a		c 1cc c		c 1d c d 2		c 1d 2c d
d 1 d		d 1ad c		d 1bd a		d 1cd b		d 1d d d		d 1d 2 d d 2
d 2 d 2		d 2 ad 2 b		d 2bd 2 c		d 2cd 2 a		d 2 d d 2 d		d 2 d 2 d 2 d 2
( )		( a, b, c)		( a, b, c)		( a, b, c)		( d, d 2 )		( d, d 2 )

Если бы мы знали эту особенность заранее, то обнаружив сопряжённость элементов c и b c элементом a, имели бы право не вычислять третий и четвёртый столбцы, а перейти сразу к пятому столбцу. Выяснив же в пятом столбце, что элемент d сопряжён только сам с собой и с элементом d 2, можно было уже не заниматься вычислением шестого столбца, а заодно получить уверенность в том, что отказавшись от вычисления третьего, четвёртого и шестого столбцов, мы ничего не пропустили, поскольку все элементы группы G6(2) оказались рас-

пределёнными между тремя непересекающимися классами

(ε) , (a, b, c) , (d, d2 ) ( 2. 50 )

Во-вторых, важной общей чертой классов сопряжённых элементов является то, что нейтральный элемент ε сопряжён только сам с собой и больше ни с каким иным элементом группы не сопрягается. В-третьих, видно, что все сопряжённые между собой элементы (принадлежащие одному классу) имеют одинаковый порядок (элементы второго порядка находятся в классе (a, b, c), а в классе (d, d 2 ) находятся элементы третьего порядка).

Теорема 2. 10. Всякая группа разлагается на не пересекающиеся классы сопряжённых элементов.

Обозначим через S ( f ) множество всех тех элементов группы G, которые сопряжены с элементом f , а через S( g) — множество всех элементов, сопряжённых с элементом g. Тео-

67форумстудентов.рф68

( 2. 51 )

рема будет доказана, если мы докажем, что в случае пересечения множеств S ( f ) и S ( g ) по не пустому множеству (содержащему хотя бы один элемент группы G)

S( f ) ∩ S(g) = h G

эти множества совпадают

			S( f ) = S(g) .		( 2. 52 )
Из	h S( f )	следует	h ≈ f	и по свойству (2)		f ≈ h .
Из	h S(g)	следует	h ≈ g ,	что вместе с	f ≈ h	даёт
по свойству транзитивности (3)				f ≈ g , и по (2)	→ g ≈ f .
Из	f ≈ g, т.е.	f S(g), следует, что и все сопряжённые с f эле-
менты (а это весь класс S( f )) принадлежат S(g), т.е.
Из g ≈ f , т.е.			S( f ) S(g) .		( 2. 53 )
		g S ( f ),	следует,	что и все сопряжённые с g
элементы (а это весь класс S(g)) принадлежат S( f ), т.е.
			S(g) S( f ) .		( 2. 53 )

Доказав справедливость следствий (2.53) и (2.53 ) из условия (2.51), заключаем, что совместное выполнение соотношений (2.53) и(2.53 ) означает выполнение равенства (2.52).

Замечание 1 . В коммутативной (абелевой) группе

G каждый элемент сопряжён только сам с собой и больше ни с каким другим элементом не сопряжён. Действительно, из условия коммутативности группы G

ab = ba , a, b G

( 2. 54 )

следует, что сопрягая любой её элемент b любым её элементом a, можно получить только элемент b:

a	–1	b a = a	–1	(2.54)	a	–1	1	(a	–1	a)b = εb = b .
			(ba)			(ab)

Замечание 2 . Из особенности коммутативных групп, указанной в замечании 1, следует, что в конечной абелевой группе порядка n число классов сопряжённых элементов равно порядку n группы.

В некоммутативной конечной группе число классов сопряжённых элементов меньше порядка группы. Этот признак удобен для обнаружения некоммутативности группы.

Задание № 6. Выполнить разложение группы симметрии треугольного диэдра на классы сопряжённых элементов.

Теорема 2.11. Сопряжённые элементы группы имеют одинаковый порядок.

Вспомним, что согласно определению 2.4 и последующему замечанию 1 в конце §2 гл. 2 порядком элемента группы называется порядок конечной циклической подгруппы, образованной этим элементом, и этот порядок совпадает с тем наименьшим положительным целым показателем степени, при возведении в который образующего элемента циклической подгруппы получается нейтральный элемент.

Пусть элемент f сопряжён с элементом g, имеющим порядок k:

k > 0 — наименьшее целое, при котором gk = ε. ( 2. 55 )

Тогда с учётом соотношения f = a–1g a между сопряжёнными элементами, можем вычислить k-ую степень элемента f :

f k = (a 1g a)(a 1 g a) (a 1 g a) = a 1g k a = a 1 a = . ( 2. 56 )

k

Мы доказали, что f k = ε, но не доказали, что нет ещё меньше-

го положительного целого числа p
	0 < p < k ,	( 2. 57 )
такого, чтобы было	f p = ε.	( 2. 57 )

Поэтому, предположив выполнение условий (2.57), (2.57 ), получим из f = a–1g a выражение g = a f a–1 (см. (2.48)) и найдём

g p = (a f a 1)(a f a 1) (a f a 1) = a f pa 1 = a a 1 = .

p

Равенство g p = ε, которое мы получили при допущениях (2.57), (2.57 ), противоречит исходному условию (2.55) и потому ложно. Тем самым опровергаются допущения (2.57), (2.57 ) и доказано, что элемент f имеет тот же порядок k, что и сопряжённый с f элемент g.

69форумстудентов.рф70

Замечание 3. Обратной силы эта теорема не имеет,

т.е. из того, что некоторые элементы группы G имеют одина-

ковый порядок, не вытекает с необходимостью сопряжён-

ность этих элементов в группе G. Например, в группе вращений правильного тетраэдра повороты вокруг осей третьего порядка на минимальный угол 2π/ 3 сопряжены между собой, но не сопряжены с поворотами вокруг тех же осей на двойной минимальный угол. Это объясняется тем, что в данной группе вращений нет ни одного элемента, способного выполнить сопряжение поворота на 2π / 3 с двойным поворотом. Но в полной группе симметрии тетраэдра, включающей в себя, кроме поворотов, отражения в плоскостях симметрии и зеркальные повороты, такие сопрягающие элементы имеются, и потому в полной группе симметрии тетраэдра все преобразования поворота вокруг осей третьего порядка попадают в один и тот же класс сопряжённых элементов.

Очень важным дополнением к теореме 2.11 является

Теорема 2.12. Число элементов в каждом классе сопряжённых элементов конечной группы является делителем порядка группы.

Эта теорема доказывается с помощью понятия нормализатора элемента (см. определение 2.6 и теорему 2.5 в § 3 гл. 2). Пусть в группе Gn порядка n подгруппа N(a) является нормализатором элемента a Gn . Так как в общем случае нормализатор элемента может не быть нормальной подгруппой, то при рассмотрении смежных классов по такой подгруппе нужно указывать, имеются ли в виду правые или левые смежные классы. Положим для определённости, что дальнейшие рассуждения будут относиться к правым смежным классам группы Gn по подгруппе N(a). Также для определённости положим, что мы будем рассматривать конкретный смежный класс {N (a)} g, образованный элементом g Gn , который однако может быть выбран в группе Gn совершенно произволь-

но. По свойству 2♦ g {N(a)}g, а согласно свойству 4♦ и разъяснению, данному в последнем абзаце § 4, выбором того или иного элемента g определяется один и только один из непересекающихся правых смежных классов по подгруппе N(a).

Трансформируя выбранным элементом g тот элемент a, которым определена подгруппа (нормализатор) N(a), полу-

чим некоторый элемент b Gn :
g–1a g = b.	( 2. 58 )

Вместе с элементом g в смежном классе {N(a)}g в общем случае имеются и отличные от g элементы группы Gn . Докажем замечательный факт: трансформирование элемента a лю-

бым (в общем случае отличным от a и g) элементом x из сме-

жного класса {N(a)}g может дать в качестве сопряжённого с a элемента только тот же элемент b и никакой другой:

x–1a x = b, x {N(a)}g.

( 2. 58 )

Действительно, из условия принадлежности элемента x к смежному классу {N (a)} g следует, что он может быть представлен в виде произведения x = h g, где h N (a). Подставив это

выражение x = hg в равенство (2.58 ), получим

x–1a x = (hg)–1a (hg) (1.23 ) (g–1h–1)a (hg) = g–1(h–1a) (hg) = = g–1(ah–1) (hg) = g–1a(h–1h)g = g–1a(εg) = g–1a g (2.58) b .

Здесь мы воспользовались принадлежностью элемента h, а значит и элемента h –1, к подгруппе N (a), что позволило применить равенство h –1a = a h –1 (все элементы, принадлежащие нормализатору N(a), коммутируют с элементом a).

Но пока ещё не доказано, что среди элементов, не принадлежащих смежному классу {N (a)} g, не найдётся такого элемента, который всё-таки мог бы трансформировать элемент a в элемент b. Допустив (от противного) существова-

ние такого элемента p	p {N(a)}g ,
p–1a p = b ,		( 2. 59 )

покажем несостоятельность этого допущения. Представим элемент p в виде p = pε= p (g–1g) = ( pg–1) g

71форумстудентов.рф72

и с учётом того, что ( pg –1) –1 = g p –1 (согласно (1.23 )), выполним трансформирование элемента a элементом ( pg–1):

( pg–1)–1a ( pg–1) = (g p–1)a ( pg–1) = g ( p–1a p) g–1 (2.59) g b g–1.

Но так как из исходного равенства (2.58) g–1a g = b следует g b g–1 = a ,

то мы получили

( pg–1)–1a ( pg–1) = a .

Этот результат равносилен равенству a ( pg–1) = ( pg–1) a ,

и означает, что элемент ( p g –1) коммутирует с элементом a,

т.е. принадлежит нормализатору N(a)
pg–1 N(a).	( 2. 60 )

Поэтому произведение элемента pg –1 на элемент g принадлежит смежному классу {N(a)}g и мы приходим к результату

( pg–1) g = p (g–1g) = pε = p {N(a)}g,

( 2. 61 )

опровергающему допущение (2.59).

Итак, мы доказали, что если элемент g Gn , принадлежащий смежному классу {N(a)}g по нормализатору N(a) элемента a, трансформирует элемент a в элемент b, то и все без исключения элементы смежного класса {N(a)} g будут трансформировать элемент a в тот же элемент b, и ни в какой другой. И обратно, всякий элемент p, трансформирующий элемент a в элемент b, по необходимости принадлежит смежному классу {N(a)}g. Это означает, что существует взаимно од-

нозначное соответствие между правыми смежными клас-

сами по нормализатору N(a) и элементами, сопряжёнными с а: каждому из элементов, сопряжённых с a, соответствует один и только один из непересекающихся смежных классов по нормализатору N (a). Иначе говоря, различных между собой, но сопряжённых с элементом a элементов в группе Gn ровно столько, сколько в ней непересекающихся правых смежных классов по нормализатору N (a). А так как число непересекающихся правых смежных классов по подгруппе N (a) равно индексу i подгруппы, который согласно теореме 2.6

(равенству (2.31)) в начале § 5 гл. 2, является делителем порядка группы Gn , то и число элементов, сопряжённых с элементом a, является делителем порядка группы Gn . По смыслу проведённого доказательства элемент a служит представителем любого произвольно взятого элемента группы Gn , и так как этим элементом однозначно определяется класс сопряжённых с ним элементов, то мы доказали, что число элементов в каждом классе сопряжённых элементов группы Gn является делителем порядка группы.

Замечание 4. В свете теоремы 2.12 становится понятен тот отмеченный в замечании 3 факт, что в группе вращений тетраэдра (имеющей порядок 12), не попадают в один класс сопряжённых элементов повороты вокруг четырёх осей третьего порядка на минимальный угол 2π / 3 и повороты вокруг тех же осей на двойной минимальный угол. Такой класс содержал бы в себе 8 элементов, а это невозможно, поскольку число 8 не является делителем порядка 12 группы вращений тетраэдра. Но полная группа симметрии тетраэдра имеет порядок 24, и в ней все 8 указанных поворотов попадают в один

итот же класс сопряжённых элементов.

§10. СОПРЯЖЁННЫЕ ПОДГРУППЫ.

Теорема 2. 13. Если H — подгруппа группы G, то результат сопряжения подгруппы H любым элементом aG, т.е. подмножество

a–1Ha = {a–1h a: h H } ,

( 2. 62 )

тоже является подгруппой, которую называют сопряжённой с подгруппой H.

Доказывается это с помощью двух достаточных признаков подгруппы (теорема 2.1 в начале §1 гл. 2).

1) Пусть элементы hi , hk принадлежат подгруппе H, и следовательно их произведение hi hk принадлежит H. Тогда эле-

73форумстудентов.рф74

менты a –1hi a и a –1hk a принадлежат подмножеству a –1H a

(2.62) и их произведение

(a–1hi a) (a–1hk a) = a–1hi (aa–1)hk a = a–1 (hi hk) a

принадлежит a–1Ha, потому что hi hk H.

2) Пусть h H (и следовательно h –1 H ). Тогда вместе с элементом a –1h a a –1Ha и обратный элемент (a –1h a) –1 при-

надлежит подмножеству a–1Ha:

(a–1ha)–1 = a–1h –1a a–1Ha ,

так как h –1 H.

Понятие сопряжения подгрупп позволяет дать другую формулировку необходимому и достаточному признаку нормальности подгруппы, отличному от признака (2.38).

Теорема 2.14 (второй необходимый и достаточный признак нормальности подгруппы). Для того что-

бы подгруппа H группы G была нормальной, т.е. чтобы выполнялось условие (2.37) из определения 2.7 (конец § 5 гл. 2), не-

обходимо и достаточно, чтобы она совпадала с любой соп-

ряжённой с ней подгруппой, т.е. чтобы выполнялось условие

a–1Ha = H , a G .

( 2. 63 )

Необходимость. Исходим из того, что подгруппа H нормальная. Тогда для неё выполняется первый необходимый и достаточный признак (2.38) нормальности

aH = Ha , a G ,

( 2. 64 )

из которого следует (2.63)

H = a–1Ha .

Достаточность. При доказательстве достаточности ус-

ловия (2.63) исходим из того, что оно выполнено. Тогда из не-

го следует (2.64): H = a–1Ha = H = a–1(Ha)

Ha = aH ,

чтослужитдостаточнымусловиемнормальностиподгруппы.

Взаключение главыоструктурных подмножествахгруппы рассмотрим представление группы в виде прямого произведения её нормальных подгрупп.

§ 11. ПРЯМОЕ ПРОИЗВЕДЕНИЕ ПОДГРУПП.

О п р е д е л е н и е 2. 10. Группа G называется прямым произведением своих подгрупп A и B (обозначение (G = A B), если выполнены 3 условия:

1)подгруппы A и B нормальные;

2)A ∩B = ε — пересечение подгрупп A и B состоит только из нейтрального элемента группы;

3)каждый элемент g G может быть представлен в виде произведения g = ab, где a A, b B.

Теорема 2.15. Если группа G является прямым

произведением своих подгрупп G = A B, т.е. если выполнены все три условия определения 2.10, то

I ) каждый элемент g G = A B представляется в виде g =

=ab однозначно (a A, b B);

II ) каждый элемент a A коммутирует с каждым элеме-

нтом b B.

Доказательство утверждения I. Допустим противное,

будто для некоторого элемента g G возможны различные представления в виде произведений

	g = ai bi ,		g = ak bk ,		где ai ≠ ak ,			bi ≠ bk ,	( 2. 65 )
что позволяет написать равенство
			ai bi = ak bk .						( 2. 65 )
Умножив это равенство справа наb 1						и слева на a 1 , получим
					i			k
a 1	(ai bi) b 1	= a 1	(ak bk) b 1	a 1 ai (bi b 1 ) = ( a 1 ak) bk b 1 ,
k	i	k	i		k		i	k	i
что равносильно равенству
			a 1 ai		= bk b 1	,			( 2. 66 )
			k		i
где	a 1 ai A,		bk b 1 B.		Согласно (2.66) элемент a 1 ai
	k		i						k
принадлежит также подгруппе B (и bk b 1							принадлежит A). Но
						i

75форумстудентов.рф76

так как по условию 2) из определения 2.10 подгруппы A и B пересекаются только по нейтральному элементу ε группы G (не имеют иных общих им элементов, кроме ε), то

ak1 ai = ε,		откуда следует	ai = ak ,
bk b 1	= ε,	откуда следует	bk = bi .
i

Этим опровергнута возможность совместного выполнения условий (2.65), (2.65 ) и доказана однозначность представления любого элемента g группы G в виде произведения g = ab.

Доказательство утверждения II. Составим произве-

дение элементов
a–1b–1a b ,	( 2. 67 )

называемое коммутатором элементов a и b, и представим его в двух записях

a–1b–1a b = (a–1b–1a) b ,	( 2. 67 )
a–1b–1a b = a–1(b–1a b) .	( 2. 67 )

Так как b –1 B, то элемент (a –1b –1a) из (2.67 ) принадлежит подгруппе a–1Ba, сопряжённой с подгруппой B. Но так как по условию теоремы 2.15 и определению 2.10 подгруппа B нормальная, то она совпадает с a –1B a согласно теореме 2.14 (о втором признаке нормальности подгруппы), и потому

(a–1b–1a) B , а значит a–1b–1a b = (a–1b–1a)b B . ( 2. 68 )

Аналогичным образом из принадлежности элемента a подгруппе A следует, что элемент (b –1a b) принадлежит подгруппе b –1A b, сопряжённой с A. Но так как подгруппа A нормальная, то она совпадает с подгруппой b–1Ab, и потому

(b–1a b) A , а значит a–1b–1a b = a–1(b–1a b) A . ( 2. 68 )

И так как A ∩ B = ε (по условию 2) из определения 2.10 ), то

мы получаем из (2.68), (2.68 )

a–1b–1a b = (ba)–1(a b) = ε,

откуда следует

ba = a b ,

что и требовалось доказать.

Замечание. Так как подгруппы A и B в прямом произведении A B = G имеют только один общий им элемент, а именно нейтральный элемент ε, присутствующий в каждой группе, то число элементов в группе G = A B равно произведению порядков подгрупп A и B. Действительно, пусть подгруппа A имеет порядок k, а подгруппа B — порядок m. Умножая нейтральный элемент ε последовательно на каждый из m элементов подгруппы B, получим m произведений. Остальные k – 1 элементов подгруппы A при умножении на элементы подгруппы B дадут (k – 1) m произведений. Суммарное число произведений равно m + (k – 1) m = k m. Среди этих произведений нет одинаковых, так как в противном случае оказалось бы, что хотя бы один из элементов группы G представлен в виде произведения ab, a A, b B не однозначно в противоречии с утверждением I ) теоремы 2.15.

Пример.

Вклейновской группе G4(1) 4-го порядка (см. таблицу (1.41)

вконце §7 гл.1) подгруппы {ε, a} и {ε, b} второго порядка являются нормальными, как все подгруппы индекса i = 2 (см. замечание 2 в конце § 5 гл. 2). Пересечение этих подгрупп состоит только из нейтрального элемента ε, и каждый элемент группы G4(1) {ε, a, b, c} является произведением указанных

подгрупп: ε= εε, a = a ε, b = εb, c = a b. Все три условия определения 2.10 выполнены.

Задание № 7. Найти два представления группы симметрии треугольного диэдра в виде прямых произведений её нормальных подгрупп.

Возникает вопрос: нельзя ли из произвольно взятых групп A и B построить такое множество G, которое было бы группой, и по отношению к которому группы A и B или изоморфные им соответственно группы GA и GB (ибо абстрактная группа служит представителем всего множества изоморфных между собой групп) играли бы роль нормальных подгрупп, прямое произведение которых равно группе G.

77форумстудентов.рф78

Для этого потребуется так определить операцию перемножения групп A и B, чтобы каждый элемент искомого множества G формировался с непременным участием элементов ai и bk групп A и B. Этому требованию не могут удовлетворить операции, определённые на каждой из групп A и B в отдельности. Ведь операция группы A ставит в соответствие любым элементам группы A элемент этой же группы и не предопределяет сама по себе, как надо умножать элемент ai на элемент bk. По смыслу поставленной задачи каждый элемент множества G должен определяться парой (ai , bk) элементов групп A и B. Если определить умножение таких пар равенством

(ai , bk)(ap , bq) = (aiap , bk bq) ,

( 2. 69 )

то в каждом произведении будет представлен элемент ai ap группы A и элемент bk bq группы B. Обозначив нейтральные элементы групп A и B символами aо и bо соответственно, и учитывая, что aоaо = aо, bоbо = bо, можно утверждать, что элемент

(aо, bо)(aо, bо) = (aоaо, bоbо) = (aо, bо)

( 2. 70 )

будет играть роль нейтральной пары при перемножении (2.69) пар:

(ai , bk)(aо, bо) = (ai aо, bk bо) = (ai , bk) .

( 2. 70 )

Легко убедиться, что правило (2.69) удовлетворяет требованиям определения1.1 бинарной алгебраической операции (см. §1 гл. 1). Эта операция ассоциативна (в силу ассоциативности операций на группах A и B):

{(ai , bk)(ap , bq)}(as , bt) = (ai ap , bk bq)(as , bt) = {(ai ap)as , (bk bq)bt} =

= {ai (ap as), bk (bq bt)} = (as , bt){(ai , bk)(ap , bq)} .

( 2. 71 )

В формулах (2.70), (2.70 ) отражено выполнение второй аксиомы группы (о нейтральном элементе). Наконец, для каждой пары (a , b) из множества G найдётся в этом множестве обратная пара (a, b)–1 = (a–1, b–1),

удовлетворяющая третьей аксиоме группы:

(a, b)(a, b)–1 = (a, b)(a–1, b–1) = (aa–1, bb–1) = (aо, bо) . ( 2. 72 )

Так как в равенствах (2.69), (2.71), (2.70), (2.72) выражено выполнение всех требований определения группы, то множество G пар (ai , bk) элементов групп A и B является группой.

Так как в произведении пар (ai , bо) (ak , bо) = (ai ak , bо) левый элемент выступает в роли представителя любых элементов группы A и этот элемент способен изменяться только при изменении элементов группы A, тогда как правый элемент bо B пары фиксирован и не зависит от группы A, то определено взаимно однозначное отображение

f (ai) = (ai , bо) GA , f (A) = GA G ( 2. 73 )

группы A на подмножество GA группы G. Легко доказать (по достаточному и необходимому признаку подгруппы (§1 гл. 1)), что GA есть под-

группа группы G. При этом выполняется требование (1.31) сохранения операции при отображении (2.73), последнее, следовательно, является

изоморфизмом:

f (ai) f (ap) = (ai , bо)(ap , bо) = (ai ap , bo bo) = (ai ap , bo) = f (ai ap) .

Аналогичным образом равенства
φ (bk) = (aо, bk) GB ,		φ (B) = GB G	( 2. 73 )

определяют изоморфное отображение группы B на подгруппу GB G. Теперь докажем с помощью второго необходимого и достаточного признака (2.63) в конце § 11 гл. 2, что подгруппа GA группы G яв-

ляется нормальной. Пусть g = (a , b) — произвольный элемент группы G. Согласно (2.72) g–1= (a, b)–1= (a–1, b–1). Выполним сопряжение про-

извольного элемента (ai , bо) подгруппы GA (см. (2.73)) элементом g:
g–1(ai , bо) g = (a–1, b–1)(ai , bо)(a, b) = (a–1ai a, b–1bо b) =
= (a–1ai a, b–1b) = (a–1ai a , bо) .	( 2. 74 )

Так как в левой части цепочки равенств (2.74) записан произвольный элемент подгруппы g– 1GA g, сопряжённой произвольным элементом g с подгруппой GA , а правая часть показывает, что в результате такого сопряжения может получиться только элемент (a – 1ai a , bо) типа (ap , bо), принадлежащий подгруппе GA , то равенство (2.74) доказывает нормальность подгруппы GA в группе G. Аналогично доказывается нормальность подгруппы GB , изоморфной группе B.

Подведём итоги. Правилом (2.69) определена операция, которая ставит в соответствие элементам произвольно взятых групп A и B элементы (a , b) группы G. В группе G, построенной таким способом, есть нормальные подгруппы GA и GB , изоморфные соответственно группам A и B. При этом любой элемент (a , b) группы G может быть представлен в виде произведения элементов (a , bо) GA и (aо , b) GB

по правилу (2.69):
(a, bо)(aо, b) = (aao , bo b) = (a, b) .	( 2. 75 )
Наконец, пересечение подгрупп GA и GB состоит	только из ней-

трального элемента (aо , bо) группы G, ибо элементы (a , bо) и (aо , b)

подгрупп GA и GB могут совпадать друг с другом
(a, bо) = (aо, b)	только в случае	a = aо , bо = b .

Значит выполнены все три требования определения 2.10 (см. начало §11 гл. 2) и мы построили группу G = GA GB , являющуюся прямым произведением своих подгрупп GA и GB , которые совпадают с точностью до изоморфизмов с группами A и B соответственно.

79форумстудентов.рф80