МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Московский государственный университет тонких химических технологий им. М.В.Ломоносова

Кафедра высшей и прикладной математики

Л.М. Ожерелкова, А.Г. Рубин, И.А. Джемесюк

Ряды

Учебно-методическое пособие

Москва 2012

УДК 51

ББК 22.1

Рецензент – доктор физ.-мат.наук, профессор Карташов Э.М.

Л.М. Ожерелкова, А.Г. Рубин, И.А. Джемесюк Ряды. Учебно-методическое пособие. М.: ИПЦ МИТХТ, 44 с.

Утверждено библиотечно-издательской комиссией в качестве учебно-методического пособия для студентов 2–4-го курсов дневного отделения

всех специальностей МИТХТ им. М.В.Ломоносова по дисциплине «Высшая математика», поз. /2012.

МИТХТ им. М.В.Ломоносова, 2012

2

§1. Основные понятия

Определение. Числовым рядом называется бесконечная последовательность чисел u1, u2 , K , un ,K , соединенных знаком

сложения:

∞
u1 + u2 +K + un +K = ∑un .	(1.1)
n=1
Числа u1, u2 , K , un ,K называются членами ряда, а член	un –

общим или n-м членом ряда.

Ряд (1.1) считается заданным, если известен его общий член un = f (n) , ( n =1,2,K ), т.е. задана функция f (n) натурального

	аргумента.			Например,			ряд с общим членом u =			(−1)n+1	имеет
										n 2n
									n
	вид:	1	−	1	+	1	−K +	(−1)n+1	+K
				2 22		3 23		n 2n
		1 2

Образуем новую последовательность:

S1 = u1

S2 = u1 +u2

………………..

Sn = u1 + u2 +K + un

Определение. Сумма n первых членов ряда называется n-ой частичной суммой ряда и обозначается Sn .

Определение. Если последовательность частичных сумм ряда имеет предел, то такой ряд называется сходящимся, а этот предел называется суммой ряда.

То есть, если lim Sn = S , то ряд сходится, а	S – сумма ряда.
n→∞
∞
В этом смысле можно записать ∑un = S .
n=1

Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся. У расходяще-

3

гося ряда суммы нет.

Пример 1. Исследовать на сходимость геометрический ряд, т.е. ряд, составленный из последовательных членов геометрической прогрессии:

		∞
a + aq + aq2	+K + aqn−1	+K = ∑aqn−1	(1.2)

n=1

Решение. Необходимо установить, при каких значениях знаменателя прогрессии q ряд (1.2) сходится, а при каких – расхо-

дится. Из школьного курса алгебры известно, что сумма первых n членов геометрической прогрессии, т.е. n-я частичная сумма

ряда при q ≠1

равна Sn =

a(1 − qn )

.

1

− q

Возможно несколько случаев:

1) если

q

<1, то lim qn = 0

n→∞

n

a

aq

a

и lim Sn = lim

−

=

, т.е. ряд сходится и его сумма

1− q

1− q

n→∞

n→∞

1− q

S =

a

.

1− q

2)

если

q

>1,

то

lim qn = ∞ и, следовательно, lim Sn = ∞, и

n→∞

n→∞

ряд расходится.

3) если q =1, то ряд (1.2) примет вид a + a + a +K + a +K ,

	его S	n	= a + a + a +K + a = na			и lim S	n	= lim na = ∞, ряд рас-
			14444444244444443			n→∞		n→∞
				nраз
	ходится.
	4)		если	q = −1,	то	ряд		(1.2)	примет		вид
	a − a + a − a +K + (−1)n a +K ,					и его		Sn = 0	при n	четном и
	Sn = a при n нечетном, следовательно, lim Sn								не существует, и
	ряд расходится.							n→∞
										a
	Т.о.		геометрический		ряд сходится			к сумме S =			при
										1− q

4

q<1 и расходится при q ≥1. Пример 2. Найти сумму ряда:

	1	+	1		+	1	+K +	1		+K
						3 4		n (n	+1)
1 2 2 3

Решение. n -я частичная сумма ряда:

Sn =

1

+

1

+

1

+K +

1

3 4

n (n +1)

1 2 2 3

Учитывая, что

1

=1−

1 ,

1

=

1

− 1

,

1

=

1 − 1 ,...,

1

= 1

−

1

,

2 3

3 4

n (n +1)

(n +1)

1 2

2

2 3

3 4

n

частичную сумму ряда можно представить в виде

n

1

1

1

1

1

1

1

1

Sn = 1 −

+

−

+

−

+K

+

−

=

1 −

=

,

3

3

4

n +1

n

+1

2

2

n

n +1

и тогда получаем:

lim S

n

= lim

n

=1, т.е. сумма ряда S =1.

n→∞

n→∞ n +1

Свойства сходящихся рядов

Свойство 1. Если ряд u1 + u2

+K + un +K

сходится и имеет

сумму S , то и ряд

cu1 + cu2 +K + cun

+K ,

полученный умно-

жением данного ряда на число c , также сходится, и имеет сумму

cS .

∞

∞

Свойство 2. Если ряды ∑un

и ∑vn

сходятся и их суммы

n=1

n=1

∞

соответственно равны S1 и S2 , то и ряды ∑(un ± vn ) также схо-

n=1

дятся и их суммы равны соответственно (S1 + S2 ) и (S1 − S2 ) .

Свойство 3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или добавления) конечного числа членов.

Установить сходимость (расходимость) ряда путем нахожде-

ния частичной суммы Sn и вычисления lim Sn , как это сделано в

n→∞

5

примерах 1 и 2, возможно лишь в редчайших случаях из-за принципиальных трудностей при нахождении Sn (суммирова-

нии первых n членов ряда). Обычно сходимость (расходимость) ряда устанавливается с помощью специальных теорем – признаков сходимости.

В большинстве признаков сходимости вам придется вычислять некоторый предел. Напомним кратко два основных приема вычисления пределов, которыми вы будете пользоваться чаще всего.

А) Предел отношения двух степенных выражений на бесконечности равен:

0, если степень числителя меньше степени знаменателя; ∞, если степень числителя больше степени знаменателя;

отношению старших коэффициентов, если степень числителя равна степени знаменателя*.

Б) Правило Лопиталя. Предел отношения двух бесконечно малых величин (б.м.) или двух бесконечно больших величин (б.б.) равен пределу отношения их производных. Например, по правилу Лопиталя имеем:

lim ln(x +3)		(ln(x +3))′			1				x +2
	= lim		= lim		x +3			= lim		=1
					1
x→∞ ln(x +2)	x→∞	(ln(x +2))′	x→∞					x→∞ x +3
					x +2

§2. Признаки сходимости знакопостоянных рядов

I. Необходимый признак сходимости рядов

Необходимым признаком сходимости рядов является следу-

* Напомним, что степенью степенного выражения называется наибольшая из степеней входящих в него слагаемых, само это слагаемое называется старшим, а его коэффициент называется старшим коэффициентом. Например, у

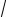степенного выражения 2n −3n +5nn +4 старшее слагаемое (т.е. 5n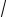n ) имеет степень 1,5, а старший коэффициент равен 5.

6

ющая теорема.

Теорема. Если ряд сходится, то предел его общего члена un

при n → ∞ равен нулю, т.е. limun = 0 .

n→∞

Однако на практике в таком виде применять теорему для исследования ряда невозможно, т.к. мы не знаем, сходится ли наш ряд. Поэтому для практического применения необходимый признак сходимости сформулируем в следующем виде:

Следствие. Если предел общего члена ряда при n → ∞ не равен нулю, то ряд расходится.

	Пример. Исследовать на сходимость ряд							∞	2n +5
								∑n=1	3n − 2
				2n +5		2
	Решение. Т.к. limu	n	= lim		=		≠ 0 , то ряд расходится
	n→∞		n→∞	3n − 2		3

(по необходимому признаку сходимости).

Очень важно помнить, что из того, что limun = 0 , не следует

n→∞

ни сходимость, ни расходимость ряда. Говорят, что если

limun = 0 , то необходимый признак не работает.

n→∞

Замечание. Смысл или польза этого признака: если общий член ряда стремится к нулю, то ряд может быть как сходящимся,

так и расходящимся, а если limun ≠ 0 , то это заведомо расходя-

n→∞

щийся ряд. Этот признак является необходимым, но не достаточным.

В качестве примера рассмотрим ряд

1 +	1	+	1	+	1	+K +	1	+K ,	(2.1)
	2		3		4		n

называемый гармоническим.

Необходимый признак сходимости для этого ряда не работа-

ет, т.к. limu	n	= lim 1	= 0 . Докажем, что ряд расходится.
n→∞		n→∞ n

Перепишем ряд (2.1) в виде:

7

1 +	1		1				1				1					1				1		1							1					1												1								(2.2)
		+				+				+				+					+		+					+				+								+K					+						+L
	2				3							5				6				7		8							9			10												16
							4
			1442 443								14444442 4444443																	144444442 44444443
					2члена													4члена																	8членов
Напишем вспомогательный ряд:
1 +	1		1				1				1						1			1		1							1					1												1								(2.3)
		+				+				+				+					+		+					+					+									+K			+								+L
	2				4							8					8			8		8												16
							4																					16																		16
			14442 4443								14444442 4444443																	1444444442 444444443
					2члена													4члена																		8членов
Ряд (2.3) строится так, что каждый его член меньше либо ра-
вен соответствующему члену ряда (2.2).
Обозначим через Sn(1) сумму n первых членов ряда (2.2), и
через Sn(2)				частичную сумму ряда (2.3).
Т.к. каждый член ряда (2.2) больше либо равен соответству-
ющему ему члену ряда (2.3), то
Sn(1) > Sn(2) .																																																						(2.4)
Вычислим несколько частичных сумм ряда (2.3) для значений
n , равных 21 , 22 , 23 , 24 , 25 ,..., 2k ,... :
S2 =1 +					1	=1 +1					1
					2						2
S4 =1 +				1		+		1	+		1			=1 + 2							1
					2			4			4										2
							14442 4443
									12
S8 =1 +				1		+		1	+		1		+					1	+	1	+		1	+			1		=1 + 3											1
				2				4			4							8		8			8																	2
																											8
							14442 4443								14444442 4444443
									12												12
………………………………………………………….
					1			1			1							1		1		1					1									1															1				1
S2k =1 +						+				+				+					+		+			+					+K					+								+K +											=1 + k			,
					2			4			4							8		8		8					8												2		k								2			k			2
							14442 4443									14444442 4444443																				14444442 4444443
										12											12																						12
следовательно,								lim S															1		k				= ∞, а тогда в силу (																									2.4)
													k		= lim 1+								2
								k	→∞			2						k	→∞

8

lim S (1) = ∞ , и ряд (2.1) расходится.

k→∞ n

Далее рассмотрим достаточные признаки сходимости знакоположительных рядов.

II. Признак Даламбера

	∞
Теорема.	Пусть для ряда ∑un	( un > 0 ) существует предел
	n=1

отношения (n +1)-го члена ряда к n -му: lim un+1 = L . Тогда:

n→∞ un

а) если L <1, то ряд сходится,

б) если L >1, то ряд расходится,

в) если L =1, то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает.

Примеры

Исследовать следующие ряды на сходимость:

∞

n +

2

1) ∑

.

Решение. Т.к.

n

n=1

3

u

n + 3

n +

2

n + 3

3n

n + 3

1

lim

n+1

= lim

n+1

:

n

= lim

n+1

= lim

=

<1,

n + 2

3(n + 2)

3

n→∞

u

n→∞

3

3

n→∞

3

n→∞

n

то по признаку Даламбера ряд сходится.

∞

2

+1

2) ∑n

n=1

n!

Замечание.

Напомним,

что n! =1 2 3K n ,

поэтому 1! =1,

2!=1 2 = 2,

3!=1 2 3 = 6,K , (n +1)!=1 2 K n (n +1) = n! (n +1) .

144424443

n!

Решение. Воспользуемся формулой (n +1)!= n! (n +1) , тогда:

lim

u

= lim

(n

+1)2

+1

:

n2 +1

= lim

n2

+ 2n +

2

n!

=

n

+1

(n +1)!

n!

(n +

1)!

n

2

+1

n→∞

u

n

n→∞

n→∞

= lim

n2

+ 2n + 2

= 0 <1,

(n +1)(n2

+1)

n→∞

9

следовательно, по признаку Даламбера ряд сходится.

3) ∑∞ 5n nn!

n=1 n

Решение

un+1

5n+1 (n +1)!

nn

5n!(n +1)

nn

lim

=

n+1

n

n

un

= lim

(n +1)

5

= lim

(n +1)

(n +

1)

n→∞

n→∞

n!

n→∞

n!

= lim

5nn

= lim

5

= lim

5

=

5

>1

n

1

n

e

n→∞ (n +1)n

n→∞ n +1

n→∞

+

n

1

n

и ряд расходится.

Замечание. С помощью признака Даламбера исследовать ряды на сходимость имеет смысл только тогда, когда в выражении для n - го члена ряда имеются показательная функция и/или факториал.

III. Радикальный признак Коши

∞

Теорема. Пусть для ряда ∑un , ( un > 0 ) существует

n=1

lim n un = L . Тогда

n→∞

а) если L <1, то ряд сходится,

б) если L >1, то ряд расходится,

в) если L =1, то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает.

Примеры. Исследовать следующие ряды на сходимость:

1) ∑∞ 3n −1 n n=1 2n +3

Решение. Вычислим

3n −1 n

3n −1

3

lim n un

, следовательно,

= lim n

= lim

=

>1

2n +3

2n +3

2

n→∞

n→∞

n→∞

по радикальному признаку Коши ряд расходится.

10

∞
2) ∑arctg n 1
n=1		n
Решение. Вычислим
		= lim n				1
lim n			arctg n 1		= lim arctg		= 0 <1, следовательно,
	un
n→∞		n→∞		n	n→∞	n

по радикальному признаку Коши ряд сходится.

Замечание. С помощью радикального признака Коши исследовать ряды на сходимость имеет смысл тогда, когда n -й член ряда представляет собой некое выражение, возведенное в n -ю степень.

IV. Интегральный признак Коши

∞

Теорема. Пусть члены ряда ∑un положительны и пусть

n=1

f (x) такая непрерывная функция, что f (1) = u1 , f (2) = u2 , … f (n) = un , …, причем функция f (x) невозрастающая на интервале [x0 ; +∞) при некотором x0 . Тогда справедливы следующие утверждения:

1) если несобственный интеграл	∞∫ f (x)dx сходится, то схо-
	1
∞
дится и ряд ∑un ,
n=1

2) если несобственный интеграл ∞∫ f (x)dx расходится, то рас-

1

∞

ходится и ряд ∑un .

n=1

Для краткости говорят: «Ряд и интеграл ведут себя одинаково». Замечание. Для применения интегрального признака к исследо-

∞

ванию сходимости ряда ∑un надо подобрать такую функцию

n=1

11

f (x) , что f (n) = un , (n =1,2,....) , т.е. попросту говоря, выписать un и заменить в нем n на x, и затем исследовать сходимость ин-

теграла ∞∫ f (x)dx . Это имеет смысл делать только тогда, когда

1

полученный интеграл достаточно легко вычисляется.

Примеры

1) Применим интегральный признак к исследованию на схо-

∞

1

димость ряда вида ∑

, p > 0 ,

называемого обобщенным гар-

p

n=1

n

моническим рядом или рядом Дирихле.

Решение. В этом

случае

требуемой

функцией является

f (x) =

1

. Функция

f (x) =

1

является

невозрастающей на

x p

x p

интервале [1; +∞) . Вычислим ∞∫

dxp .

1

x

Если p =1, то +∞∫dx

=ln

x

1+∞

= ln

+ ∞

−ln1 = ∞.

1 x

+∞dx

x−p+1

+∞

1

при p >1

Если p ≠1, то

∫1 x

=

= p −1

.

− p +

1

1

∞ при p <1

Следовательно, несобственный интеграл сходится при p >1 и расходится при 0 < p ≤1. То же самое можно сказать и о данном ряде.

				∞	1
			Запомнить! Обобщенный гармонический ряд ∑			сходит-
					p
	ся при p >1 и расходится при p ≤1.			n=1	n
			∞
			2) Исследовать на сходимость ряд ∑ln n .
			n=1	n

12

Решение. Выписав un = lnnn и заменив в нем n на x, получим функцию f (x) = lnxx .

Внимание! Пока мы не убедились, что функция невозрастающая на некотором интервале вида [x0 ; +∞) , к интегрированию

переходить рано!

Исследуем функцию f (x) = lnxx на монотонность с помощью

		1	x −1 ln x		1 − ln x
производной: f	′	x
				= x2 . Критическая точка
			x2
	(x) =
x = e , на интервале x [e; +∞) f				(x) ≤ 0 , т.е. функция f (x) не-
				′

возрастающая. Теперь можно переходить к интегрированию.

+∞		+∞		+∞
∫ln x dx =		∫ln xd ln x = ln2 x		= ∞, интеграл расходится,
1	x	1	2	1

расходится и данный ряд.

V. Признаки сравнения

Теорема. Первый признак сравнения (признак сравнения в форме неравенства). Пусть даны два ряда с положительными членами:

u1 +u2	+....	+un +...	(2.5)
v1 + v2	+....	+ vn +...	(2.6)

причем члены первого ряда не превосходят членов второго при любом n , т.е.

un ≤ vn

(2.7)

Тогда: а) если сходится ряд (2.6), то сходится и ряд (2.5)

б) если расходится ряд (2.5), то расходится и ряд (2.6).

Удобно применять другую формулировку этой теоремы:

а) если больший ряд сходится, то меньший ряд тоже сходится;

13

б) если меньший ряд расходится, то больший ряд тоже расходится.

Примеры

Исследовать сходимость следующих рядов:

1) ∑		1
∞
n=2		n(n −1)
				∞		, мыс-
Решение. Сравним данный ряд с гармоническим ∑1
				n=1	n

ленно отбросив его первый член, равный 1 (что, естественно, не

	повлияет на сходимость ряда). Т.к.										1			>		1	,		1		>	1	, и в о-
																2						3
											2 1								3 2
			1			1
	обще,				>		(ведь		<			n2			= n ), то члены данно-
								n(n −1)
						n
			n(n −1)

го ряда больше членов расходящегося гармонического ряда, и, следовательно, на основании признака сравнения данный ряд расходится.

Понятно, что для применения признака сравнения в форме неравенства нужно сначала установить подходящее неравенство. При этом часто пользуются следующими стандартными неравенствами:

ln x < x, x (0; +∞) ,			(2.8)
−1	≤ sin x ≤1,	x Ў ,
−1	≤ cos x ≤1,	x Ў .

Иногда приходится применять более сложные неравенства:

−	π	≤ arcsin x ≤ π	,	x [−1;1] ,
	2	2		x [−1;1] ,
	0 ≤ arccos x ≤ π,
−	π	≤ arctg x ≤ π ,		x Ў ,
	2	2		x Ў ,
	0 ≤ arcctg x ≤ π,
ln x < x p , p > 0,				x (x ; +∞)	при некотором x .
				0	0

14

2) ∑∞ sin4 (2n + 3)

n=1 n3

Решение. Прежде всего, заметим, что это ряд с положительными членами, т.к. синус возводится в четную степень. Далее

очевидное неравенство sin4 (2n + 3) ≤1 позволяет заключить, что

sin4 (2n + 3)			1					∞	1
	3	≤			, а поскольку ряд			∑			сходится, то и ряд с
n			n	3					n	3
								n=1
					∞	sin4 (2n + 3)		тоже сходится.
меньшими членами ∑						n	3
					n=1

3) ∑∞ 1 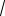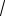(n +1 − n −1)

n=1 n

Решение. Преобразуем выражение, стоящее под знаком суммы, следующим образом:

1

1 (

−

+

(

−

n +1

n −1)(

n +1

n −1)

=

n +1

n −1) =

n

n

n +1 +

n −1

1

2

2

=

<

n ( n +1 + n −1)

n n

(здесь мы учли, что (

+

n +1

n −1) > n +1 > n ).

∞

1

Т.к. ряд ∑

– сходится (как обобщенный гармонический

3 2

n=1

n

при p >1), то исследуемый ряд также сходится.

Отметим «эталонные» ряды, часто используемые для сравнения:

∞

а) геометрический ряд ∑aqn−1 – сходится при

q

<1, расхо-

n=1

дится при

q

>1,

1

∞

б) обобщенный гармонический ряд ∑

сходится при

p >1

p

n=1

n

и расходится при p ≤1.

15

Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (2.7), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т. п.). Более простым оказывается признак сравнения в предельной форме – ведь вычислять пределы обычно гораздо проще, чем доказывать неравенства.

Теорема. Второй признак сравнения (признак сравнения в

∞ ∞

предельной форме). Если ∑un и ∑vn – ряды с положитель-

n=1 n=1

ными членами и существует предел отношения их общих членов

lim un = k , причем k ≠ 0, k ≠ ∞ , то ряды ведут себя одинаково:

n→∞ vn

либо одновременно сходятся, либо одновременно расходятся. Чаще всего исследуемый ряд сравнивают с обобщенным гар-

моническим рядом ∑∞ 1p , причем p удобно подбирать в процес-

n=1 n

се сравнения, как это сделано ниже в примере 1.

Примеры

∞	2	4+ n + 7
1) ∑2n	n
n=1		+ 3

Решение. Сравним данный ряд с обобщенным гармоническим

рядом ∑∞ 1p , причем p подберем в процессе сравнения.

n=1 n

Выпишем предел lim un и преобразуем его:

n→∞ vn

2n2 + n + 7

1

(2n2 + n + 7) n p

(2.9)

lim

4

:

= lim

4

n

+ 3

n

p

n

+ 3

n→∞

n→∞

Мы пришли к пределу отношения двух степенных выражений на бесконечности. Если степень числителя меньше степени зна-

16

менателя, то предел равен 0, а это тот случай, когда признак сравнения в предельной форме не работает. Если степень числителя больше степени знаменателя, то предел равен ∞, а это опять тот случай, когда признак сравнения в предельной форме не работает. Таким образом, нас устроит только случай, когда степень числителя равна степени знаменателя, т.е. p + 2 = 4 , или

p = 2 (в этом случае предел равен отношению старших коэффициентов, т.е. не 0 и не ∞). Итак, исследуемый ряд ведет себя так

	∞	1
	же, как и ряд ∑		, т.е. сходится.
		2
	n=1	n

Разумеется, решение похожих задач не надо расписывать так подробно. Обычно, выписав предел (2.9), далее пишут p + 2 = 4 p = 2 сходится. Ясно, что слово «сходится» от-

	∞	1
	носится сразу к двум рядам и к ∑		, и к исходному ряду.
		2
	n=1	n

Следствием второго (предельного) признака сравнения является третий признак сравнения.

Теорема. Третий признак сравнения (признак сравнения в форме эквивалентных б.м. или кратко эквивалентный признак сравнения). В общем члене ряда бесконечно малый множитель или делитель можно заменить на эквивалентный, поведение ряда (сходимость или расходимость) от этого не изменится.

Замечание 1. Напомним таблицу эквивалентных бесконечно малых величин (при t → 0 ):

sin t : t, arcsin t : t, tg t : t, arctg t : t, ln(1+t) : t .

Замечание 2. При работе с эквивалентным признаком сравнения необходимо помнить, что таблица эквивалентных бесконечно малых величин выписана при t → 0 , а в рядах всегда n → ∞, т.е. n является бесконечно большой. А вот б есконечно

малыми являются величины вида:							1	,	1	,		1			(и вообще	1
							n		n2							n p
													n
	1		1		1
при p > 0 ),		,		(и вообще		при a >1).
	n		n		n
	2		3		a

17

∞

1

2)

∑

ln 1

+

n=1

n

Решение.

Т.к. при

n → ∞

1

→ 0 (т.е.

1

– б.м.),

то

n

n

1

1

∞

1

ln

1

+

:

,

и ряд

∑

ln 1+

ведет себя так же, как и

n

n

n=1

n

∞

1

ряд

∑

– обобщенный гармонический ряд при p=1/2<1,

т.е.

n

n=1

расходится.

На практике запись ведут кратко:

∞

1

∞

1

∑ln

1

+

:

∑

– расходится. Ясно, что слово «расхо-

n=1

n

n=1

n

дится» относится к обоим рядам.

∞

π

3)

∑(3n +1) sin

.

n

n=1

2

π

π

π

∞

π

Решение.

∑(3n +1)sin

Т.к.

0;

,то

sin

> 0, ряд

2

n

2

2

n

2

n

n=1

знакоположительный, и к нему можно применять эквивалентный

признак

сравнения.

Поскольку

π

– б.м.

при

n → ∞, то

2n

sin πn :

πn

и ∑(3n +1)sin πn :

= π∑3n +n

1 .

∑π(3nn+1)

∞

∞

∞

2

2

n=1

2

n=1

2

n=1

2

Последний ряд легко исследуется по признаку Даламбера (он сходится).

Несмотря на то, что предельный и эквивалентный признаки сравнения более просты по сравнению с признаком сравнения в форме неравенства, иногда без первого признака не обойтись. Покажем это на следующем примере, а заодно продемонстрируем, как надо рассуждать в общем и целом при исследовании рядов на сходимость.

18

4) ∑ 1
∞
n=1 ln(n +1)	1
Решение. Проверим необходимый признак: lim		= 0 –
n→∞ ln(n +1)

необходимый признак не работает. Попробуем применить признак Даламбера:

	u			1		1			ln(n +1)
lim		n+1	= lim		:			= lim		=1,
n→∞ un						ln(n +1)		n→∞ ln(n + 2)
			n→∞ ln(n + 2)

т.е. вопрос о сходимости ряда остается открытым. Этого следовало ожидать (см. замечание к признаку Даламбера).

Применим признак сравнения в предельной форме. Сравним данный ряд, например, с гармоническим рядом:

	u	n		1		1			n	= ∞,
lim			= lim		:			= lim
n→∞ vn						n		n→∞ ln(n +1)
			n→∞ ln(n +1)

т.е. ответа о сходимости ряда нет. Аналогичная картина наблюдается и при использовании других «эталонных» рядов.

Применим, наконец, признак сравнения в форме неравенства (первый признак сравнения). Сравним данный ряд с гармониче-

ским, у которого отброшен первый член: 12 + 13 +... + n 1+1 +......

Т.к. члены рассматриваемого ряда больше членов расходящегося

	гармонического	1	>	1		, что вытекает из неравенства
		ln(n +1)		n +1

(2.8), то данный ряд расходится.

Отметим, что для исследования сходимости данного ряда неприменим и интегральный признак, т.к. первообразная подынтегральной функции не является элементарной функцией, т.е. со-

	ответствующий неопределенный интеграл		dx	является
		∫ln(x +1)
	«не берущимся».

19

Задачи А) Исследовать ряды с помощью признака Даламбера:

∞

∞

5

n

∞

n

3

1. ∑n(2nn−1)

2. ∑

3. ∑

n

n

2

(n +1)!

n=1

3

n=1

2

n=1

∞

n!

∞

n

∞

1

4. ∑

5. ∑n

6. ∑

n

(2n +1)!

n=1

10

n=1

n!

n=1

B) Исследовать ряды с помощью радикального признака Коши:

∞

1

∞

n 1

∞

1

∞

n n

7. ∑

8.

∑arcsin

9. ∑

10. ∑

n

n

n

n

(n +1)

n=1

n=1

n=1 ln

n=1

2n +1

C) Исследовать ряды с помощью интегрального признака Коши:

∞

1

∞

1

∞

2

11. ∑

12. ∑

13. ∑

n ln n

3

n

2

n=2

n=2 n ln

n=1

1+ n

1+ n

1

∞

∞

14. ∑

15. ∑e n2

2

n=1 1+ n

n=1 n

D) Исследовать ряды с помощью признаков сравнения:

∞

2

+1

∞

∞

16. ∑

n

17. ∑ntg

π

18. ∑n2 sin

π

3

n

n=1

n

n=1

2

n=1

3

∞

n −

n −1

∞

4

n

3

− 25

∞

1

19. ∑

20. ∑

21. ∑

n

n +50

n(1+ n

2

)

=

=

=

n

1

n

1

n

1

Е) Исследовать ряды на сходимость:

∞

1

∞

1

22.

∑

23.

∑

(2n −1)2

2n−1

(n +1)(n + 4)

n=1

n=1

∞

3n

2

+ 2n

∞

π

25.

∑

26.

∑tg

3

n +3

n=1

n +5n −5

n=1

∞

n

2

∞

5n + 6

28.

∑

29.

∑

4n + 7

100n −1

n=1

n=1

24. ∑ n

∞

n=1 1000n +1

27. ∑∞ n + 2

n=1 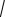n3

30. ∑∞ n +1 n2 n=1 n

20