groups_lections (Множества и группы)

Введение

ОТОБРАЖЕНИЯ И ПРЕОБРАЗОВАНИЯ МНОЖЕСТВ

§ 1. ОБЩЕЕ ОПРЕДЕЛЕНИЕ И ЧАСТНЫЕ ТИПЫ ОТОБРАЖЕНИЙ МНОЖЕСТВ.

Оп ределение 0. 1. Если каждому элементу х множества Х поставлен в соответствие один и только один элемент y множества Y, то говорят, что задано (определено) отображение множества X во ( в) множество Y и записывают кратко

f : X Y .

( 0. 1 )

Желая указать конкретные элементы множеств, связанные соотношением (0.1), применяют запись

y = f (x) ,

( 0. 2 )

и называют элемент y образом элемента х, а элемент х — прообразом элемента y при отображении f .

Замечание 1. В определении 0.1 предлог во (или в) несёт важную смысловую нагрузку, указывая на отличие отображения наиболее общего типа (отображения во ) от частного типа отображений (отображений на ).

В определении 0.1 отображения существенны два усло-

вия:

1)образ есть у каждого элемента множества Х;

2)отображаемый элемент может иметь только один образ. Без выполнения обоих этих условий нельзя говорить об отображении. Все другие обстоятельства несущественны для общего определения отображения, но могут характеризовать те или иные его особенности.

Определение 0.1 не требует, чтобы каждый элемент множества Y был образом какого-либо элемента множества Х.

Иначе говоря, допустимо, чтобы какие-нибудь элементы множества Y не имели прообразов в множестве Х. Но если у каждого элемента y множества Y найдётся хотя бы один прообраз в множестве Х, то это будет частным случаем отображения, который называют сюръекцией, или отображением на.

Определение 0. 2. Если каждому элементу х множества Х поставлен в соответствие один и только один образ в множестве Y так, что у каждого элемента y из Y имеется хотя бы один прообраз в множестве Х, то говорят, что задано отображение множества X на множество Y. Отображение на называют также сюръективным, или сюръекцией.

Поскольку сюръекция является частным случаем отображения в, к ней применимы обозначения (0.1) и (0.2), но особенно выразительным, подчёркивающим особенность ото-

бражения на , будет обозначение
f (X) = Y	( 0. 3 )

— всё множество Y является образом всего множества Х, или

областью значений отображения f. Всякое отображение на

является вместе с тем отображением в, но не всякое отображение в будет отображением на. В общем случае, когда отображение (0.1) не является сюръективным, из множества Y можно выделить подмножество Y1 Y, являющееся областью значений отображения f, и записать

f (X) = Y1 .

( 0. 3 )

Наиболее общее определение 0.1 не требует, чтобы образы различных элементов множества Х были различными. Если различные элементы множества Х будут иметь один и тот же образ в множестве Y, то это не нарушит требования однозначности отображения (0.1). Но если потребовать, чтобы любым различным элементам множества Х соответствовали различные образы, то получим частный случай отображения (0.1), называемый инъекцией (инъективным отображением).

форумстудентов.рф2

Определение 0. 3. Если каждому элементу х множества Х поставлен в соответствие один и только один образ в множестве Y так, что любым различным прообразам соответствуют различные образы, то говорят, что задано

инъективное отображение.

Инъективным может быть как отображение в, так и отображение на. Второй из этих случаев, т.е. инъективная сюръекция, представляет особенный интерес и будет рассмотрен ниже.

Следующая простая схема иллюстрирует различные частные случаи, которые могут встретиться при построении отображения f : X Y.

x1 y1	x4		x7 y5		y7
x2 y2	x5	y4	x8	y6	y8	( 0. 4 )
x3 y3	x6		x9
Здесь	Х = { x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 } ,
	Y = { y1 , y2 , y3 , y4 , y5 , y6 , y7 , y8 } ,

элементы y7 , y8 Y не имеют прообразов в множестве Х, элементы x4 , x5 , x6 отображаются в один и тот же элемент y4 без нарушения однозначности отображения, так как каждый из них имеет только один образ, элементы x8 , x9 отображаются в элемент y6 .

Выделив из множества Y подмножество

Y1 = { y1 , y2 , y3 , y4 , y5 , y6 },

построим на основании соответствий (0.4) сюръективное ото-

бражение f ( X ) = Y1 .

Выделив из множества Х подмножество

Х1 = { х1 , х2 , х3 , х7 },

построим на основании соответствий (0.4) инъективное отображение f1 : X1 Y множества X1 во множество Y.

Выделив из множества Y подмножество

Y2 = { y1 , y2 , y3 , y5 },

построим на основании соответствий (0.4) инъективное отображение

f 2 ( X1 ) = Y2

( 0. 5 )

множества X1 на множествоY2, т.е. инъективнуюсюръекцию. Замечательная особенность отображения (0.5), являющегося одновременно сюръективным и инъективным, заключается в том, что в нём участвует каждый элемент yk множества образов Y2 и у каждого yk имеется один и только один прообраз в X1. Совместное выполнение обоих этих требований означает, что наряду с отображением (0.5) определено обратное ему отображение (в обратном направлении: из Y2 на

X1)
f 2 1 ( Y2 ) = X1 ,	( 0. 5 )

тоже сюръективное и инъективное. Чтобы подчеркнуть такую двусторонность отображения, инъективную сюръекцию на-

зываютбиекцией, иливзаимнооднозначнымотображением.

Определение 0. 4. Если каждому элементу х множества Х поставлен в соответствие один и только один элемент в множестве Y так, что у каждого элемента y из Y

имеется один и только один прообраз в множестве Х, то гово-

рят, что задано взаимно однозначное соответствие между

множествами Х и Y и применяют запись
X Y .	( 0. 6 )

Замечание 2. Взаимно однозначное соответствие (0.6) между множествами Х и Y равносильно заданию двух отображений на:

f (X) = Y и f –1 (Y) = X , ( 0. 6 )

каждое из которых является взаимно однозначным, или обратимым (имеющим обратное). Можно сформулировать определение 0.4 взаимно однозначного отображения иначе:

Определение 0. 4 . Отображение f ( X ) = Y

множества X на множество Y называется взаимно однознач-

3 форумстудентов.рф4

ным, если любым различным элементам xi , x k множества X соответствуют различные же элементы yi = f (xi ), yk = f (xk ) в множестве Y.

Можно отображать множество Х не только в ( на) другое множество, но и в ( на) самого себя, т.е. ставить в соответствие каждому элементу х из множества Х определённый (в общем случае — другой) элемент того же множества Х.

Определение 0. 5. Отображение

f : X Х

( 0. 7 )

множества Х в себя называется преобразованием этого множества.

При преобразовании множества Х каждый его элемент имеет образ, также принадлежащий множеству Х, однако это не гарантирует, что образы всех элементов заполнят всё множество Х. Может быть так, что образы некоторых элементов совпадут друг с другом, т.е. хотя бы один из элементов множества Х будет иметь больше чем один прообраз, и потому могут быть в X элементы, которые не имеют ни одного прообраза в множестве Х. При таком преобразовании множество Х отображается в какое-нибудь из своих подмножеств, не совпадающих с множеством Х.

Преобразование множества Х может быть взаимно однозначным отображением множества Х на себя, т.е. биекцией. Взаимная однозначность преобразования будет обеспече-

на, если выполнено требование его сюръективности
f (X) = Х ,	( 0. 8 )
т.е. каждый элемент множества Х имеет прообраз в Х.

Определение 0. 6. Взаимно однозначное преобразование конечного множества называется подстанов-

кой.

Подстановку принято записывать в виде двухстрочной таблицы, в верхней строке которой перечисляются все элеме-

нты преобразуемого множества, а в нижней под каждым элементом множества записывается его образ при данном преобразовании. В качестве примера выпишем все подстановки множества, состоящего из трёх элементов А, В, С :

	ABC	ABC	ABC	ABC		ABC	ABC
	ABC	, B C A	, C AB ,	B A C ,		AC B ,	C B A	. ( 0. 9 )
		§ 2. ПРОИЗВЕДЕНИЕ ОТОБРАЖЕНИЙ.
	Рассмотрим отображения
		f : X Y ,		:		Y Z .		( 0. 10 )
В отображении			участвует каждый элемент y Y, а в отоб-
ражении		f могут участвовать не все элементы множества Y.

Но те элементы y Y, для которых определён прообраз в Х, т.е. элементы, представимые в виде

y = f (x) ,
участвуют последовательно в обоих отображениях:
z = ( y) = [ f (x) ] .	( 0. 10 )

Запись (0.10 ) имеет тот же смысл, что и запись (0.10) — по-

следовательное выполнение отображений f и ,	результатом
чего является отображение Ф множества Х во множество Z
Ф : X Z .	( 0. 10 )
Чтобы подчеркнуть, что отображение Ф заключается в
последовательном выполнении отображений f	и , пред-

ставляют оператор Ф в виде произведения операторов f		и :
Ф = f .	( 0.	10 )

При этом важно принять соглашение о порядке записи операторов, обозначающих последовательно выполняемые отображения. В математической литературе общепринято операцию, выполняемую в первую очередь, записывать справа от операции, выполняемой во вторую очередь. Например, запись

z = sin lg x означает, что от аргумента х берётся десятичный логарифм lg x = y, а затем это значение логарифма выступает

5 форумстудентов.рф6

в роли аргумента синуса. Пользуясь обозначением (0.10 ) последовательного выполнения отображений, сформулируем определение произведения отображений.

Определение 0. 7. Результат последовательного выполнения отображений f и называется их произведением f , если для каждого элемента х множества Х выполняется равенство

( f ) х = [ f (x)] .

( 0. 11 )

По смыслу определения 0.7 произведение отображений в общем случае не коммутативно, т.е. перемножаемые отображения нельзя менять местами. Действительно, если отображения (0.10) выполняются в порядке f (отображение f делается в первую очередь), то из них выстраивается цепочка соответствий между тремя множествами X Y Z, равносильная сложному отображению множества Х в множество Z, а выполнение отображений (0.10) в ином порядке Y Z, X Y не порождает сложного отображения и символ f не имеет смысла.

В тех случаях, когда речь идёт о взаимно однозначных преобразованиях одного и того же множества, например

f (X) = Х , (X) = Х ,

не будет лишено смысла изменение очерёдности преобразований, но и в таких случаях не гарантировано равенство про-

изведений f и	f . Для примера возьмём произведение двух
подстановок из (0.9):
ABC ABC	ABC		ABC	ABC		ABC
AC B C B A	= B C A	, но	C B A	AC B	=	C A B .
						( 0. 12 )

В соответствии с указанным выше общепринятым соглашением в первую очередь выполняется подстановка, записанная в виде правого сомножителя. Так, первое произведение под-

становок вычисляется как результат следующих цепочек отображений элементов:

A C B, B B C, C A A.

Особый интерес представляет произведение взаимно обратных отображений. Только взаимно однозначное отображение может иметь обратное отображение (см. замечание 2 между определениями 0.4 и 0.4 ). Применяя к каждому элементу х множества Х сначала отображение f ( x ) = y, а затем обратное отображение f –1 ( y ) = x , получим в соответствии с равенством (0.11) :

f –1 [ f (x)] = f –1 (y) = x = ( f –1 f ) x .

( 0. 13 )

Действие отображения f –1 f на каждый элемент х множества Х состоит, согласно последнему равенству в цепочке (0.13), в том, что этот элемент остаётся неизменным. Такое отображе-

ние называется тождественным и обозначается символом IˆX (первой буквой латинского слова idem — тот же) :

IˆX х = х ,	х Х.	( 0. 14 )
Значит произведение отображений
f –1 f =	IˆX	( 0. 15)

является тождественным отображением множества Х на себя, но назвать его преобразованием множества Х будет не вполне точным, поскольку в произведении участвует взаимно однозначное отображение f множества Х на другое множество Y.

Изменив последовательность отображений в произведении (0.15), получим тоже тождественное отображение, но

иного смысла:
f [ f –1 (y)] = f (x) = y = ( f f –1 ) y.	( 0. 16 )
Здесь произведение отображений
f f –1 = IˆY	( 0. 17 )

является тождественным отображением множества Y на себя. Различие смысла произведений отображений (0.15) и (0.17)

подчёркнуто индексами при символе Iˆ тождественного отображения. Различие произведений (0.15) и (0.17) полностью

7 форумстудентов.рф8

сотрётся, если f будет взаимно однозначным преобразованием множества Х (отображением множества на самого себя). Тогда отображение f не будет выводить элементы х за пределы множества Х и каждое из произведений (0.15) и (0.17) бу-

дет иметь смысл тождественного преобразования множест-

ва Х:

f f –1 = f –1 f = Iˆ .

( 0. 18 )

Отмеченная в двойном равенстве (0.18) коммутативность

прямого и обратного отображений (отсутствующая в отображениях (0.15) и (0.17)), является важным условием определения взаимно обратного преобразования множества. Именно это требование коммутативности произведения заложено в определение взаимно обратных матриц: AA–1= A–1A = E.

Определение 0. 8. Если f — взаимно однозначное преобразование множества Х, то выполнение двойного равенства (0.18) служит необходимым и достаточным признаком преобразования f –1, обратного преобразованию f.

Если речь идёт о подстановках (преобразованиях конечных множеств), то для получения обратной подстановки достаточно поменять местами строки в таблице подстановки. Так, в примере с произведениями подстановок (см. (0.12)) подстановка, обратная первому произведению

ABC		B C A
B C A	имеет вид	A BC .

Но в таком виде её трудно отождествить с одной из подстановок полного перечня (0.9), поскольку в том перечне элементы верхней строки всюду расположены в алфавитном порядке. Пользуясь тем, что содержание подстановки не изменится, если поменять местами столбики таблицы подстановки (в каждом столбике жёстко связаны прообраз и образ), представим найденную выше обратную подстановку в виде

ABC

C A B ,

в котором легко узнаётся второе из произведений (0.12). Произведения (0.12) подстановок удовлетворяют двойному равенству (0.18)

ABC	ABC	=		ABC	=	ABC	ABC	,
B C A	C A B			AB C		C A B	B C A

т.е. их последовательное выполнение в любом порядке даёт тождественную подстановку (первую в перечне (0.9)), как и следует взаимно обратным преобразованиям множества.

§ 3. АССОЦИАТИВНОСТЬ ПРОИЗВЕДЕНИЯ ОТОБРАЖЕНИЙ.

Из трёх последовательных отображений множеств

f : X Y ,	: Y Z ,	: Z U ,	( 0. 19 )
или в поэлементной записи
f (x) = y ,	(y) = z ,	(z) = u ,	( 0. 19 )

можно составить произведение отображений двумя способами, по-разному объединяя скобками соседние операторы:

( f )	и ( ) f .
Теорема 0. 1 .	Произведение отображений ас-

социативно, т.е. для любых трёх последовательно выполняемых отображений (0.19) справедливо равенство

( f ) = ( ) f .

( 0. 20 )

Пользуясь равенством (0.11), определяющим произведение отображений, легко получим следующие цепочки равенств, справедливые для любых элементов х Х:

u = (z) = [ ( y)] = { [ f (x)]} = [( f ) x] = [ ( f )] x, u = (z) = [ ( y)] = ( ) y = ( ) [ f (x)] = [( ) f ] x .

Так как левые части этих цепочек равенств одинаковы, то одинаковы и их правые части

[ ( f )] x = [ ( ) f ] x .

Выполнение этого равенства для любых элементов х Х означает, по определению 0.7, справедливость равенства (0.20).

9 форумстудентов.рф10

Определение 1.2.

Глава 1. ОПРЕДЕЛЕНИЕ И ОБЩИЕ СВОЙСТВА

ГРУПП

§ 1. ОПРЕДЕЛЕНИЕ БИНАРНОЙ АЛГЕБРАИЧЕСКОЙ ОПЕРАЦИИ НА МНОЖЕСТВЕ.

Определение 1.1. Если существует правило, по которому каждой упорядоченной паре элементов (a, b) множества M ставится в соответствие один и только один элемент d того же множества M, то говорят, что на этом мно-

жестве задана бинарная алгебраическая операция.

В дальнейшем мы будем говорить просто об алгебраической операции, подразумевая по умолчанию, что эта операция является бинарной, т.е. имеет два операнда (два элемента, которым ставится в соответствие результат операции). Если алгебраическая операция имеет смысл сложения, то её обозначают знаком плюс (+), а результат операции называют суммой. Если операция имеет смысл умножения, то её обозначают точкой или отсутствием таковой (a b или a b ), а результат операции называют произведением. Если же желательно говорить об операции в обобщённом смысле, не уточняя её содержание, то применяют значок ( ) или (○), а результат

обобщённой операции будем называть композицией
a * b = d .	( 1. 1 )

В определении 1.1 алгебраической операции на множестве M существенны четыре требования:

1) алгебраическую операцию можно применять к каждой (любой) паре элементов, в том числе и к одинаковым

элементам: a * a, b * b, … ;

2) результат операции над любыми элементами множества M есть элемент того же множества;

3)результат операции однозначен (один и только один элемент соответствует упорядоченной паре элементов);

4)упорядоченность пары элементов, участвующих в операции, оговорена в определении 1.1 ради его общности, но может оказаться и несущественной, если операция обладает

свойством коммутативности (a* b = b* a для любых элементов a и b).

§ 2. ОПРЕДЕЛЕНИЕ ГРУПП.

Группой называется множество G элементов любой природы, если на этом множестве определена бинарная алгебраическая операция и выполня-

ются следующие три требования:

1*. Операция ассоциативна, т.е. для любых элементов a, b, c множества G справедливо равенство

(a* b) * c = a * (b* c) .

( 1. 2 )

2*. В множестве G имеется нейтральный элемент ,

композиция которого с любым элементом a G удовлетворяет равенству

a* = a .	( 1. 3 )
3*. В множестве G для любого элемента a найдётся об-
ратный ему элемент a –1, удовлетворяющий равенству
a* a –1 = .	( 1. 4 )

Соотношения (1.2), (1.3), (1.4) называются аксиомами группы.

В общее определение группы не включено требование

коммутативности операции, но если такое требование a* b = b* a

выполняется для любых элементов a, b G, то группа назы-

вается коммутативной или абелевой.

Если группа состоит из конечного числа n элементов, то это число называют порядком группы и указывают в виде нижнего индекса при символе группы: Gn .

11форумстудентов.рф12

Если определённая на группе операция является сложением, то группу называют аддитивной (от латинского addo

— прибавлять, английского add с тем же значением). Если же определённая на группе операция является умножением, то группа называется мультипликативной (от латинского multiplico — умножать).

Подчеркнём следующее очень важное для дальнейшего обстоятельство. Когда потребуется выяснять, является ли некоторое множество группой, то нужно проверять выполнение четырёх требований: требование 0* — определённость на данном множестве бинарной алгебраической операции, и выполнение аксиом 1*, 2*, 3* группы.

§3. ПРИМЕРЫ ГРУПП.

I. Любое линейное пространство является группой по отношению к операции сложения элементов линейного пространства. Проверяем это утверждение по четырём пунктам.

0*. На любом линейном пространстве определена бинарная операция сложения его элементов (векторов).

1*. Эта операция ассоциативна:

(a + b) + c = a + (b + c) .

2*. Роль нейтрального по отношению к сложению элементов в линейном пространстве играет нулевой элемент o:

a + o = a .

3*. Роль обратного элемента для каждого элемента a линейного пространства играет противоположный ему элемент

(– a):

a + (– a) = o .

Таким образом всякое линейное пространство есть аддитивная группа (и притом коммутативная, по свойству операции сложения).

II. Множество R всех вещественных чисел является линейным пространством (одномерным) и, следовательно, группой по сложению (аддитивной). Хотя на множестве R определена и операция умножения его элементов, это множество не удовлетворяет третьей аксиоме группы по отношению к умножению, так как нейтральным элементом по отношению к операции умножения является число 1, и для числа 0 не существует обратного элемента 1/0 в R.

III. Множество R \ 0, получаемое исключением нулевого элемента из множества R всех вещественных чисел, уже не будет линейным пространством (из-за отсутствия нулевого элемента), но оно оказывается группой по отношению к операции умножения, т.е. мультипликативной группой с нейтральным элементом 1.

IV. Множество всех матриц одинаковых размеров

(n p) является линейным пространством, и следовательно, аддитивной группой. Нейтральный элемент этой группы — нулевая матрица размеров (n p).

V. Множество всех невырожденных матриц порядка n (т.е. квадратных матриц с отличным от нуля определителем) не является линейным пространством (из-за отсутствия в нём нулевой матрицы). Но это множество является группой относительно операции перемножения матриц, так как произведение невырожденных матриц порядка n принадлежит этому же множеству и выполнены все три аксиомы группы:

(АВ) С = А(ВС) — ассоциативность произведения, АЕ = А — существование единичной матрицы Е,

AA–1= A–1A = E — существование обратной матрицы А– 1 для каждой невырожденной матрицы А.

Более сложным примером, играющим важную роль в геометрических и физических приложениях, являются группы точечных преобразований симметрии геометрических фигур. Им нужно посвятить отдельный параграф.

13форумстудентов.рф14

§ 4. ТОЧЕЧНЫЕ ПРЕОБРАЗОВАНИЯ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР.

Оп ределение 1. 3. Геометрической фигурой называется множество точек пространства.

Мы будем иметь дело с наиболее важными для приложений фигурами в трёхмерном собственно евклидовом пространстве, в частности, на плоскости. Поэтому геометрические фигуры будут представлять любые комбинации точек, прямых или кривых линий (или участков линий), плоскостей или искривлённых поверхностей (или их участков); фигура может быть также конечным телом или совокупностью тел, расположенных как угодно.

Оп ределение 1. 4. Преобразованием сим-

метрии геометрической фигуры называется такое отображение фигуры самой на себя, при котором равные части фигуры отображаются друг на друга, а фигура в целом не изменяет своей формы и ориентации в пространстве. Иными словами, форма и ориентация фигуры после выполнения операции симметрии неотличимы от её формы и ориентации до выполнения операции.

Определение 1.5. Преобразование симметрии называется точечным, если при выполнении его хотя бы одна точка преобразуемой геометрической фигуры не изменяет своего положения в пространстве.

Бывают и не точечные преобразования симметрии, называемые пространственными. Например, сдвиг кристаллической решётки, при котором каждая ячейка решётки займёт положение одной из близких к ней ячеек, решётка в целом будет выглядеть так же, как и до сдвига (трансляции). Но в предлагаемом пособии речь будет идти только о точечных преобразованиях симметрии.

Определение 1.6. Элемент симметрии —

это точка, прямая или плоскость, обладающие тем свойством, что все точки элемента симметрии остаются неподвижными при выполнении соответствующего точечного преобразования симметрии фигуры.

Поскольку точечные преобразования симметрии должны сохранять неизменным положение хотя бы одной точки фигуры, это означает, что все оси и плоскости симметрии фигуры должны пересекаться в такой точке.

Композиция преобразований симметрии геометрической фигуры заключается в их последовательном выполнении, а так как последовательное выполнение преобразований любых множеств принято называть произведением преобразований, то и композицию преобразований симметрии называют их произведением, а группы преобразований симметрии фигур считают мультипликативными группами.

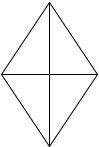
Рассмотрим в качестве простейшего начального примера преобразования симметрии ромба. Легко заметить в этой фигуре два элемента симметрии: диа-

Bгонали AC и BD. При выполнении операций отражения относительно этих диагоналей изменяют положение бес-

				конечно много точек ромба, но есть
C	O	A		очевидная возможность не рассматри-
				вать отражения бесконечного множест-
				ва точек, а рассмотреть только отраже-
				ния вершин ромба. Запишем в виде
	D			подстановок		вершин преобразования
				симметрии	(отражения) относительно
	Рис. 1.1
				этих диагоналей и тождественное пре-
образование ε:
	a = ABCD		,	b = ABCD	,	ε = ABCD	.	( 1. 5 )
	ADCB			CBAD		ABCD

15форумстудентов.рф16

Чтобы выяснить, является ли множество преобразований сим-

ции (они перечислены после формулы (1.1)) выполнены. Од-

метрии (1.5) группой, нужно выполнить проверку всех четы-

нозначность всех произведений в таблице (1.6) обеспечена са-

рёх условий в определении группы. Начинаем с условия 0*

мим смыслом рассматриваемых преобразований симметрии.

определённости бинарной операции. Одно из его требований

Трудней всего было бы доказывать, что правила пере-

заключается в том, чтобы композиция (в данном случае —

множения, записанные в таблице (1.6), удовлетворяют требо-

произведение преобразований симметрии) любых преобразо-

ванию аксиомы 1* ассоциативности. Трудность была бы вы-

ваний (1.5) принадлежало этому же множеству преобразова-

звана необходимостью рассматривать большое количество

ний (1.5). Начнём с произведения ab:

произведений вида (ab) c, a (bc), b (ac), (ba) c, … и т.д. Но от

ABCD

ABCD

ABCD

с .

такой необходимости нас избавляет теорема 0.1 в §3, которой

ab = ADCB

CBAD =

CDAB

=

( 1. 5 )

доказано с полной общностью, что произведение любых ото-

Так как этого элемента ab = c нет в множестве преобразова-

бражений (а значит и преобразований) ассоциативно.

Выполнение аксиом 2* и 3* усматривается ясно в таб-

ний (1.5), то множество (1.5) не является группой. Присоеди-

лице (1.6). Первый столбец показывает, что каждый элемент

нив преобразование (1.5 ) к

множеству

(1.5), надо будет проверять, является ли

ε

a

b

c

группы остаётся неизменным при умножении его на нейтра-

ε

ε

a

b

c

льный элемент ε (аксиома 2*). В каждой из строк таблицы, по-

группой расширенное множество преоб-

разований ε, a, b, c. Чтобы придать таким

a

a

ε

c

b

меченных в заглавном столбце обозначением ai одного из

проверкам систематический

характер,

b

b

c

ε

a

элементов группы, присутствует нейтральный элемент, указы-

удобно пользоваться таблицами типа ту-

вая, какой элемент ak заглавной строки является обратным для

c

c

b

a

ε

элемента ai (аксиома 3*). Итак, существование таблицы (1.6)

рнирных, в которых заносится в опреде-

( 1. 6 )

умножения четырёх преобразований симметрии ромба дока-

лённую клетку таблицы результат встре-

зывает, что эти преобразования образуют группу 4-го поряд-

чи любых игроков. Разница лишь в том, что в турнирах ника-

ка. Таблицы такого типа, составленные для различных конеч-

кой игрок не играет сам с собой, а в таблице произведения

ных групп, называются таблицами Кэли в честь английского

преобразований любое преобразование может умножаться и

математика Артура Кэли (Cayley).

на самого себя. Пользуясь методом перемножения подстано-

вок или иными наглядными соображениями построим табли-

Всё разнообразие точечных преобразований симмет-

цу (1.6). Вэтой таблице есть заглавная строка и заглавный сто-

лбец. В заглавной строке будем записывать правый сомножи-

рии геометрических фигур в трёхмерном собственно евклидо-

тель произведения элементов группы, а в заглавном столбце

вом пространстве (так классифицируется наблюдаемое прост-

— левый сомножитель. Так как на пересечении строки a таб-

ранство, знакомое всем по чувственным восприятиям и шко-

лицы и столбца b находится элемент ab = с. Таблица (1.6) яс-

льному курсу геометрии) разбивается на три типа: 1) поворо-

но показывает, что среди всех возможных попарных произве-

ты вокруг осей, 2) отражения относительно плоскостей сим-

дений элементов из множества ε, a, b, c нет ни одного элемен-

метрии и так называемые 3) зеркальные повороты. Познако-

та, не принадлежащего этому множеству. Тем самым доказа-

мимся с ними на примере треугольного диэдра.

но, что требования 1) и 2) из определения 1.1 бинарной опера-

17форумстудентов.рф18

Рис. 1.2

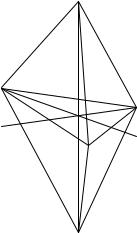
Определение 1.7. Диэдром называется правильная удвоенная пирамида (бипирамида), состоящая из двуходинаковых правильных пирамид, сложенныхсвоими основаниями.

У треугольного диэдра таким общим основанием является правильный треугольник (см. рис. 1.2). Биссектрисы, они же медианы и высóты правильного треугольника основания

	P			ABC являются		поворотными
				осями	второго порядка. Пово-
				ротами	вокруг	оси		симметрии
				фигура может быть совмещена
				сама с собой. Если min — вы-
B				раженный в градусах наимень-
				ший из всех углов поворота во-
O			A
		b		круг оси, приводящий к самосо-
a
				вмещению фигуры, то число
	C
					n =	360	о	( 1. 7 )
						min

называется порядком оси. Поворотную ось порядка n обоз- Q начают символом Cn . Показанная на рис. 1.2 ось ОА, совпадающая с биссектрисой угла ВАС,

является осью C2 . Операцию поворота диэдра вокруг оси OA на угол 180о мы обозначим буквой a. Так как форма и положение треугольного диэдра определяются положением пяти его вершин, то любое преобразование симметрии этой фигуры можно задать в виде подстановки множества шести элементов. Выпишем подстановки a, b, c, выражающие повороты второго порядка вокруг осей ОА, ОВ, ОС соответственно:

	A B C P Q	,		A B C P Q	,		A B C P Q	. ( 1. 8 )
a =			b =			c =
	AC B Q P		C B AQ P			B AC Q P

Поворотной осью симметрии всякого диэдра является прямая, соединяющая вершины обеих его пирамид. На рис.1.2 это прямая PQ — ось С3 третьего порядка. Операцию поворота на минимальный угол (в данном случае min = 120 о) обозначают тем же символом, что и саму поворотную ось. Но ради однообразия с обозначениями операций (1.8) мы обозначим эту операцию буквой d (d=С3). Операция поворота на два минимальных угла представляет собой произведение операций поворота на один минимальный угол, т. е. вторую степень

операции d : d 2 =C32 . Операция d3 = C33 поворота на три мини-

мальных угла (3 min = 3 120 о = 360 о) возвращает все точки треугольного диэдра в их исходное положение, т.е. совпадает

с тождественным преобразованием этой фигуры (d 3 = C33 = ε).

Выпишем подстановки множества вершин треугольного диэдра, соответствующие трём поворотам вокруг оси С3:

	A B C P Q	, d2		A B C P Q		A B C P Q	. ( 1. 9 )
d =			=		, =
B C A P Q			C A B P Q			A B C P Q

Если геометрическая фигура имеет поворотные оси различных порядков, то ось наибольшего порядка называется главной осью симметрии. У диэдра главной осью является ось, проходящая через вершины обеих его пирамид.

Диэдр имеет плоскости симметрии AOP, BOP, COP,

ABC. Плоскость симметрии и операция отражения геометрической фигуры относительно плоскости симметрии обозначается буквой . Любая плоскость симметрии порождает только две различных операции симметрии: операцию и квадрат этой операции, совпадающий с тождественным преобразова-

нием фигуры
2 = I = .	( 1. 10 )

Выпишем подстановки множества вершин треугольного диэдра, соответствующие отражениям в его плоскостях симметрии:

19форумстудентов.рф20