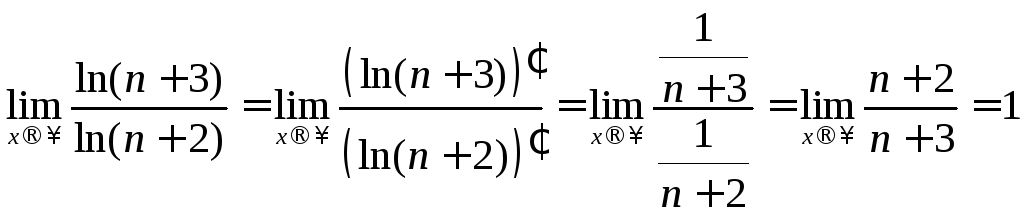МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

Московский государственный университет тонких химических технологий им. М.В.Ломоносова

Кафедра высшей и прикладной математики

Л.М. Ожерелкова, А.Г. Рубин, И.А. Джемесюк

Введение в теорию рядов

Учебно-методическое пособие

Москва 2012

УДК 51

ББК 22.1

Рецензент – доктор физ.-мат.наук, профессор Карташов Э.М.

Л.М. Ожерелкова, А.Г. Рубин, И.А. Джемесюк

Введение в теорию рядов. Учебно-методическое пособие. М.:ИПЦ МИТХТ, 44 с.

Утверждено библиотечно-издательской комиссией

в качестве учебно-методического пособия

для студентов 2–4-го курсов дневного отделения

всех специальностей МИТХТ им. М.В.Ломоносова

по дисциплине «Высшая математика», поз. /2011.

ÓМИТХТ им. М.В.Ломоносова, 2012

§1. Основные понятия

Определение.Числовым рядомназывается бесконечная последовательность чисел, соединенных знаком сложения:

. (1)

Числа называютсячленами ряда, а член–общим или n-м членом ряда.

Ряд (1) считается заданным, если известен его общий член , (), т.е. задана функциянатурального аргумента. Например, ряд с общим членомимеет вид:

Образуем новую последовательность:

………………..

Определение. Суммапервых членов ряда называетсяn-ой частичной суммой рядаи обозначается.

Определение.Если последовательность частичных сумм ряда имеет предел, то такой ряд называетсясходящимся, а этот предел называетсясуммой ряда.

То есть если , то ряд сходится, а– сумма ряда. В этом смысле можно записать.

Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся. У расходящегося ряда суммы нет.

Пример 1. Исследовать на сходимостьгеометрический ряд, т.е. ряд, составленный из последовательных членов геометрической прогрессии:

(2)

Решение:Необходимо установить, при каких значениях знаменателя прогрессииряд (2) сходится, а при каких – расходится. Из школьного курса алгебры известно, что сумма первыхчленов геометрической прогрессии, т.е.n-я частичная сумма ряда приравна.

Возможно несколько случаев:

1) если , тои

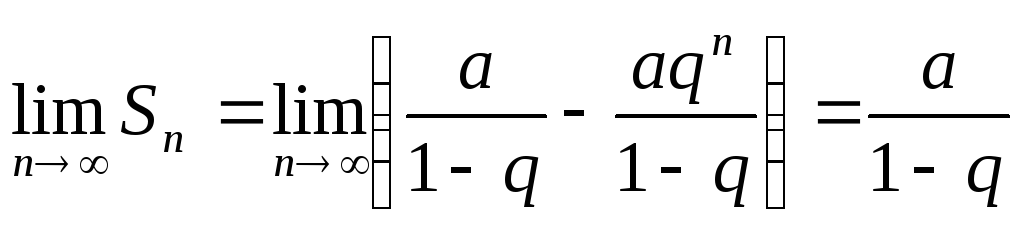, т.е. ряд сходится и его сумма.

2) если , тои, следовательно,и ряд расходится.

3) если , то ряд (2) примет вид, егои,ряд расходится.

4) если , то ряд (2) примет вид, и егопричетном ипринечетном, следовательно,не существует, и ряд расходится.

Т.о. геометрический ряд сходится к сумме прии расходится при.

Пример 2. Найти сумму ряда:

(3)

Решение: -я частичная сумма ряда:

Учитывая, что

,,,...,,

и тогда частичную сумму ряда можно представить в виде

получаем:, т.е. сумма ряда.

§2. Свойства сходящихся рядов

Свойство 1.Если рядсходится и имеет сумму, то и ряд, полученный умножением данного ряда на число, также сходится, и имеет сумму.

Свойство 2.Если рядыисходятся и их суммы соответственно равныи, то и рядытакже сходятся и их суммы равны соответственнои.

Свойство 3.Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или добавления) конечного числа членов.

Установить сходимость (расходимость) ряда путем нахождения частичной суммы и вычисления, как это сделано в примерах 1 и 2, возможно лишь в редчайших случаях из-за принципиальных трудностей при нахождении(суммировании первыхчленов ряда). Обычно сходимость (расходимость) ряда устанавливается с помощью специальных теорем –признаков сходимости.

В большинстве признаков сходимости вам придется вычислять некоторый предел. Напомним кратко два основных приема вычисления пределов, которыми вы будете пользоваться чаще всего.

А) Предел отношения двух степенных выражений на бесконечности равен:

0, если степень числителя меньше степени знаменателя;

, если степень числителя больше степени знаменателя;

отношению старших коэффициентов, если степень числителя равна степени знаменателя^*.

Б) Правило Лопиталя. Предел отношения двух бесконечно малых величин (б.м.) или двух бесконечно больших величин (б.б.) равен пределу отношения их производных. Например, по правилу Лопиталя имеем: