
1. Вычисление площадей плоских фигур.
Если
плоская фигура ограничена прямыми
![]() и
кривыми
и
кривыми![]() ,
причем,
,
причем,![]() ,
то её площадь вычисляется по формуле
,
то её площадь вычисляется по формуле
![]() .
.
В
отдельных случаях левая граница
![]() (или
правая граница
(или
правая граница![]() )
может выродиться в точку пересечения
кривых
)
может выродиться в точку пересечения
кривых![]() и
и![]() .
В этих случаях величины
.
В этих случаях величины![]() и
и![]() отыскиваются
как абсциссы точек пересечения указанных
кривых (см.рис.4.1.)
отыскиваются
как абсциссы точек пересечения указанных
кривых (см.рис.4.1.)

Если
граница фигуры задана параметрическими
уравнениями![]() ,
то площадь фигуры вычисляется по одной
из трёх формул:
,
то площадь фигуры вычисляется по одной
из трёх формул:
![]() ,
,
где
![]() и
и
![]() -
значения параметра
-
значения параметра![]() ,соответствующие
началу и концу обхода контура в
положительном направлении (при котором
фигура остается слева).
,соответствующие
началу и концу обхода контура в
положительном направлении (при котором
фигура остается слева).
В
полярных координатах площадь сектора,
ограниченного дугой кривой
![]() и
лучами
и
лучами![]() и
и![]() ,
выражается
формулой
,
выражается
формулой
![]() .
.
Пример.
Вычислить
площадь фигуры, ограниченной прямыми
![]() ,
,![]() и кривыми
и кривыми![]() ,
,![]() .
.
Решение.
Т ак
как максимум функции
ак
как максимум функции![]() достигается
в точке
достигается
в точке
![]() и равен 1, а функция
и равен 1, а функция![]() на отрезке
на отрезке![]() ,
то (см. рис. 4.2.)
,
то (см. рис. 4.2.)
![]()
![]() .
.
Пример.
Вычислить
площадь фигуры, ограниченной параболами
![]() ,
,![]() .
.
Р ешение.
ешение.
Решая систему уравнений
![]()
найдем
ординаты точек пересечения кривых![]() ,
,![]() .
.
Так
как
![]() при
при![]() ,то
,то
![]()
![]() .
.
Пример.
Вычислить площадь фигуры, ограниченной эллипсом
![]()
Решение.
Здесь удобно вычислить сначала
![]() .
.
Отсюда
![]()
 .
.
Пример.
Найти
площадь фигуры,
ограниченной
одним лепестком кривой
![]() (лемниската).
(лемниската).
Решение.
Правая
часть уравнения кривой неотрицательна
при значениях
![]() ,
для которых
,
для которых![]() .
.
Поэтому первый лепесток лежит в угловом секторе, в котором
![]() ,т.е.
,т.е.
![]() .
.
Следовательно,

![]() .
.
2. Вычисление длин дуг плоских кривых
Если
плоская кривая задана уравнением в
декартовых координатах
![]() и производная
и производная![]() непрерывна,
то длина дуги этой кривой вычисляется
по формуле
непрерывна,
то длина дуги этой кривой вычисляется
по формуле
![]() ,
,
где
![]() и
и![]() -абсциссы
концов данной дуги.
-абсциссы
концов данной дуги.
Если
кривая задана уравнениями в параметрической
форме![]() ,
,![]() и производные
и производные
![]() и
и![]() непрерывны
на отрезке
непрерывны
на отрезке![]() ,
то длина
дуги кривой выражается формулой
,
то длина
дуги кривой выражается формулой
 ,
,
где
![]() и
и![]() - значения параметра
- значения параметра![]() ,
соответствующие
концам дуги
,
соответствующие
концам дуги
![]() .
.
Если
кривая задана уравнением
![]() в
полярных координатах, то длина дуги
в
полярных координатах, то длина дуги![]() кривой выражается интегралом
кривой выражается интегралом
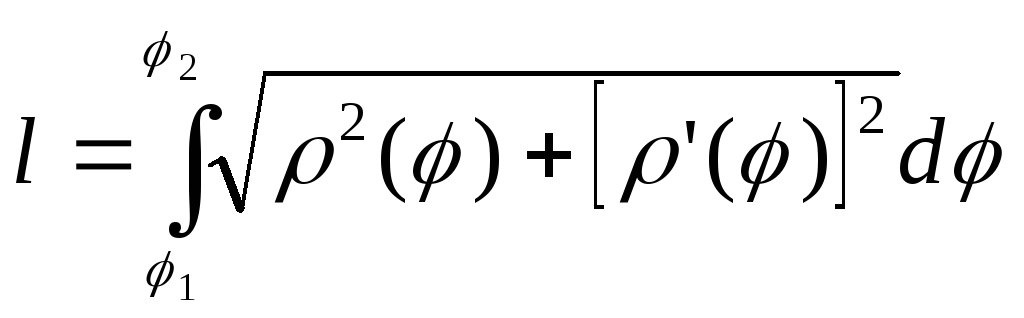 ,
,
где
![]() и
и![]() - значения полярного угла
- значения полярного угла![]() в
концах дуги
в
концах дуги![]() .
.
Пример.
Вычислить
длину дуги полукубической параболы
![]() ,
заключенной
между точками
,
заключенной
между точками
![]() и
и![]() .
.
Р ешение.
ешение.
Функция
![]() определена
при
определена
при![]() .
Поскольку данные точки
.
Поскольку данные точки![]() и
и
![]() лежат в первой четверти, то
лежат в первой четверти, то![]() .
.
Отсюда
![]() ,
,
![]() .
.
Следовательно,
![]() .
.
Пример.
Вычислить длину дуги развертки круга
![]() от
от![]() до
до![]() .
.
Решение.
Дифференцируя
по![]() ,
получим
,
получим
![]() ,
,
откуда
![]() .
.
Следовательно,
![]() .
.
Пример.
Найти
длину первого витка архимедовой спирали![]() .
.
Решение.
Первый
виток архимедовой спирали образуется
при изменении полярного угла от
![]() до
до![]() .
Поэтому
.
Поэтому
![]() .
.
Вычислим
первообразную для функции
![]() методом интегрирования по частям:
методом интегрирования по частям:

![]()
![]() .
.
Откуда
![]() ,
,
![]() ,
,
и, следовательно,
![]()
![]() .
.
3. Вычисление объемов тел
Объем тела выражается интегралом
![]() ,
,
где
![]() -
площадь сечения тела плоскостью,
перпендикулярной к оси
-
площадь сечения тела плоскостью,
перпендикулярной к оси![]() в точке с абсциссой
в точке с абсциссой![]() .
.![]() и
и![]() - левая и правая границы изменения
- левая и правая границы изменения![]() ,
,![]() непрерывна
при
непрерывна
при![]() .
.
Объем
тела, образованного вращением вокруг
оси
![]() криволинейной трапеции, ограниченной
кривой
криволинейной трапеции, ограниченной
кривой![]() ,
осью абсцисс и прямыми
,
осью абсцисс и прямыми![]() ,
,![]() ,
выражается
интегралом
,
выражается
интегралом
![]() .
.
Объем
тела, образованного вращением вокруг
оси
![]() фигуры,
ограниченной кривыми
фигуры,
ограниченной кривыми![]() и
и![]()
![]() и прямыми
и прямыми![]() и
и![]() ,
выражается формулой
,
выражается формулой
![]() .
.
Если кривая задана параметрически или в полярных координатах, то следует сделать соответствующую замену переменной в указанных формулах.
Пример.
Найти объем эллипсоида
![]() .
.
Р ешение.
ешение.
Сечение
эллипсоида плоскостью
![]() есть
эллипс
есть
эллипс
![]()

с
полуосями
![]() и
и![]() .
.
Следовательно площадь сечения
![]()
Поэтому объем эллипсоида
![]() .
.
Положив,
в частности,![]() ,получим
объем шара
,получим
объем шара
![]() .
.
Пример.
Вычислить вокруг оси абсцисс объем тела, которое образуется при вращении одной арки циклоиды
![]()
в округ
оси абсцисс.
округ
оси абсцисс.
![]()
делаем замену переменной, полагая
![]() .
.
|
|
|
|
0 |
0 |
|
|
|
![]()
![]()
![]()
![]()
![]()
![]() .
.
Контрольная работа №4 по теме
