3. Интегрирования по частям в неопределенном интеграле

При вычислении интегралов часто используется операция интегрирования по частям,законность которой регламентируется следующим утверждением.

Теорема 3. Пусть функции непрерывно дифференцируемы на множестве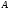Тогда на этом множестве справедливо равенство

Доказательство вытекает из цепочки тождеств

Замечание 2. Операция интегрирования по частям применяется к интегралам вида

(многочлен степени).

При этом в интегралах типа 1 для получения дифференциала надо ввести под знак дифференциала трансцендентную функциюа в интегралах типа 2 под знак диффере-

нциала надо ввести многочлен Например,

4.Выделение полного квадрата

При интегрировании алгебраических дробей будет использоваться операция выделения полного квадрата. Продемонстрируем ее на примере интеграла

5. Определенный интеграл, его свойства и геометрический смысл

Пусть функция определена на отрезкеПроизведем разбиение (см. Р5)

отрезка на частичные отрезкии выберем произвольно точкиВычислим значения

и составим так называемую интегральную сумму

Определение 3. Если существует конечный предел интегральных сумм:

и если этот предел не зависит от вида разбиения и выбора точекто его называютопределенным интегралом от функции на отрезке Обозначение:При этом саму функциюназываютинтегрируемой на отрезке

(заметим, что число называется диаметром разбиения ).

Пусть теперь функция По разбиениюстроится ступенчатая фигура (см. Р6), состоящая из прямоугольниковвысотыи длиной основания, равной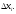Площадь этой ступенчатой фигуры (достройте ее самостоятельно) равна интегральной суммеи эта площадь будет приближенно равна площади криволинейной трапеции² т.е. 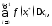причем это равенство будет тем точнее, чем меньше диаметр разбиенияи оно становится точным при

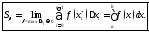
Мы пришли к следующему геометрическому смыслу определенного интеграла:

интегралчисленно равен площадикриволинейной трапециис верхней границей, описываемой уравнением

Замечание 3. В определении 3 интегралапредполагается, что отрезок интегрирования ориентирован отдо(т.е.). В случае противоположной ориентации отрезка

(т.е. при ) полагаем по определениюТакже полагаем по определению, что

Перейдем к формулировке свойств определенного интеграла.

Ограниченность подынтегральной функции. Если функция интегрируема на отрезкето она ограничена на этом отрезке (т.е.).

Линейность интеграла. Если функции иинтегрируемы на отрезкето на этом отрезке интегрируема и любая их линейная комбинация и имеет место равенство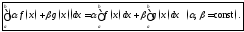

Аддитивность интеграла. Если функция интегрируема на максимальном из отрезков то она интегрируема и на двух других отрезках, причем имеет место равенство

Далее везде предполагаем, что

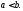
Монотонность интеграла. Если функции иинтегрируемы на отрезкеито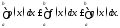

Интегрируемость модуля. Если функции 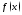интегрируема на отрезкето на этом отрезке интегрируема и функция 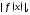причем имеет место неравенство

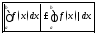
Теорема о среднем для интеграла. Пусть функция непрерывна на отрезкеТогда существует точка такая, что(геометрический смысл этой теоремы состоит в том, что существует прямоугольник с основаниеми высотыравновеликий криволинейной трапеции).

Доказательство. Пусть(по теореме Вейерштрасса значенияифункциейдостигаются). Имеемпоэтому из свойства монотонности интеграла отсюда получаем

Последние неравенства показывают, что значение является промежуточным для функции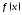на отрезкеа, значит, по теореме Больцано-Коши существуеттакое, что

Теорема доказана.

Рассмотрим ещё несколько примеров, которые демонстрируют простейшие приемы интегрирования.

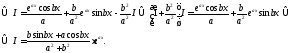
Лекция 6. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле. Интегрирование дробно-рациональных функций и тригонометрических выражений

Вычисление определенного интеграла можно свести к вычислению неопределенного. Соответствующая формула носит название формулы Ньютона-Лейбница. Для ее вывода необходимо изучить сначала свойства интеграла с переменным верхним пределом, к описанию которого мы переходим.