1. Интеграл с переменным верхним пределом

Заметим, что в качестве переменной интегрирования можно выбрать любую букву:

Пусть функция интегрируема на отрезкеТогда для любогоможно вычислить числоЗначит, для каждогоопределена функцияЭту функцию называютинтегралом с переменным верхним пределом.

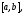Теорема 1. Если функция интегрируема на отрезкето интегралнепрерывен на этом отрезке. Еслинепрерывна на отрезкето

дифференцируема на указанном отрезке, причем

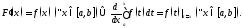
Доказательство первой части этого утверждения опускаем. Перейдем к обоснованию второй части. Пусть произвольная точка интервалаВычислим

Так как непрерывна на отрезкето применима теорема о среднем: существует точкатакая, что

Тогда Устремляя здесьи учитывая, что при этомт.е.Равенство (1) показано в любой внутренней точке отрезкаМожно показать, что оно верно и на концах этого отрезка. Теорема доказана.

Следствие 1. Любая непрерывная на отрезке функцияимеет первообразную.

Действительно, в качестве одной из первообразных можно указать интегралс переменным верхним пределом ().

2. Формула Ньютона-Лейбница

Докажем теперь одну из основных формул интегрального исчисления.

Теорема 2. Пусть функция непрерывна на отрезкеиеё первообразная на отрезкеТогда

Доказательство. Так как первообразная функциина отрезке, то существует постояннаятакая, чтоПоложим в этом равенствебудем иметьПоэтому

Полагая здесь получаем формулу (2). Теорема доказана.

Например,

3. Замена переменных и интегрирование по частям в определенном интеграле

С помощью формулы Ньютона-Лейбница нетрудно доказать следующие утверждения.

Теорема 3 (см. Р7). Пусть функция непрерывна на отрезке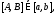а функциянепрерывно-дифференцируема на отрезке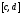таком, чтопричемТогда имеет место формула замены переменных в определенном интеграле:

Теорема 4. Пусть функции непрерывно-дифференцируемы на отрезкеТогда имеет место формула интегрирования по частям в определенном интеграле:

4. Интегрирование дробно-рациональных функций

Дробно-рациональной функцией (или алгебраической дробью) называется функция, представимая в виде отношения двух многочленов:

При этом дробь называетсяправильной, если степень ее многочлена-числителя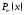меньше степениеё многочлена-знаменателяв противном случае (т.е. в случае) дробьназываетсянеправильной. Любую неправильную дробь можно представить в виде суммы многочлена (целой части) и правильной дроби. Для этого надо разделить числитель на знаменатель углом. Например,

Определение 1. Простейшими дробями типа называются следующие дроби:

где действительные постоянные,натуральные числа.

Теорема 5. Любую правильную дробь можно разложить в сумму простейших дробей типаЭто разложение единственно (с точностью до порядка слагаемых).

Алгоритм разложения на простейшие дроби

Пусть требуется разложить на простейшие дроби правильную дробь

Выполним следующие действия:

1) разложим знаменатель на множители:

2) каждому “линейному” множителю поставим в соответствие суммупростейших дробей типа

а каждому “квадратичному” множителю поставим в соответствиедробей типа

Сделав это для каждого множителя знаменателя запишем тождество

3) Умножив обе части этого тождества на знаменатель получим тождество двух многочленов. Приравнивая в нем коэффициенты при одинаковых степеняхполучим линейную алгебраическую систему уравнений относительно неопределенных коэффициентоврешая которую (например, методом Гаусса), найдем эти

коэффициенты. Подставляя их в (3), получим разложение дроби на простейшие дроби.

Например, разложим дробь на простейшие.

Так как то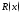представляется в виде

где коэффициенты пока не найдены. Приводя правую часть к общему знаменателю, а затем отбрасывая в обеих частях одинаковые знаменатели, получим тождество

Можно было бы приравнять здесь коэффициенты при одинаковых степенях (начиная с), а затем решить полученную систему уравнений относительноНо мы поступим проще. Применим так называемыйметод частных значений.

Так как (5) – тождество, то оно верно при любых значениях Удобно выбрать значениеПри этом из (5) получаем равенствооткуда выводим, чтоДалее подставляемв (4) и переносим все первые слагаемые влево; будем иметь

Разделив обе части этого тождества на 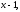получим

Полагая здесь снова будем иметьи последнее равенство перепишется в видеОтсюда сразу же находимСледовательно, все коэффициенты разложения (4) найдены и мы получаем

ответ:

Из теоремы 5 вытекает, что интегрирование правильных алгебраических дробей сводится к их разложению на простейшие дроби и последующему интегрированию последних. Займемся задачей интегрирования простейших дробей.

Дроби типа интегрируются очевидным образом:

Дробь типа интегрируется следующим образом:

Дробь типа интегрируется сложнее. Сначала производятся все операции, применяемые при интегрировании дроби типаа затем используется рекуррентная формула

Например,

В заключение предлагаем вычислить самостоятельно интеграл

и получить ответ: