3. Выпуклость, вогнутость, точки перегиба

Пусть функция дифференцируема в точкеТогда в точкеона имеет касательную, каждая точка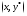которой удовлетворяет уравнению

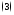
Определение 3. Говорят, что кривая выпукла вверх в точке если существует такое, что в окрестностикриваянаходится

ниже своей касательной (3) в точке т.е. еслиЕсли же

то криваяназываетсявыпуклой внизв точке (часто говорят, о выпуклости или вогнутости в точке ). Говорят, что криваявыпукла вверх (выпукла вниз) на интервале если она выпукла вверх (выпукла вниз) в каждой точкеэтого интервала.

На рисунке Р.2 функция выпукла вверх в точкеа на Р.3 – выпукла вниз.

Теорема 3. Пусть функция 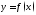дважды дифференцируема на интервале. Тогда справедливы высказывания:

1. если то кривая выпукла вверх на

2. если то кривая выпукла вниз на

Доказательство. Пусть произвольная точка интервала Окружим её отрезком Так как функцияудовлетворяет на этом отрезке всем условиям теоремы Тейлора с остаточным членом в форме Лагранжа, то для всехимеет место представление

С другой стороны, в точке 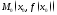функция имеет касательную с уравнением .Значит,Отсюда видно, что если(тогда и), тозначит,

кривая выпукла вверх в точке Если же то то значит,кривая выпукла вниз в точке Теорема доказана.

Определение 4. Точканазывается точкой перегиба кривой если:а)дифференцируема в точке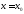; б) криваяпри переходечерез точкуизменяет направление выпуклости (это равносильно тому, что разностьизменяет знак при переходечерез точку).

Необходимое условие точки перегиба. Если - точка перегиба и если существутто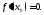

Доказательство вытекает из локальной формулы Тейлора и из равенства

Замечание 4. К точкам, подозрительным на “перегиб”, следует отнести, прежде всего, точки , для которыхОднако “перегиб” может иметь место и в точках, в которыхвторая производная не существует или равна Например, в точке функцияимеет производнуюИ в этой точке эта функция имеет “перегиб”. Очевиден следующий результат.

Теорема 4 (достаточное условие точки перегиба). Пусть функциядифференцируема в точкеи некоторой её окрестности и дважды дифференцируема в некоторой проколотой окрестности этой точки. Тогда если при переходечерез точкувторая производная изменяет знак, то точкаперегиба кривой

4. Исследование функций с помощью высших производных

Используя локальную формулу Тейлора, можно доказать следующие утверждения.

4. Пусть функция дифференцируема раз в критической точкеи пусть при этом

Тогда если то прив точкефункциядостигает минимума; прифункциядостигает максимума в точке.Если же

то в точке функцияне имеет локального экстремума.

_{5. Пусть функция} трижды дифференцируема в точке и выполнены условия: а)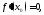б)Тогда–точка перегиба кривой

Например, при исследовании функции 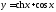на экстремум в точкеисследовать знак производнойдовольно сложно. Так как

то (согласно утверждению 4) в точкефункциядостигает минимума.

Лекция 5. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица первообразных. Простейшие приемы интегрирования: подведение функции под знак дифференциала, выделение полного квадрата, замена переменных и интегрирование по частям в неопределенном интеграле. Определенный интеграл, его свойства и геометрический смысл

Операция, обратная дифференцированию, называется интегрированием. Перейдем к ее изложению.