2. Локальный экстремум

Пусть функция определена в точкеи некоторой её окрестности.

Определение 2. Говорят, что функция достигает в точкелокального максимума, если существует такое, чтовыполняется неравенство. Если при указанныхимеет место противоположное неравенството говорят, что в точкефункциядостигает в точкелокального минимума.

Заметим, если неравенстваилиобращаются в равенстволишь в одной точке то говорят, что соответствующий максимум или минимум является строгим. Точки 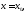функциядостигает локального максимума или минимума, называютсяточками локального экстремума этой функции.

Замечание 2. Слово “локальный” здесь означает, что введенное понятие экстремума верно лишь в достаточно малой окрестности точки 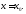Иногда слово “локальный” будем опускать.

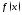Необходимое условие экстремума. Пусть в точке функция достигает локального экстремума. Тогда либо в этой точке функция дифференцируема и тогда 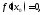либо не дифференцируема в точке

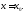
Замечание 3. Точки такие, чтолибо равна нулю, либо не существует (или равна), называтсякритическими точками функции

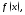Если точка локального экстремума функциито она обязательно для неё критическая. Обратное утверждение, вообще говоря, не верно. Например, для функциипроизводнаяно в точкеэта функция не имеет экстремума. Как проверить, что в критической точке достигается экстремум? Ответ на этот вопрос содержится в следующем утверждении.

Теорема 2 (достаточные условия экстремума по первой производной). Пусть точка критическая точка для функциии функция непрерывна в этой точке. Пусть, кроме того, производная существует в некоторой проколотой окрестности точки Тогда:

1. если при переходе аргумента через точку(слева направо) изменяет знак снато в точкефункциядостигает локального максимума;

2. если при переходе аргумента через точку(слева направо) изменяет знак снато в точкефункциядостигает локального минимума;

3. если в окрестности точки функцияне изменяет знака, то в точкефункцияне достигает локального экстремума.

Доказательство. Действительно, если то функциявозрастает на отрезкеи, значит,для всехиз указанного отрезка. С другой стороны, так както функцияубывает на отрезкеи, значит, сновадля всехиз указанного отрезка. Следовательно, при всехвыполняется неравенствот.е. точка является точкой локального максимума. Аналогично доказываются утверждения 2 и 3. Теорема доказана.

Например, рассмотренная выше функция имеет в точкеминимум, так какпри переходе через критическую точкуизменяет знак с минуса на плюс. Другие достаточные условия экстремума с помощью высших производных будут даны позже. А сейчас приведем схему построения графика функции

с помощью первой производной. Сделаем это для конкретной функции 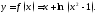Напомним сначала информацию о вычислении асимптот.

Если то прямаявертикальная асимптота для функции Если существуют конечные пределы

то прямая асимптота кривой Таким образом, асимптоты функции

могут возникнуть при подходе к точкам разрыва второго рода этой функции либо на бесконечности.

Схема построения графика функции с помощью первой производной.

1. Находим область определения функции

2. Находим (если это возможно) нули функции и ее интервалы знакопостоянства. Этот пункт мы опускаем, так как не можем точно решить уравнение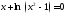(его приближенный корень равен 1.1478).

3. Находим точки разрыва функции и её асимптоты.

а) вертикальные асимптоты: так как

наклонных и горизонтальных асимптот нет, так как один из выписанных ниже пределов бесконечен:

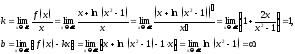
4. Находим производную и исследуем функцию на монотонность и локальные экстремумы. Имеем

Итак, 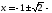критические точки. Применяя метод интервалов, будем иметь:

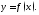Значит, в точке производная изменяет знак с плюса на минус, поэтому в этой точке функцияимеет локальный максимум, равный приближенноПо полученной информации строим график функцииОн буде иметь вид, указанный на рисунке выше. Чтобы закрепить на навыки, постройте график

(см. рисунок слева).