4. Применения формулы Тейлора

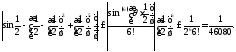
а) Приближенное вычисление значений функции. Если в формуле (4) (или (5)) отбросить остаточный член, то получим приближенное значение функции

с точностью до модуля остаточного члена. Если величина то и погрешность этого приближенного равенства будет очень малой. Например,При этом

б) Вычисление пределов.Ранее мы отметили, что при вычислении пределане достаточно формулы эквивалентности, так как при использовании этой формулы не

исчезает неопределенность. В таких случаях пользуются локальной формулой Тейлора (4), записывая в ней столько слагаемых, чтобы стало возможным ликвидировать неопределенность. В нашем примере поступаем так:

5. Правило Лопиталя

Другой способ раскрытия неопределенностей типа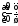илидоставляет такназываемое правило Лопиталя, к изложению которого мы переходим.

Теорема ЛопиталяПусть функции ив некоторой проколотой окрестностиудовлетворяют требованиям:

и непрерывны и дифференцируемы в

Если при этом существует(конечный или бесконечный) предел отношения производных: то и существует равный ему предел отношения самих функций:

Теорема ЛопиталяПусть функции ив некоторой проколотой окрестностиудовлетворяют требованиям:

и непрерывны и дифференцируемы в

Если при этом существует (конечный или бесконечный) предел отношения производных: то и существует равный ему предел отношения самих функций:

Например, для рассмотренного выше предела имеем

Лекция 4. Свойства функций, непрерывных на отрезке: ограниченность, достижение наибольшего и наименьшего значений, реализация всех промежуточных значений. Свойства дифференцируемой функции: монотонность, экстремумы. Схема построения графика функции с помощью первой производной

1. Свойства функций, непрерывных на отрезке

Функция называетсянепрерывной на отрезке если а) она непрерывна в любой точке а на концах иотрезка непрерывна справа и слева соответственно, т.е.Функции, непрерывные на отрезке, обладают рядом замечательных свойств, сформулированных ниже.

1. Теорема ВейерштрассаЕсли функция непрерывна на отрезкето она ограничена на этом отрезке, т.е. существует постояннаятакая, что

2. Теорема Вейерштрасса Если функция непрерывна на отрезкето она достигает на этом отрезке своих наибольшего и наименьшего значений, т.е. существуют точкитакие, что

3. Теорема Больцано-Коши Если функция 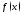непрерывна на отрезкето каково бы ни было значениесуществует значение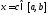такое, что

4. Теорема Больцано-Коши Если функция непрерывна на отрезкеи принимает на концах этого отрезка значения разных знаковто существует хотя бы одно значениетакое, что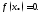

2. Монотонность функции

Напомним определение монотонных функций.

Определение 1. Говорят, что функция строго возрастает на множестве 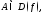если для любых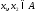из неравенствавытекает неравенствоЕсли жето функцияназываетсястрого убывающей на множестве Если же из строгого неравенствамежду аргументами вытекают нестрогое неравенствомежду значениями функции, то говорят, чтоявляетсянеубывающей (соответственно невозрастающей ) на множестве Множество всех функций строго возрастающих и строго убывающих образует класс строго монотонных функций; невозрастающие и неубывающие функции образует класс просто монотонных функций.

При исследовании на монотонность функций используются выписанная ранее

Теорема Лагранжа. Если функция непрерывна на отрезкеи является дифференцируемой по-крайней мере в интервалето существует точкатакая, что

Теорема 1. Пусть функция непрерывна на отрезке и является дифференцируемой по-крайней мере в интервалеТогда справедливы следующие высказывания:

1. если то функциястрого возрастает на отрезке;

2. если то функциястрого убывает на отрезке.

Доказательство вытекает из равенства (1), в котором надо положить Действительно, еслиа (тогда и), то (см. (1)) будет

выполняться неравенство Это означает, чтофункция строго возрастает на отрезке.Аналогично доказывается высказывание 2. Теорема доказана.

Замечание 1. Можно показать, что в случае нестрогого знака производной имеет место высказывание:

3. Для того чтобы функция 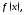удовлетворяющая условиям теоремы 1, была неубывающей (невозрастающей) на отрезке, необходимо и достаточно, чтобы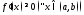(соответственно).

Например, функция строго убывает на любом отрезкетак какприи эта функция строго возрастает натак как при