Компьютерный практикум по статистике

ii) Двухфакторный дисперсионный анализ

При исследовании зависимости средней оценки Y по математической статистике в группе от метода обучения (A(1) — традиционный классический, A(2) — компьютерный, A(3) — комбинированный), будущего направления подготовки (B(1) — «Менеджмент», B(2) — «Социология») и их взаимодействия было выделе-

но случайным образом 18 групп, которые приписывались в равных количествах шести комбинациям методов и специальностей. Знания оценивались тестом, состоящим из 120 вопросов. Сведения о среднем числе правильных ответов в группах приведены в табл. 3.2.3.

Т а б л и ц а 3.2.3

B		B(1)			B(2)
A
A(1)	63	63	64	72	73	75
A(2)	65	68	69	79	79	80
A(3)	79	79	80	105	104	104

1.	Д е т е р м и н и р о в а н н а я м о д е л ь д в у х ф а к т о р н о г о
д и с п е р с и о н н о г о			а н а л и з а		(с п о в т о р е н и я м и) средней оценки
по математической статистике в группе имеет следующий вид:
	Y(i;j) = θ(0)	+ θ(i) + θ(j)		+ θ(i;j) + ε(i;j); i = 1, 2, 3; j = 1,2; k = 1, 2, 3,
	k	A	B	AB	k
где θ(0)	= MY , θ(Ai) , θ(Bj)		и θ(ABi;j) — неслучайные эффекты влияния на наблюде-

ние Yk(i;j) уровней A(i), B(j) факторов A и B и взаимодействия этих уровней, ε(ki;j) — случайный эффект влияния прочих неконтролируемых факторов.

К этой модели предъявляются следующие т р е б о в а н и я:

·все n = 3×3×2 = 18 случайных величин ε(ki;j) или, иначе, все 18 наблюдений Yk(i;j) должны быть независимыми;

·ε(ki;j) = N(0; σост ) или, иначе, Yk(i;j) = N (θ(0) + θ(Ai) + θ(Bj) + θ(ABi;j); σост ), т. е. при

каждой комбинации уровней факторов наблюдения должны проводиться в одинаковых («нормальных») вероятностных условиях с дисперсией, не изменяющейся при переходе от одной комбинации уровней факторов к другой;

	3	2	3	2
·	∑q(Ai) = 0 ,	∑q(Bj) = 0 ,	∑q(ABi; j) = 0 (j =1,2,…, nB ),	∑q(ABi; j) = 0 (i =1,2,…, nA ) .
	i=1	j=1	i=1	j=1

2. Введем исходные данные в рабочий лист Microsoft Excel (рис. 3.2.4). Для исследования модели воспользуемся программой «Двухфакторный дисперсионный анализ с повторениями», выбрав соответствующий пункт ме-

ню надстройки «Анализ данных».

В появившемся окне ввода данных (рис. 3.2.5) укажем входной интервал A1:C10, в который мы ввели исходные данные (с заголовками групп строк и столбцов — обозначениями уровней факторов), число строк для выборки

(число наблюдений при каждой комбинации уровней факторов — в данном случае 3), уровень значимости «Альфа» (по условию a = 0,05). Укажем, что

31

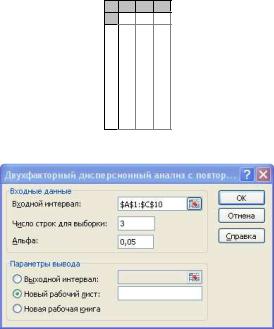
результаты работы программы необходимо вывести на новый рабочий лист.

Результаты работы программы представлены на рис. 3.2.6.

A B C

1B(1) B(2)

2	A(1)	63	72
3		63	73
4		64	75
		65	79
5	A(2)
6		68	79
7		69	80
8	A(3)	79	105
9		79	104
10		80	104

Рис. 3.2.4. Числовые данные для программы «Двухфакторный дисперсионный анализ с повторениями»

Рис. 3.2.5. Окно ввода данных программы «Двухфакторный дисперсионный анализ с повторениями»

Таблица «Дисперсионный анализ», полученная в результате работы

программы (рис. 3.2.6), представляет собой дисперсионную таблицу. В этой таблице «Выборка» — это фактор A, «Столбцы» — это фактор B, «Взаимодействие» — это взаимодействие факторов A и B, «Внутри» — это неконтролируемые факторы, «SS» — сумма квадратов, «df» — число степеней свободы, «MS» – средняя сумма квадратов, равная отношению SS к df, «F» — числовое значение статистики F, соответствующей проверяемой гипотезе, «P-значение» — это рассчитанный уровень значимости, «F критическое» — 100α%-ная критическая точка распределения Фишера — Снедекора с со-

ответствующими числами степеней свободы.

Расшифруем отдельные ячейки дисперсионной таблицы в табл. 3.2.4. В этой таблице

m

(i;j) =

∑yk(i;j)

i = 1, 2,…, ν

j = 1, 2,…, ν

k=1

,

,

;

y

A

B

m

νB

m

νA

m

∑∑yk(i;j)

∑∑yk(i;j)

(i) =

j=1 k=1

,

i = 1, 2,…, ν ;

(j) =

j=1 k=1

, j = 1,2,…,ν ;

y

y

A

mνB

A

B

mνA

B

В условиях задачи νA = 3, νB = 2, m = 3.

32

νA νB m

∑∑∑yk(i;j)

	=	i=1 j=1 k=1	.
y
		mνAνB

Двухфакторный дисперсионный анализ с повторениями
ИТОГИ	B(1)	B(2)	Итого
A(1)
Счет	3	3	6
Сумма	190	220	410
Среднее	63,33	73,33	68,33
Дисперсия	0,33	2,33	31,07
A(2)
Счет	3	3	6
Сумма	202	238	440
Среднее	67,33	79,33	73,33
Дисперсия	4,33	0,33	45,07
A(3)
Счет	3	3	6
Сумма	238	313	551
Среднее	79,33	104,33	91,83
Дисперсия	0,33	0,33	187,77
Итого
Счет	9	9
Сумма	630	771
Среднее	70,00	85,67
Дисперсия	53,25	203,50
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-значение	F критическое
Выборка	1839,00	2	919,50	689,625	4,12E–13	3,885
Столбцы	1104,50	1	1104,50	828,375	1,92E–12	4,747
Взаимодействие	199,00	2	99,50	74,625	1,7E–07	3,885
Внутри	16,00	12	1,33
Итого	3158,5	17

Рис. 3.2.6. Результаты работы программы «Двухфакторный дисперсионный анализ с повторениями»

Т а б л и ц а

3.2.4

Источник

Число степеней

Оценка дисперсии

вариации

Показатель вариации (SS)

свободы (df)

σ2

(MS)

величины Y

ост

νA

SSA

Фактор A

SS

= mν ∑(

(i) −

)2

= 1839

ν

– 1 = 2

s2

=

= 919,50

y

y

(выборка)

A

B

i=1

A

A

νA −1

A

νB

SSB

Фактор B

SS = mν

∑(

(j) −

)2 = 1104,5

ν

s2

=

= 1104,50

A

y

y

– 1 = 1

(столбцы)

B

B

B

B

νB

−1

j=1

Взаимодей-

νA

νB

2

SSAB

SSAB = m∑∑(

(i;j) −

A(i) −

B(j) +

)2 =199

(νA – 1)(νB – 1) =

sAB =

= 99

ствие факто-

(ν

−1)(ν

−1)

y

y

y

y

A

B

ров A и B

i=1 j=1

= 2

Остаточные

νA

νB

m

факторы

SSост

= ∑∑∑(yk(i;j) −

(i;j) )2 = 16

n – νAνB = 12

sост2 =

SSост

= 1,33

y

(внутри)

i=1 j=1 k=1

n − νAνB

νA

νB

m

Общая

SSитог

= ∑∑∑(

k(i;j) −

)2

= 3158,5

n – 1 = 17

y

y

вариация

i=1 j=1 k=1

33

SSитог

Проверим на 5%-ном уровне значимости гипотезу HA: θA(1) =θA(2) =θA(3) =0 об отсутствии влияния на среднюю оценку Y фактора A — метода обучения.

Наблюдаемое значение статистики

			=	s2	=	MS
	Fν −	−ν ν		A		выборка
				s2		MS
	A 1; n	A	B
				ост		внутри

равно 919,50/1,33 = 689,625.

Если гипотеза HA верна, то статистика FνA −1; n−νAνB имеет распределение

Фишера — Снедекора с nA – 1 = 2 и n – nAnB = 12 степенями свободы. При проверке гипотезы HA P-значение (которое приводится в результатах работы программы в таблице «Дисперсионный анализ» на рис. 3.2.6) равно вероятности P = P{F2; 12 > 689,25} = 4,12×10–13 (т. е. рассчитанному уровню значимости гипотезы HA), и гипотеза HA отвергается, поскольку P < a.

Другой способ получить тот же вывод — сравнить наблюдаемое значение статистики FνA −1; n−νAνB («F» из таблицы «Дисперсионный анализ» на рис. 3.2.6) с

соответствующей критической точкой fα; νA −1; n−νAνB («F критическое» из табли-

цы «Дисперсионный анализ»): гипотеза HA отвергается на 5%-ном уровне значимости, так как наблюдаемое значение статистики F2; 12 (в данном случае 689,625) больше критической точки f0,05; 2; 12 (в данном случае 3,885).

Аналогичным образом отвергаются гипотезы HB: θB(1) =θB(2) = 0 (об отсут-

ствии влияния на среднюю оценку Y по математической статистике фактора B — будущей специальности) и HAB (об отсутствии влияния на среднюю оценку Y взаимодействия метода обучения и будущей специальности). Та-

ким образом, метод обучения, будущая специальность и их взаимодействие влияют на среднюю оценку по математической статистике в группе. Оценим силу этого влияния, вычислив соответствующие коэффициенты детерминации.

	2		SSA	1839
	ˆ
3.	Поскольку коэффициент детерминации h	(Y | A) = SS		= 3158,5 =
			итог

= 0,58, то 58% общей вариации средней оценки Y обусловлено изменчивостью фактора A — метода обучения.

2		SSB	1104,5
ˆ
Так как h	(Y | B) = SS		= 3158,5		= 0,35, то 35% общей вариации средней
		итог

оценки Y обусловлено изменчивостью фактора B — будущей специальности.

Ввиду того, что ˆh2(Y | AB) = SSAB = 3158,5199 = 0,06 , 6% общей вариации

средней оценки Y обусловлено взаимодействием факторов A и B.

Влиянием неконтролируемых факторов обусловлен 100 – 58 – 35 – 6 =

=1% вариации средней оценки по математической статистике.

4.Оценки параметров детерминированной модели двухфакторного дисперсионного анализа с повторениями приведены в табл. 3.2.5.

34

Т а б л и ц а

3.2.5

Оцен-

Формулы и числовые зна-

Оцен-

Формулы и числовые значения

ˆ

y

77,83

θ

(1;1)

−

(1)

−

(1)

+

=

−

−

+

=

(0)

=

ˆ(1,1)

63,33

68,33

70,00

77,83

2,83

θ

AB

yAB

yA

yB

y

ˆ(1)

(1)

ˆ(1,2)

(1;2)

(1)

(2)

θA

yA

− y = 68,33 − 77,83 = −9,50

θAB

yAB

− yA

− yB

+ y = 73,33 − 68,33 − 85,67+ 77,83 = −2,84

ˆ(2)

(2)

ˆ(2,1)

(2;1)

(2)

(1)

θA

yA

− y = 73,33 −77,83 = −4,50

θAB

yAB

− yA

− yB

+ y = 67,33

− 73,33 − 70,00 + 77,83

= 1,83

ˆ(3)

(3)

ˆ(2,2)

(2;2)

(2)

(2)

θA

yA

− y = 91,83 − 77,83 = 14,00

θAB

yAB

− yA

− yB

+ y = 79,33 − 73,33 − 85,67+ 77,83 = −1,84

ˆ(1)

(1)

ˆ(3,1)

(3;1)

(3)

(1)

θB

yB

− y = 70,00 − 77,83 = −7,83

θAB

yAB

− yA

− yB

+ y = 79,33 − 91,83 − 70,00 + 77,83 = −4,67

ˆ(2)

(2)

ˆ(3,2)

(3;2)

(3)

(2)

θB

yB

− y = 85,67− 77,83 = 7,84

θAB

yAB

− yA

− yB

+ y = 104,33 − 91,83 − 85,67+ 77,83 = 4,66

sост2 =

= 1,15

sост

1,33

3.3. Ф о р м у л и р о в к а и р е ш е н и е в е р о я т н о с т н о - с т а т и с т и ч е с к и х з а д а ч

Приведем примеры содержательных задач, требующих применения вероятностно-статистических методов.

1. По данным о случайной величине X — ежемесячном суммарном вкладе населения в отделение банка за n = 9 месяцев вычислены выборочное среднее x = 100 тыс. ден. ед. и исправленное выборочное среднее квадратичное отклонение s = 8 тыс. ден. ед. Предполагая, что случайная величина X распределена по нормальному закону, требуется определить: а) вероятности того, что интервалы (0,9x;1,1x) и (0,8s;1,1s) накроют соответст-

венно математическое ожидание и генеральное среднее квадратичное отклонение случайной величины X; б) верхние границы для генеральной дис-

персии и для математического ожидания ежемесячного суммарного вклада (с надежностью 0,9).

Решение. Поскольку случайная величина Х распределена по нормаль-

ному закону, запишем:

−1,1

− MX

− 0,9

X

X

X

X

X

P{0,9X < a < 1,1X} = P{−1,1X < −a < −0,9X} = P

<

<

=

s

n

s

n

s n

= P{−

}= P{

}= P{

10

< Tn−1 <

10

Tn−1

<

10

T8

< 0,42} = 1− P{

T8

> 0,42} = 1− 0,69 = 0,31;

24

24

24

2

2

2

1

1

1

P{0,8s < σ < 1,1s} = P{0,64s

< σ

<

1,21s

} = P

<

<

=

σ2

1,21s2

0,64s2

n − 1

(n −1)s2

n −1

8

2

8

2

= P

<

<

= P

< χ

n−1

<

= P{6,61< χ

< 12,50} =

σ2

8

1,21

0,64

1,21

0,64

= P{χ82 > 6,61}− P{χ82 > 12,50} = 0,58

− 0,13 = 0,45.

Здесь вероятность P{

T8

> 0,42} = 0,69

можно найти с помощью стати-

стической функции

СТЬЮДРАСП

пакета

Microsoft Excel:

P{

Tk

> t} =

= СТЬЮДРАСП(t; k; 2) [последний параметр функции СТЬЮДРАСП означает

число хвостов распределения: если этот параметр равен единице, то функ-

35

ция СТЬЮДРАСП(t; k; 1) возвращает вероятность P{Tk > t} , а если он равен двойке, то функция СТЬЮДРАСП(t; k; 2) возвращает вероятность P{ Tk > t} = = P{(Tk < −t) (Tk > t)} = P{Tk < −t} + P{Tk > t}], а вероятности P{χ28 > 6,61} = 0,58 и P{χ28 > 12,50} = 0,13 можно определить с помощью функции ХИ2РАСП пакета

Microsoft Excel: P{χ2k > x} = ХИ2РАСП(x; k).

Вспомним определение процентных точек: 100p%-ная точка распределения «Хи-квадрат» с k степенями свободы — это такое число χ2γ;k , что

P{χ2k > χ2γ;k} = p .

Учитывая, что статистика

χ2	=	(n −1)s2
n−1		σ2

распределена по закону «Хи-квадрат» с n – 1 степенью свободы, запишем:

2

2

(n − 1)s2

2

2

(n − 1)s2

P{χn−1

> χγ; n−1} = γ P

> χγ; n−1

= γ P σ <

= γ.

2

2

σ

χγ; n−1

Таким образом, получаем, что односторонний доверительный интервал

для генеральной дисперсии σ2

(рис. 3.3.1) задается формулой

2

(n − 1)s2

P 0 < σ <

= γ.

2

χγ; n−1

P

0 < σ2

<

(n − 1)s2

= γ

2

χγ; n−1

σ2

(n − 1)s2

χ2γ; n−1

Рис. 3.3.1. Односторонний доверительный интервал для дисперсии

Найти 90%-ную точку χ2γ; n−1= χ20,9; 8 = 3,49 распределения «Хи-квадрат» с

восемью степенями свободы можно двумя способами:

∙либо с использованием таблицы процентных точек распределения «Хи-квадрат»: в такой таблице каждой комбинации вероятности p и числа степеней свободы k соответствует 100p%-ная точка χ2p;k распределения «Хи-квадрат» с k степенями свободы, т. е. такое число, что

P{χ2k > χ2p;k} = p ;

∙либо с помощью статистической функции ХИ2ОБР пакета Microsoft Excel: χ2p;k = ХИ2ОБР(k; p).

36

Подставив в формулу одностороннего доверительного интервала для

генеральной дисперсии σ2 значения γ = 0,9	, n = 9, s = 8, c2	= c2	= 3,49,
	g; n-1	0,9; 8

получим окончательно, что с вероятностью 0,9 генеральная дисперсия ежемесячного суммарного вклада окажется не больше чем

8×64 =146,7 тыс. ден. ед.

3,49

Перейдем к определению 90%-ной верхней границы математического ожидания ежемесячного суммарного вклада. Для этого рассмотрим статистику

Tn−1 = (X − MX)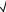n , s

которая имеет распределение Стьюдента с n – 1 степенью свободы.

Учтем, что 100p%-ная точка распределения Стьюдента с k степенями свободы — это такое число tp;k , что P{Tk > tp;k} = p, и примем во внимание,

что распределение Стьюдента симметрично, поэтому

P{Tk < -tp; k} = P{Tk > tp;k},

P{Tk > tp; k} = P{(Tk < -tp; k ) È (Tk > tp; k )} = P{Tk < -tp;k} + P{Tk > tp;k} = 2P{Tk > tp;k}.

Отсюда следует, что 100p%-ная точка tp;k распределения Стьюдента с

k степенями свободы равна двусторонней критической границе, соответствующей вероятности, в два раза большей: tp;k = t2p;k . В частности, 10%-ная

точка распределения

Стьюдента с

восемью

степенями

свободы

0,1; 8 = t2×0,1;8

= t0,2;8 = 1,40.

t

Далее запишем:

P{Tn-1 < -

t1-g; n-1} =1- g Û P{-Tn-1 > t1-g; n-1} =1- g Û

(

- MX)

(MX -

)

n

X

X

n

Û P -

> t

=

1- g Û P

> t

=1

- g Û

s

1-g; n-1

s

1-g; n-1

s

s

Û P MX > X

+ t

=1- g Û P MX < X

+ t

= g.

1-g; n-1

n

1-g; n-1 n

Таким образом, односторонний доверительный интервал для математического ожидания с надежностью γ задается формулой

s

P -¥ < MX < X + t

= g.

1-g; n-1

n

Подставляя в эту формулу значения

g = 0,9,

=100, s = 8,

0,1;8 =1,40,

t

x

найдем искомую 90%-ную верхнюю границу для математического ожидания ежемесячного суммарного вклада:

100 +1,40× 83 =103,7 тыс. ден. ед.

37

2. Клуб с большим количеством членов попал в некоторые финансовые трудности. Поэтому случайно были выбраны n = 500 членов этого клу-

ба, которым был задан вопрос, согласны ли они на небольшое увеличение взноса. Если более чем 275 из них согласятся на увеличение взноса, то правление клуба будет считать, что по крайней мере 60% всех членов клуба тоже будут за увеличение. Определить: а) вероятность ошибки первого рода, если в действительности 60% членов клуба будут за увеличение взноса; б) вероятность ошибки второго рода, если в действительности лишь 54% всех членов клуба будут согласны с запланированным увеличением взноса.

Решение. Пусть p — вероятность того, что случайно выбранный член клуба согласится на увеличение взноса. Гипотезу H0 : p = 0,6 принимают, если

m > 275 , где m — число членов клуба, согласных на увеличение взноса. Альтернативную гипотезу H1 : p < 0,6 принимают, если m 275.

По интегральной теореме Муавра — Лапласа вероятность ошибки

первого рода

a = P{H1 | H0} = P{m 275 | p = 0,6} = P{0 m < 276 | p = 0,6} =

276 - 500×0,6

0 - 500×0,6

= F0

- F0

= -0,486 - (-0,500) = 0,014.

500×0,6(1- 0,6)

500×0,6(1- 0,6)

Если альтернативное значение вероятности равно p = 0,54, то вероят-

ность ошибки второго рода

b = P{H0 | H1} = P{m > 275 | p = 0,54} = P{276 m < 501| p = 0,54} =

501- 500×0,54

276 - 500×0,54

F0

- F0

= 0,500 - 0,205 = 0,295 .

500×0,54(1- 0,54)

500×0,54(1- 0,54)

3. Торговая компания собирается открыть в новом районе города филиал. Из опыта работы компании известно, что филиал будет работать прибыльно, если за неделю средний доход жителей района превышает a0 = 400 ден. ед.; также известна дисперсия дохода s2 = 400 . Требуется:

а) определить правило принятия решения, с помощью которого, основываясь на выборке объема n = 100 и уровне значимости α = 0,05 , может быть

установлено, что филиал будет работать прибыльно; б) предположив, что в действительности средний доход за неделю составляет a1 = 406 ден. ед.,

рассчитать вероятность того, что при применении предложенного правила принятия решения будет совершена ошибка второго рода; в) считая альтернативное значение среднего недельного дохода равным a2 = 430 ден. ед.,

определить объем выборки, при котором риск ошибки первого рода не превысит 0,025, а риск ошибки второго рода не превысит 0,05.

Решение. Компания не откроет филиал, если средний доход жителей не превысит 400 ден. ед. Потому будем проверять гипотезу H0 :MX = a0 = 400 при альтернативной гипотезе H1 :MX > a0 . Так как значение генеральной

дисперсии s2 = 400 известно, то гипотезу H0 отвергают и принимают гипотезу H1, если наблюдаемое значение статистики

38

Z =

(

- a0 )

n

.

X

s

окажется больше критической точки u(1−2α)/2 .

Выполним следующие преобразования:

(

- a0 )

> u(1−2α)/2 Û

> a0 + u(1−2α)/2

s

.

n

Z > u(1−2α)/2

Û

X

X

s

n

По условию a0 = 400, критическая точка u0,45 = 1,65 [ее можно определить по таблице значений функции Φ0 (u) или с помощью статистической

функции НОРМСТОБР пакета Microsoft Excel], поэтому если X > 400 + +2×1,65 = 403,3, т. е. если недельный среднедушевой доход 100 жителей превысит 403,3 ден. ед., то это даст основание отвергнуть гипотезу H0 и принять гипотезу H1, т. е. принять решение об открытии филиала, если же X не

превысит 403,3 ден. ед., то оснований для открытия нового филиала нет. Если альтернативное значение среднего дохода a1 = 406 > a0, то вероят-

ность ошибки второго рода при альтернативной гипотезе H1:MX = a1 равна

b=0,5 - F0

(a1-a0)

n

-u(1−2α)/2

=0,5

- F0

6×10

-1,65

= 0,09.

s

20

Если же альтернативное значение среднего дохода a2 = 430 > a0 , то объем

выборки, при котором риск ошибки первого рода не превысит 0,025, а риск ошибки второго рода не превысит 0,05, рассчитаем, исходя из следующих соображений.

Запишем выражение для вероятности ошибки второго рода:

	b=0,5 - F0		(a2-a0)	n	-u(1−2α)/2
						.
			s

Будем считать вероятность ошибки первого рода заданной и равной a = 0,025 и запишем неравенство, выражающее требование того, чтобы ве-

роятность ошибки второго рода не превышала b = 0,05:

(a2-a0)

n

(a2-a0 )

n

b b Û 0,5 - F0

s

-u(1−2α)/2

b Û F0

s

-u(1−2α)/2

0,5

- b Û

(a2-a0)

1- 2

(a2-a0 )

n

Û F

n

-u

b

Û

-u

.

−

α

− α

u

(1−2β)/2

s

2

s

0

(1 2

)/2

(1 2

)/2

При последнем преобразовании мы учли, что 50(1- 2b)%-ная точка u(1−2β)/2 стандартного нормального закона определяется как из условия

F0 (u(1−2β)/2 ) = 1-22b ,

афункция Φ0 (u) монотонно возрастает.

39

Теперь можно определить минимальный объем выборки, который гарантирует, что вероятность ошибки первого рода будет равна α, а вероят-

ность ошибки второго рода будет не больше β :

(a2−a0)

n

− u

u

(a2−a0)

n

u

+ u

(1−2α)/2

(1−2α)/2

σ

(1−2β)/2

σ

(1−2β)/2

σ

(u(1−2α)/2 + u(1−2β)/2 ) n σ2

u

+ u

2

n

(1−2α)/2

(1−2β)/2

.

a2−a0

a2−a0

Подставляя в последнюю формулу a0 = 400, a2 = 430, σ = 400, α = 0,025 ,

= 0,05, u(1−2α)/2 = u0,475 = 1,96, u(1−2β)/2 = u0,45 = 1,65,

получим

неравенство для

β

объема выборки:

n 400

1,96 +1,65

2

430 − 400

или, окончательно, n 5,8 (т. е. при альтернативном значении среднего дохода a2 = 430 для обеспечения вероятности ошибки первого рода α = 0,025 и вероятности ошибки второго рода β 0,05 достаточно выборки из шести наблюдений)

4. Управляющий портфелем заботится о том, чтобы не осуществлять вложения в ценные бумаги с дисперсией годовой доходности, превышающей b0 = 0,04. Выборка из n = 51 наблюдения за доходностью некоторого актива показала, что исправленная выборочная дисперсия s2 = 0,045.

Требуется проверить на 5%-ном уровне значимости гипотезу о том, что доходность по данному активу характеризуется дисперсией, не большей 0,04, а также указать вероятность ошибочного заключения (при альтернативном значении дисперсии b1 = 0,045).

Решение. Проверим на 5%-ном уровне значимости гипотезу Н0: σ2 = = b0 = 0,04 при альтернативной гипотезе Н1: σ2 > b0.

Нулевую гипотезу можно отвергнуть на уровне значимости α, если

наблюдаемое числовое значение статистики

χ2n−1 = (n −1)s2

b0

окажется больше критической границы χ2α;n−1 .

В данном случае наблюдаемое значение статистики χ2n−1 равно

50×0,045 = 56,25,

0,04

а критическая точка χ20,05;50 = 67,50, поэтому на 5%-ном уровне значимости

нет оснований отвергнуть гипотезу о том, что доходность данного актива характеризуются дисперсией, не большей 0,04. При этом вероятность ошибки второго рода (при альтернативной гипотезе Н1: σ2 = b1 = 0,045) рав-

на

40