Математика, контрольная 1. Уч.пособ. 1 семестр

10. Введем новые переменные x + 3 = X и y − 7 = Y , тогда в новой системе координат XOY окружность примет вид X 2 + Y 2 = R2 . Центр ее совпадает с началом координат.

Рис. 2. Чертеж к заданию 4.

Задание 5

В этом задании рассматриваются вопросы аналитической геометрии в пространстве.

1) Уравнение плоскости, проходящей через три данные

точки A(xa ; ya ; za ) ; B(xв; yв; zв ) ;

формуле

x − xa		y − ya
xв	− xa	yв	− ya
xc	− xa	yc	− ya

C(xc ; yc ; zc ) находятся по

z − za

zв − za = 0 . zc − za

21

Ответ нужно представить в общем виде уравнения плоскости

Ax + Bx + Cz + D = 0 .

2) Для отыскания угла между прямой и плоскостью нужно: а) написать уравнение прямой, проходящей через две дан-

ные точки: A(xa ; ya ; za ) и D(xd ; yd ; zd ) , по формуле:

x − xa

=

y − ya

=

z − za

.

(23)

xd − xa

yd − ya

zd − za

Направляющий вектор этой прямой τ

= {m, n, p} имеет ко-

ординаты

m = xd − xa ; n = yd − ya ; p = zd − za .

б) угол α между прямой и плоскостью в пространстве на-

ходится по формуле:

Am + Bn + Cp

sin α =

;

A2

+ B2 + C2

m2 + n2 + p2

α = arcsin

Am + Bn + Cp

,

A2 + B2 + C 2

m2 + n2 + p2

где A, B, C - координаты нормального вектора

= {A, B, C} бе-

N

рутся из общего уравнения плоскости

Ax + By + Cz + D = 0 , как

коэффициенты перед x, y и z соответствено.

3)Уравнение прямой, проходящей через две точки, было приведено ранее (23).

4)Для того, чтобы найти уравнения высоты пирамиды,

опущенной из точки D на грань ABC , удобно воспользоваться каноническими уравнениями прямой в пространстве

x − x0 = y − y0 = z − z0 , m n p

где (x0 , y0 , z0 ) – координаты точки, лежащей на прямой. В данном случае нам известны координаты точки D{x, y, z} . Проекции направляющего вектора τ = {m, n, p} найдем из условия перпендикулярности прямой и плоскости. Так как вектор норма-

22

ли N к плоскости и направляющий вектор τ прямой параллельны, то в качестве направляющего вектора можно взять вектор

N{A, B, C} , т.е. τ = N{A, B, C}.

5) Основанием высоты является точка пересечения прямой, проходящей через высоту, с плоскостью основания ABC . Для нахождения этой точки пересечения решим систему уравнений:

x − x		0	=		y − y	0	=		z − z	0
	m				n				p
				+ Cz + D				= 0
Ax + By

Эту систему удобно решать, если перейти к уравнению прямой в параметрическом виде

x = x0 + mt
	+ nt
y = y0		(*)
	+ pt
z = z0

Подставим выраженные переменные ( x, y, z ) через t из

(*) в уравнение плоскости

A(x0 + mt) + B( y0 + nt) + C(z0 + pt) + D = 0 .

Отсюда найдем параметр t, подставим его в уравнение прямой и получим координаты искомой точки пересечения прямой с плоскостью.

Пример. В пирамиде из задания 2 найти: 1) уравнение плоскости АВС; 2) угол между ребром AD и гранью АВС; 3) уравнение прямой АВ; 4) уравнение высоты, опущенной из вер-

шины D на грань АВС; 5) основание этой высоты.

Решение.

1) уравнение плоскости выразим через определитель

	x − 0	y − (−7)	z −1
	1 − 0	0 − (−7)	− 7	−1		= 0 .
	3 − 0 − 5 − (−7)		− 4	−1
Решив его,		получим	уравнение грани (АВС)

23

19x +19 y +19z +114 = 0 . Отсюда находим вектор нормали

N{19, 19, 19} .

(24)

2) Для вычисления угла между ребром AD и гранью АВС

запишем сначала каноническое уравнение ребра AD

x − 0

=

y − (−7)

=

z −1

.

- 7 - 0

- 5 - (-7) 0 -1

Уравнение прямой AD :

x

=

y + 7

=

z −1

.

- 7

AD

2

-1

τ

Координаты

направляющего

вектора

вдоль

найдены выше (24).

= {−7, 2, −1} . Координаты нормали N

sin α =

(-19) × (-7) + (-19) × 2 + (-19) × (-1)

=

2

.

(-19)2 + (-19)2 + (-19)2

(-7)2 + 22 + (-1)2

3

2

α = arcsin

2

.

3

2

3) Уравнение прямой AB :

x − 0

=

y − (−7)

=

z −1

.

1 - 0 0 - (-7)

- 7 -1

После упрощения имеем -

x

=

y + 7

=

z −1

.

1

7

- 8

AB -

Координаты

направляющего

вектора

вдоль

τ

= {1, 7, − 8}.

4) Найдем уравнение высоты,

опущенной

из

вершины

D {−7; − 5; 0} на грань АВС, уравнение которой получено ранее

в (24).

|| τ

, то возьмем вектор τ

Так как

N

= N{19, 19, 19} ,

тогда

уравнение высоты

x + 7

=

y + 5

=

z

.

19

19

19

5) Решив систему уравнений

24

x + 7				y +	5			z
			=			=				,
				19			19
19
		+19 y +			19z +114 = 0
19x

найдем точку К, которая будет являться основанием высоты, опущенной из вершины D на грань АВС.

Для этого запишем уравнение прямой в параметрическом

виде

	x + 7		y + 5					x =19t - 7
						z
		=		=			= t ,	y =19t - 5 .	(25)
	19		19		19
								z =19t

Подставим в уравнение плоскости вместо переменных x, y, z их выражения через параметр t :

19(19 t - 7) +19(19 t - 5) +19 ×19 t +114 = 0 ,

1083t = 114 , t =	2	.	(26)
19
Теперь из (25) найдем x, y, z.

x =19 ×2 19 - 7
	× 2 19 - 5 , т. К {-5; -3; 2}.
y =19
	×2 19
z =19

ЗАДАНИЕ 6

В данном задании требуется вычислить пределы, не пользуясь правилом Лопиталя. Для этого рассмотрим некоторые теоретические сведения.

Если функция f (x) в окрестности точки x0 определена и непрерывна, то ее предел можно вычислить по формуле:

lim f (x) = f (x0 )

x→x0

Поэтому при вычислении пределов надо вначале убедиться, является ли функция f (x) непрерывной, или она разрывная в

25

окрестности точки x0 путем прямой подстановки x = x0 в выражение функции f (x) . Если f (x) не существует при x = x0 , то

тогда следует находить предел lim f (x) . Для этого применяют

x→x0

специальные приемы.

Разрывные функции часто имеют неопределенные значения в точке разрыва x = x0 . Неопределенности бывают следующих

	0		∞	3) 0 ×¥	∞
типов 1)	0	2)	∞		4) ∞ − ∞ 5) 1 . Это –	символическое

обозначение неопределенностей. Если функция имеет вид дроби

	f1 (x)			x = x0 числитель и знаменатель одновре-
		, у которой при
	f2 (x)
менно обращаются в ноль, т. е. f1 (x0 ) = 0 и							f2 (x0 ) = 0 ,		то такая
неопределенность обозначается					0	. Если же при		x ® x		имеем
					0			0
	f1 (x) ® ¥ и		f2 (x) ® ¥ одновременно, то неопределенность
обозначается			∞ . Функция может иметь				вид	произведения
	f1 (x) × f2 (x) .		∞			f1 (x0 ) = 0				x ® x0
			Если	при этом			и	при

f2 (x) ® ¥ , то такую неопределенность обозначают 0 ×¥ . Возможен случай, когда функция имеет вид разности [ f1 (x) - f2 (x)] ,

причем при x ® x0 f1 (x) ® ¥ и	f2 (x) ® ¥ одновременно.
Здесь возникает неопределенность	типа (¥ - ¥) . Еще может

быть вариант, когда функция имеет вид [ f (x)]ϕ ( x) и f (x0 ) = 1 , а при x ® x0 ϕ (x) ® ¥ . Такая неопределенность обозначается

1∞ . Для раскрытия подобных неопределенностей применяются специальные преобразования, которые допустимы правилами математики. После этого получаем выражения без неопределенностей и можно будет вычислить предел.

Для случая, когда f (x) имеет вид рациональной дроби и

26

x → ±∞ , имеем неопределенность типа ∞∞ , для вычисления ко-

торой надо числитель и знаменатель дроби поделить на старшую степень знаменателя.

Пример для задания а):

lim

5x5 − 9x3

+ 7x − 26

. Имеем

неопределенность вида ∞∞ .

x→∞ 91 + 2x + 8x4 −13x5

Чтобы

раскрыть

эту

неопределен-

ность разделим числитель

и

знаменатель

на

x5 .Получим

lim

5 − 9 / x2 + 7 / x4 − 26 / x5

. Так как при x →∞ A xα → 0 (α > 0) ,

x→∞ 91/ x5 + 2 / x4 + 8 / x −13

то имеем lim

5 − 9 / x2 + 7 / x4 − 26 / x5

= −

5

.

x→∞ 91/ x5 + 2 / x4 + 8 / x −13

13

f (x) ϕ (x) , у

Во втором примере функция имеет вид дроби

которой числителем и знаменателем являются рациональные выражения, которые содержат только целые положительные степе-

ни переменной

x . Если при

x = x0

числитель

f (x0 ) = 0

и зна-

менатель ϕ (x0 ) = 0 , то

f (x)

и ϕ (x) нацело (без остатка) делят-

ся на разность ( x − x0 ). Это деление осуществляется углом.

Пример для задания б): lim

3x3 − 4x2 + 1

. Так при

x = 1

x→1 2x2 + 5x − 7

(

3x3 − 4x2

)

x=1

= 0 и

(

2x2 +

5x − 7

)

x=1

имеем

+ 1

= 0 , то

3x3 − 4x2 + 1

x −1

− 3x3 − 3x2

3x2 − x −1

2x2

+ 5x − 7

x −1

−

2x

+ 7

−

− x2 + 1

2x2 − 2x

− x2 + x

−

7x − 7

.

−

− x + 1

7x − 7

− x + 1

0

0

27

Теперь числитель и знаменатель первоначальной дроби можно представить произведением, что помогает вычислить предел

lim	3x3	- 4x2 +1		= lim	(3x2 - x -1)( x -1)	= lim	(3x2 - x -1)	=	1
					(2x + 7)( x -1)		(2x + 7)			.
		+ 5x - 7							9
x→1 2x2				x→1		x→1

В третьем примере (в) вычисляется предел при x ® 0 для

неопределенности типа 0 с участием тригонометрических функ-

0

ций. Для выполнения этого задания следует использовать первый замечательный предел или его разновидности

lim	sinα	=1 ,		lim		tg α	=1 , lim		arcsinα		=1,
α →0	α			α →0 α				α →0		α
	lim		sin kα		= k ,		lim	arctgα		=1 .
								α
	α →0		α				α →0

Кроме того нужны некоторые формулы из тригонометрии sin 2α = 2sinα ×cosα , 1 - cosα = 2sin2 α , sin2 α + cos2 α =1.

Пример для задания в):											2
				2sin	2 9							sin	9		2
	1 - cos9x							x		2				x			2		9 2
						2							2
lim			= lim						=		lim					=				.
	3x	2		3x		2				3		x
x→0			x→0								x→0						3		2

В заданиях (г) требуется раскрыть неопределенность типа

1∞ , либо 0 ×¥ . Для их вычисления следует использовать второй замечательный предел

		1	x	1
lim 1	+			= e ; lim (1 +α ) α = e
x→±∞		x		α →0

и свойства логарифмов

ln A - ln B = ln A ; k × ln A = ln Ak .

B

Примеры для задания г):

		2x - 5 x−2			2x + 6 -11 x−2				11 x−2
1)	lim			= lim			= lim 1	-			=
	x→∞	2x + 6		x→∞	2x + 6		x→∞		2x + 6

28

	1			11		11
= Обозначим			= -		, x = -			t - 3 , при	x ® ¥ t ® ¥	=
				2x + 6
		t				2

11

11

− 2

1+

1

−

2

t −5

1+

1

−5

1+

1

t

−

11

−

11

= lim

= lim

×lim

=1×e 2 = e

2 .

t →∞

t →∞

t →∞

t

t

t

( x + 3)

lim (2x +1)

ln ( x + 3)

- ln ( x +1) = lim

(2x +1)ln

=

x→∞

x→∞

( x +1)

2)

2

2

2 x+1

= lim

(2x +1)ln 1

+

= lim ln 1 +

x

x +1

x→∞

+1

x→∞

Так как функция ln x

непрерывная, то можно перейти к

пределу под знаком функции, т.е.

2 2 x+1

2

2 x+1

lim ln 1 +

= ln lim

1 +

=

x→∞

x +1

x→∞

x +1

1

2

Обозначим

=

, x =

2t -1 ,

при x ® ¥ t ® ¥ =

t

x +1

1 +

1

4t −1

1 +

1

−1

1 +

1

t 4

= ln lim

= ln lim

× lim

= ln e4

= 4

t →∞

t

t →∞

t

t →∞

t

ЗАДАНИЕ 7

Для нахождения производных необходимо знание основных формул дифференцирования.

Правила дифференцирования

Пусть u = u ( x) , v = v( x) , w = w(x) , тогда

y = Cu,

′

′

′

′

′

′

y

= Cu ;

y = u + v - w, y

= u

+ v

- w ;

y = u × v,

y′ = u′ × v + u × v′ ;

y =

u

,

y¢ =

u′ × v - u × v′

;

y =

C

,

y¢ = -

Cv′

;

v2

v

v2

v

Производная сложной функции y = F (u ( x)), y¢ = Fu¢(u )u¢x ( x) .

29

Таблица производных

y = C, y′ = 0 ; y = un , y¢ = n × un−1 × u¢ ;

y = sin u, y′ = cos u × u′ ;

y = cos u, y′ = -sin u × u′ ;

y = tg u, y¢ =

u′

;

y = ctg u, y¢ = -

u′

;

cos2 u

sin2

u

y = loga u, y¢ =

u′

; y = ln u, y¢ =

u′

;

u

× ln a

u

y = au , y¢ = au × ln a × u¢ ; y = eu , y¢ = eu × u¢ ;

y = arctg u, y¢ =

u′

;

y = arcctg u, y¢ = -

u′

;

+ u2

1 + u2

1

y = arcsin u, y¢ =

u′

;

y = arccos u, y¢ = -

u′

;

1

- u2

1 - u2

формула для логарифмического дифференцирования

		y = uv , ln y = v ×lnu, (ln y)¢ = (v ×lnu)¢ ,
y¢			v			v	u¢		(27)
		= v¢×lnu +		u¢,	y¢ = u	v¢×lnu +v		.
y
			u				u

Примеры для заданий а) и б):

y=e-2x × sin8x × tg2 x . Находим производную от произведения функций.

y¢ = (e−2x 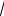sin8x )¢ tg2 x + e−2x sin8x (tg2 x)¢ = (e−2x )¢ sin8x tg2 x +

+e−2x (sin8x )¢ tg2 x + e−2x sin8x (tg2 x)¢ = e−2x (-2x)¢ sin8x tg2 x + +e−2x ((sin8x)¢(2sin8x ))tg2 x + e−2x sin8x 2tg x(tg x)¢ = -2e−2x ´

´sin8x tg2 x + e−2x (8cos8x (2sin8x ))tg2 x + e−2x sin8x × 2tg x /

/ cos2 x = 2e−2x tg x(-sin8x tgx + 2cos8x × tgxsin8x + sin8xcos2 x).

		1-ln2 x					1-ln2 x			1 3
y= 3						=				.
		1+sin	3	2x			1+sin	3
									2x

30