Лекция 16. Построение графиков функций

Лекция 16.

Исследование функции и построение эскиза её графика. Кривизна графика в точке.

Для наглядного описания функции часто используют её графическое представление. Как правило, такое представление бывает полезно для обсуждения качественных вопросов поведения исследуемой функции. Например: где функция пересекает ось ОХ, ось ОУ; на каких интервалах она возрастает и на каких убывает; есть ли у неё локальные экстремумы; каково направление выпуклости графика; имеются ли разрывы графика; какова асимптотика и так далее. Для точных расчетов графики функций используются редко. Однако бывает очень полезно изучить график перед проведением точных расчётов, так как из графического поведения функции видно какие алгоритмы и вблизи каких точек графика применять наиболее целесообразно. Для построения графика дифференцируемой функции y f x используют алгоритмы дифференциального

исчисления. Рекомендуемый порядок исследования функции и построения её графика приведён ниже.

1)Указать область определения функции D f x .

2) Указать нули функции, если это возможно.

3)Отметить конкретные особенности: чётность, периодичность.

5)Найти промежутки монотонности функции и указать её локальные экстремумы. 6)Уточнить характер выпуклости графика и указать точки перегиба графика. 7)Выяснить асимптотическое поведение функции: с указанием уравнений

вертикальных и наклонных асимптот.

8) Отметить характерные точки графика, например, точки пересечения графика функции с осью ОУ, если они есть и их возможно вычислить. Очень полезно вычислить две, три конкретные точки графика функции.

Рассмотрим примеры.

Пример 1. Исследовать функцию y

x5

5x3 и построить её график

1.

Данная функция есть многочлен пятой степени. Область определения D многочлена

интервал

;

2.

Определим нули функции. В данном случае это возможно

x5 5x3

x3 x2 5 x3 x

5 x

5 0, x

5; x 0; x

5

1

2

3

3.Функция нечётная, так как

y x x 5 5 x 3 x 5 5x3 ( x 5 5x3 ) y x

4. Определим участки монотонности и локальные экстремумы. Вычислим критические

точки функции.	У многочлена у всех критических точек y 0 . Отсюда
y 5x4 15x2
	0 x	3; x 0; x			3
	1	2		2

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

5x4

15x2

5x2 (x2

3) 5x2 x

Производная

y

3 x

3 положительна

на интервалах

;

3

3;

. Производная отрицательна на интервалах

3; 0

0;

3

. Вычисляем значения функции в критических точках

y

3

10.4;

y

0

0; y 3

10.4 и заполняем таблицу.

-

3

0

3

x

y

+

0

-

0

-

+

y

10.4

0

-10.4

Используя правило 1.1 нахождения локальных экстремумов с помощью первой производной

получаем. При х =- 3 локальный максимум, при х=0 экстремума нет, при х= 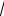3 локальный минимум.

5.Исследуем функцию на выпуклость. Для этого используем правило 1.2. Вычисляем вторую производную, приравниваем её нулю и находим точки «подозрительные на перегиб».

20x3

10x 2x2

y

30x

0

3

0

x

0, x

1.5

1.2, x

1.5 1.2

1

2

3

Вторая производная

y

20x3

30x

0

10x 2x2 3

положительна

на интервалах

1.5;0

1.5;

Производная отрицательна на интервалах

; 1.5

0; 1.5

.Определяем точки подозрительные на перегиб.

Вычисляем значения функции в точках подозрительных на перегиб

y

3

10.4; y

0

0; y

3

10.4 и заполняем таблицу.

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

		- 1.5			0		1.5
x
y	-	0		+	0	-	0	+
y		-6.4			0		6.4

Используя правило 1.2 нахождения точек перегиба с помощью второй производной, получаем,

что точки	1.5; 6.4 ; 0;0 ; 1.5;6.4 являются точками перегиба графика функции.

6.Исследуем функцию на асимптотическое поведение. Многочлен не имеет асимптот.

7.График пересекает ось ОУ в точке (0,0).

8.Используя таблицы, строим график функции

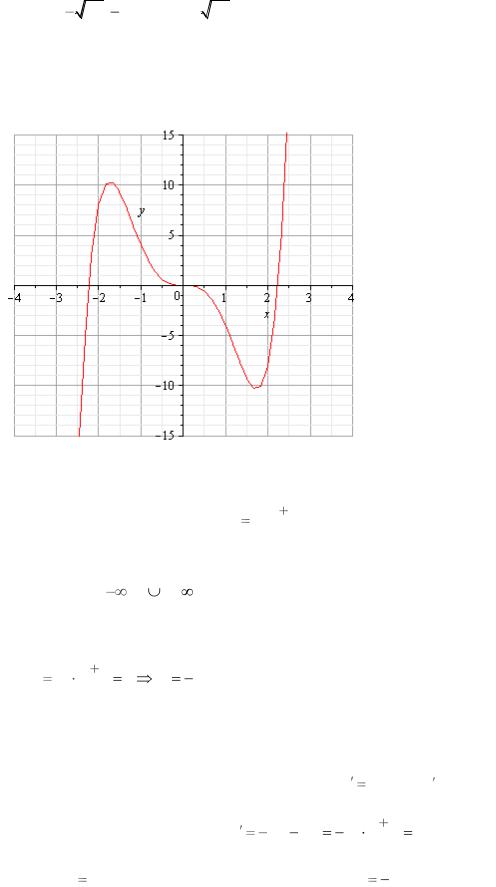
Пример 2. Исследовать функцию y

12x

36

и построить её график

x2

1. Данная функция это дробнорациональная функция. Область определения D есть

множество

;0)

(0;

2. Определим нули функции. В данном случае это возможно

y 12

x

3

0

x

3;

x2

1

3.Функция общего вида

4. Определим участки монотонности и локальные экстремумы. Вычислим

критические точки функции. В этих точках либо

y

0 , либо y не существует.

Вычисляем производную функции y

12

72

12

x 6

0 .

x2

x3

x3

В точке x1

0 производная не существует . В точке x2

6 производная равна нулю .

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

Производная y

12

36

12

x

6

положительна

x2

x3

x3

на интервале

;

6 . Производная отрицательна на интервалах

6;0

0;

. Вычисляем значения функции в критических точках.

В точке x

6 , y

6

1 , в точке

x

0 значения функции не существует.

Заполняем таблицу.

x

-6

0

y

+

0

-

0

-

y

-1

0

Используя правило 1.1 ( нахождения локальных экстремумов с помощью первой производной)

получаем. При x 6 локальный минимум, при х=0 экстремума нет.

5. Исследуем функцию на выпуклость. Для этого используем правило 1.2. Вычисляем вторую производную, приравниваем её нулю и находим точки «подозрительные на перегиб». Вторая

производная равна y		24(x 9)		. В точке
		x4
x	9вторая производная y			0, в точке x	0, y не существует . Точка подозрительная
на перегиб имеет координаты (			9; 0.9) . Определяем знаки y			x на интервалах.
y	x положительна	на интервалах 9;0			0; . y x	отрицательна на интервале

; 9 . Согласно правилу 1.2 точка ( 9; 0.9) является точкой перегиба графика.

Для определения знаков второй производной применяем метод интервалов и заполняем соответствующую таблицу

x		-9		0
y	-	0	+	нет	+
y		-0,9		нет

6. Находим асимптоты графика функции. Асимптота это прямая, к которой

неограниченно приближается график функции при x	. Наклонная асимптота имеет
уравнение y kx b . Алгоритм нахождения параметров k и b	известен.

Сначала определяем

k : k

lim

y

12 lim

x 3

применяем правило Лопиталя

12 lim

1

12 0 0

.

x

x

3

3x

2

x

x

x

Затем определяем

b :b

lim 12

x

3

0

x

правило Лопиталя 12 lim

1

12 0

0

x

2

2x

x

x

Уравнение наклонной асимптоты найдено y

0 .

При x

график также имеет асимптоту y

0 .

Легко находим, что x

0 есть уравнение вертикальной асимптоты

lim 12

x

3

12 lim

x

3

lim

1

36

;

x2

x2

x 0

x 0

x 0

lim 12

x

3

12 lim

x

3

lim

1

36

;

x2

x2

x 0

x 0

x 0

7.График не пересекает ось ОУ.

8.Используя таблицы, строим график функции

Пример 3. Исследовать функцию y	x	5	2	и построить её график
	x	1

1. Данная функция это дробнорациональная функция. Область определения D есть

множество

;

1) (

1;

2. Определим нули функции. В данном случае это возможно

y

x

5

2

0

x

5

x

1

3.Функция общего вида .

4.с помощью первой производной определяем участки монотонности и локальные

экстремумы. Вычисляем

критические точки функции. Стационарными точками являются

точки, в которых y

x

0

: y x

x

5 2

x 5

x

7

0 x1

7; x2 5

x

1

x

1 2

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

	x			-7				5
	y		+	0		-		0				+
	y			-24				0
Используя правило 1.1 нахождения локальных экстремумов												получаем. При х=-7 локальный
максимум, при х=5			локальный минимум.
5. С помощью второй производной y						x		72			исследуем функцию на выпуклость.
							x	1	3

Находим точки «подозрительные на перегиб»
Точки, в которых производная равна нулю отсутствуют y	x	0 : y
Точка, в которых вторая производная не существует x0	1 .

Для определения знаков второй производной слева и справа от точки x метод интервалов и заполняем соответствующую таблицу

		-1
x
y		нет
			+
y		нет

	72	0 .
	x 1 3

1 применяем

Точек перегиба графика нет.

6. Исследуем поведение функции на бесконечности.

Находим наклонную асимптоту. Асимптота это прямая, к которой неограниченно

приближается график функции при x

. Наклонная асимптота имеет уравнение

y

kx

b . Алгоритм нахождения параметров k и b

известен.

Сначала определяем

k :

k

lim

y

lim

x

5 2

применяем правило Лопиталя

lim

2 x

5

x

x

1 x

2x

1

x

x

x

.

применяем правило Лопиталя

lim

2

1

2

x

Затем

b :b

lim

x 5

2

1 x

lim

x 5 2

x2 x

lim

3x 25

x 1

x

1

x 1

x

x

x

применяем правило Лопиталя

3

Уравнение наклонной асимптоты найдено

y x 3

Проверим , имеет ли данная функция вертикальную асимптоту.

Прямая,	имеющая уравнение x x0							называется вертикальной асимптотой графика
функции y	x		если y x			бесконечно большая при x				x0 или x x0 .
Так как	lim		x	5 2		; lim	x	5 2	, то
			x	1			x	1
x		1				x 1
прямая	x		1 является вертикальной асимптотой.

7.График пересекает ось ОУ в точке (5,0). 8. Строим график функции.

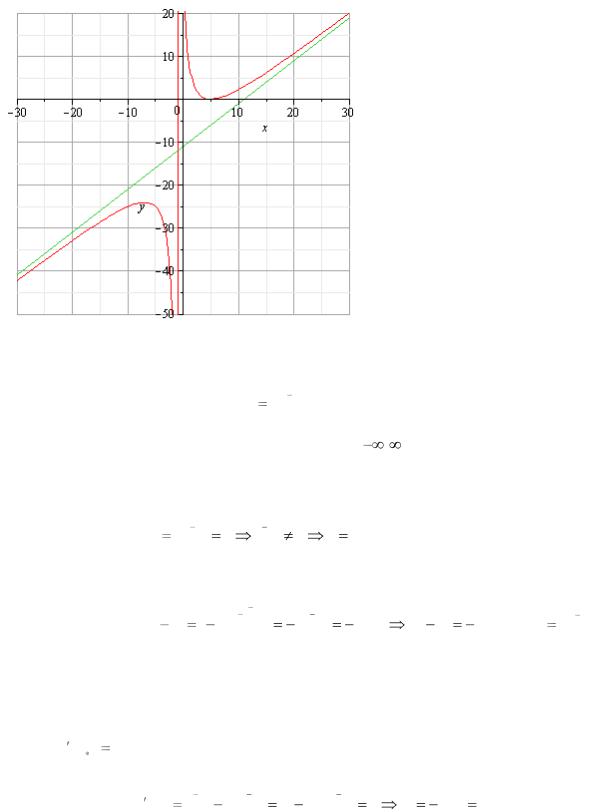
						x2
Пример 4. Исследовать функцию			y	xe		2		и построить её график
1. Область определения D функции интервал									;
2.Определим нули функции. В данном случае это возможно
	x2			x2
y xe 2 0			e	2		0		x	0

			x 2		x2				x2
3.Так как	y x	x e 2		xe 2		y x	y x	y x , то y xe 2

функция нечётная.

4.С помощью первой производной определяем участки монотонности и локальные

экстремумы. Вычисляем		критические точки функции.							Такими точками являются точки в
которых y x	0 :
			x2		x2		x2
	y x	e 2		x2e 2		1 x2 e 2 0			x	1; x 1
									1	2

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

		-1		1
x
y		0	+	0
y		-0,6		0,6

Используя правило 1.1 нахождения локальных экстремумов с помощью первой производной

получаем. При х=-1 локальный минимум, при х=1

локальный

максимум.

5.С помощью второй производной исследуем функцию на выпуклость. Находим точки

«подозрительные на перегиб».В этих точках y

0 или не существует

x2

x2

x2

x2

y ( 1 x2 e 2 )

2xe 2 x 1 x2 e 2

e 2 (x3

3x) 0 x

3; x

0; x

3

1

2

3

Для определения знаков второй производной слева и справа от этих точек применяем метод интервалов и заполняем соответствующую таблицу

						0
		- 3							3
x
y		0				0		0				+
					+
y		нет

4. Исследуем функцию на асимптотическое поведение.

Находим наклонную асимптоту. Асимптота это прямая, к которой неограниченно

приближается график функции при x

. Наклонная асимптота имеет уравнение

y kx b . Алгоритм нахождения параметров k и b

известен

y

x2

1

1

Сначала всегда определяем k :

k

lim

lim e

2

0 .

x

x

2

x

x

lim e 2

x

x2

x

1

1

Затем b : b lim

xe 2

0 x

lim

П.Л.

0

x

2

x

2

x

x

e 2

lim xe 2

x

П. Уравнение наклонной асимптоты найдено y

0

x2

Так как функция y

xe 2

непрерывна, то вертикальных асимптот нет.

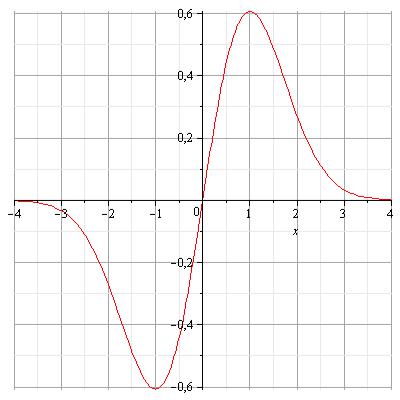
7. График пересекает ось ОУ в точке (0,0).

8. Строим график функции.