математика Раздел1 практика

РЕШЕНИЕ: Искомым геометрическим местом будет парабола. Напишем ее уравнение. Пусть М (x; у) – произвольная точка геометрического места. По условию MF = MN, где N – основание перпендикуляра, опущенного из точки M на прямую у = –5.

Так как

MF	x2		( y 3)2 и MN			( y ( 5))2 ,
то
		x2	( y 3)2		( y 5)2 ,
откуда
x2		y 2	6 y 9 y 2			10y 25 .

Приводя подобные члены, получим уравнение параболы x2 16y 16 .

Задания для решения:

1. Найти каноническое уравнение эллипсов по следующим данным: а) большая полуось равна 10 и эксцентриситет равен 0,8;

б) малая полуось равна 12 и эксцентриситет равен 135 ;

в) эксцентриситет равен 0,6, расстояние между фокусами 6; г) сумма полуосей равна 18 и расстояние между фокусами 12.

2. Определить длины осей, координаты фокусов и экцентриситеты эллипсов, заданных уравнениями:

а) 9х2	+ 25у2 = 225;
б) 9х2	+ у2 = 36.
			x2			y2
3. Написать уравнения директрис эллипса							1 .
		125			100

4.Написать канонические уравнения гипербол, если известно, что:

а) расстояние между фокусами равно 10 и эксцентриситет 53 ;

б) действительная полуось равна 20 и гипербола проходит через точку М (–10; 4);

5. Найти длины осей, координаты фокусов и эксцентриситеты гипербол, заданных уравнениями:

а) 144х2 – 25у2 = 3600; б) 9у2 – 16х2 = 144.

		x2		y2
	6. Дан эллипс				1	. Найти уравнение гиперболы, вершины
		9	6

которой находятся в фокусах, а фокусы – в вершинах данного эллипса. 7. Написать уравнение параболы, зная, что:

31

а) парабола симметрична относительно оси Ох, проходит через точку N (–3, 6) и начало координат;

б) парабола симметрична относительно оси Оу, проходит через точку N (6, 3) и начало координат;

8. Найти координаты фокусов и уравнение директрисы параболы,

заданной уравнением:

а) у2 = 6х;

б) х2 = 4у;

в) у2 =– 6х;

г) х2 = 4у.

32

Тема 1.10 Плоскость в пространстве. Задачи на составление уравнений плоскостей в пространстве.

Уравнение		плоскости,	Уравнение плоскости, проходящей через
проходящей	через	точку	три точки M1 (x1; y1; z1), M2 (x2; y2; z2),
M0 (x0; y0; z0) и перпендикулярной			M3 (x3; y3; z3):
вектору n ( A; B;C) :

		ьный
	мал
р
Но		ктор
	ве

		;C)
	;B
n	(A

	)				)
					;z3
	;z2				;y3
;	y2			x3
			(
(x2		M3
M2
			z )
		; 1
	;y1
	(x1
M1

	z )
; 0
;y0
(x0
M0

A(x x0 ) B( y y0 ) C(z z0 ) 0

.

Уравнение					плоскости				в
отрезках:
					z
				c
					b
		a					y
x
	x		y			z	1.
	a		b			c

x	x1	y	y1	z	z1
x2	x1	y2	y1	z2	z1	0 .
x3	x1	y3	y1	z3	z1

Общее уравнение плоскости:

					й				;C	)
				ы
			н					A	B
		аль
	м						(	;
						n
р			тор
Но
		ек
	в

Ax By Cz D 0 .

Образцы решения задач:

ПРИМЕР	Составить уравнение	плоскости,		перпендикулярной			вектору
			M0 (5; 2; –3).
n (2; 1; 4)	и проходящей через	точку			Лежат	ли	на этой
плоскости точки Р (1, 2, –1), Q (4, 5, 1) и R (–6, 2, –3)?
РЕШЕНИЕ: Подставляя в уравнение A(x			x0 )	B( y y0 )	C(z	z0 )	0

значения А = 2, B = –1, С = 4, х0 = 5, у0 = 2, z0 = –3, получим 2 (х–5) – (у–2) + 4 (z+3) = 0.

Раскрывая скобки и приводя подобные члены, находим искомое уравнение плоскости

2х – у + 4z+4 = 0.

Выясним, лежат ли точки Р, Q и R на данной плоскости. Подставляя последовательно координаты этих точек в левую часть последнего уравнения, получим:

33

2	1	1 2	4	(	1)		4	0;
2	4	1 5	4 1			4	0;
2	(	6) 1 2			4	(	3)	4 0.

Следовательно, точка Р лежит на данной плоскости. Точки Q и R плоскости не принадлежат. Они находятся по разные стороны от нее (в результате подстановки их координат в уравнение плоскости получены числа разных знаков).

ПРИМЕР Определить отрезки, отсекаемые плоскостью 2х – 3у + 8z – 4 = 0 на осях координат.

РЕШЕНИЕ: Разделив обе части уравнения на 4, получаем:

	x	3		y	2z 1 или		x				y						z	1.
2			4			2						4					1
											3						2
Сравнивая последнее уравнение с уравнением													x				y		z		1, находим:
													a				b		c
				a	2, b	4		, c				1		.
						3					2

ПРИМЕР Составить уравнение плоскости, проходящей через три данные

точки M1 (x1; y1; z1), M2 (x2; y2; z2), M3 (x3; y3; z3). Написать уравнение для случая M1 (1; 3; –2), M2 (4; –5; 6), M3 (–3; 1; 2).

РЕШЕНИЕ:

)

)

;z3

;z2

;y3

;

y2

x3

(

x2

3

(

M

M

2

)

)

;z1

;y1

y

;z

x1

;

(

1

x

M

(

M

			r
	r2	r3
r1

O

	Пусть	М	–		произвольная				точка	плоскости и
r1	OM1 , r2	OM 2 , r3	OM3 ,		r	OM	– радиус – векторы точек M1, M2, M3,
M.
Введем в рассмотрение векторы:
		M1M 2	r2	r1	,	M1M3	r3	r1	, M1M r r1.

Поскольку эти три вектора лежат в одной плоскости, то их смешанное

произведение равно нулю, т.е.
(r r1 )(r2			r1 )(r3		r1 ) 0.
			34

Это уравнение в координатной форме имеет вид:

					x	x1		y	y1	z		z1
					x2	x1		y2	y1	z2		z1		0 .
					x3	x1		y3	y1	z3		z1
Уравнение плоскости, проходящей через												точки		M1 (1; 3; –2), M2 (4; –5; 6),
M3 (–3; 1; 2) в соответствие с приведенной выше формулой имеет вид:
	x 1		y 3 z 2								x 1 y 3 z 2
	4	1	5	3		6	2		0 или			3		8	8	0 .
	3	1	1	3		2	2					4		2	4

Разлагая последний определитель по элементам первой строки, получим:

(x 1)	8	8	( y 3)		3 8		(z 2)	3	8	0
	2	4			4	4		4	2
			8x 22y		19z		36 0.

ПРИМЕР Составить уравнение плоскости, проходящей через точки

M1 (1; –2; 6), M2 (5; –4; –2) и отсекающей равные отрезки на осях Ох и Оу. РЕШЕНИЕ: Уравнение плоскости ищем в виде

x		y		z	1.
a		b		c

По условию a = b, поэтому уравнение можно записать так:

x		y		z	1.
a		a		c

Подставляя координаты точек M1 и M2 в последнее уравнение, получим

	1		2				6		1,									5				4			2		1
		a		a			c											a					a			c
	или
						1				6					1,				1				2		1.
						a				c									a				c
	Решая полученную систему уравнений, находим с = 2, a																											1	.
																												2
	Следовательно, искомое уравнение имеет вид
									x						y				z			1
									1						1			2
									2						2
	или
					4х + 4у + z – 2 = 0.

Задания для решения:

1. Составить уравнение плоскости, проходящей через точку M (2; –1; –4)

и перпендикулярной вектору n (3; 6; 1) , в векторной и координатной формах.

2. Определить отрезки, отсекаемые на осях координат плоскостями:

а) 2х – 3у + 4z – 24 = 0.

35

б) 4х + у – 3z – 2 = 0.

3.Построить плоскости:

а) 2х + 3у – 4z – 12 = 0; б) 2х – 3у – 6 = 0; в) 4х + 5у = 0; г) 4х + 9 = 0.

4.Составить уравнение плоскости, проходящей через точку M (4; –3; 5),

иотсекающей на осях координат равные отрезки.

5.Написать уравнение плоскости, проходящей через три точки:

L (–2; 4; 1), M (0; 2; –1), N (2; 0; –1).

6. Составить уравнение плоскости, проходящей через точку M1 (x1; y1; z1)
				(b ; b ; b ).
и параллельной двум неколлинеарным векторам a	(a ; a ; a ), b
	1	2 3		1 2	3
Написать уравнение в случае, когда M1 (2; –1; 3), a	(1;	1; 2),	b	(2; 1;	3).

36

Тема 1.11 Прямая в пространстве. Задачи на задание прямых в

пространстве. Задачи на взаимное расположение прямой и плоскости в

пространстве.

Канонические уравнения прямой:

Параметрические уравнения прямой:

й

й

и

щ

ы

ю

ьн

я

авл

л

а

р

м

р

тор )

Нор

о

п

т

а

к

p

к

)

zн

ве

е

;

в

C

n

;

B

;

m

z)

;

;y

;

A

(

(

s

M

(x

n

z )

z

; 0

;y0

(x0

M0

l

;y;

z)

y

M

(x

z )

; 0

;y0

(x0

M0

x

l

y

x

x0

y

y0

z

z0 .

x

m

n

p

x

x0

mt,

y

y0

nt,

z

z0

pt.

Уравнение прямой, проходящей через две данные точки:

z

)

z2

;

y2

;

2

x

(

2

M

)

z1

;

y1

;

1

x

(

1

l M

x

x

x1

y

y1

z

z1 .

x2

x1

y2

y1

z2

z1

37

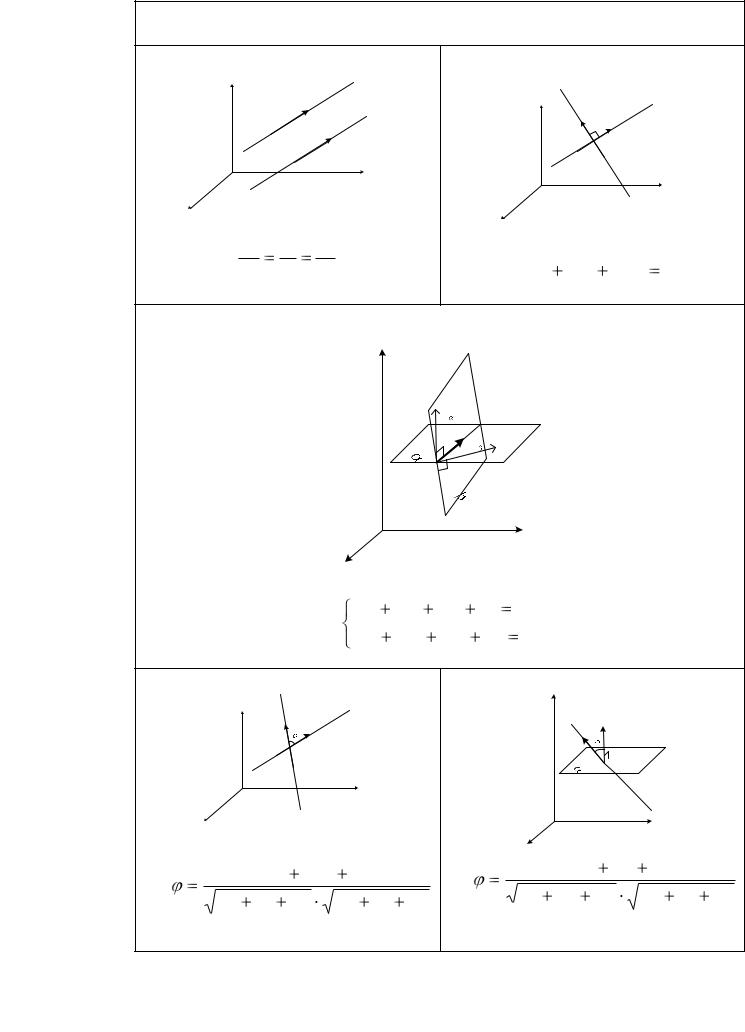
Взаимное расположение прямых l1 и l2 в пространстве:

Условие параллельности прямых:

Условие перпендикулярности прямых:

z

;

2

;

n1

z

;

n1

;

n2

;

m

m

;

(m2

l 1

;

2

y

n2

l

;

l2

l2

(m2

1

y

x

x

m1

n1

p1

m n p

m1m2

n1n2

p1 p2

0

2

2

2

Прямая как линия пересечения плоскостей.

z

n (A1; B1; C1)

l

x

y

A1x B1 y C1 z D1

0;

A2 x B2 y C2 z D2

0.

Угол между двумя прямыми:

Угол между прямой и плоскостью:

z

;

z

n1

)

;

m

p

;

n

;

m

;

2

(

n ( A; B;C)

s

n2

;

(m2

l 1

l

l2

y

x

y

x

m1m2

n1n2

p1 p2

sin

Am

Bn

Cp

cos

A

2

B

2

C

2

m

2

n

2

p

2

2

2

2

2

2

2

m1

n1

p1

m2

n2

p2

38

Образцы решения задач:

ПРИМЕР Составить параметрические уравнения прямой, проходящей через

точку M0 (1; –2; 3) и параллельной вектору s (2; 4; 5) . Найти точку Р прямой, которой соответствует значение t = 2.

x

x0

mt,

РЕШЕНИЕ: Воспользуемся формулами

y

y0

nt,

z

z0

pt.

Так как в данном случае

x0

1, y0

2,

z0

3, m

2, n 4, p 5 , то

параметрические уравнения прямой имеют вид:

x

1

2t,

y

2

4t,

z 3 5t.

При t = 2 получаем

x 1 2 2 5; y

2 4 2 6; z 3 5 2

7.

На прямой фиксирована точка Р (5; 6; –7).

ПРИМЕР Составить канонические уравнения прямой,

проведенной через

точку M0 (6; 2; –3)

и параллельной вектору s (4;

5; 7) . Лежат ли на этой

прямой точки Р (2; 7; –10), Q (10; –3; 5), R (3; 4; 7)?

РЕШЕНИЕ: Применяем формулу

x

x0

y

y0

z

z0

. Так как

m

n

p

x0 6, y0 2, z0

3, m 4, n

5,

p

7 , то канонические уравнения

примут вид

x

6

y

2

z

3

.

4

5

7

Подставляя в эти уравнения координаты точек Р, Q, и R соответственно находим

		2	6		7	2					10		3			1,		10		6		3		2	5		3	,
			4		5						7								4					5			7
								3			6		4			2		7		3	.
											4					5		7
Следовательно, точка Р лежит на прямой, а точки Q, и R на прямой не
лежат.
ПРИМЕР По координатам вершин пирамиды А1А2А3А4 найти:
1)	угол между ребрами А1А2 и													А1А4 ;
2)	площадь грани А А А ;
				1		2		3
																39

3)объем пирамиды;

4)уравнение грани А1А2 А3 ;

5)уравнение высоты, опущенной из вершины А4 ;

6) угол между ребром А А		и гранью А А А .
1	4	1	2	3

А (0; 4; 5) ;	А ( 3; 2; 1) ;	А (4; 5; 6) ;	А (3; 3; 2) .
1	2	3	4

РЕШЕНИЕ:

1.Угол между ребрами А1А2 и А1А4 находим как угол между двумя векторами А1А2 и А1А4 . Для этого требуется знать координаты векторов

А1А2 и А1А4 .Найдем их:

А1А2 = (х2

х1; у2

y ;

z2

z1) =

(3 – 0; 2– 4;

1–5)

=

(3;– 6;

– 4) ;

1

А1А4 = (х

4

х1; у

4

y ;

z4

z1) =

(– 0;

3 – 4; 2 –5)

= (3;

–1;

–3).

1

Косинус угла между двумя векторами

а

(а1; а2 ; а3 )

и

в

(в1; в2 ; в3 )

найдем по формуле

cos

a в

а1в1

а2в2

а3в3

.

а

в

2

2

2

2

2

2

а1

а2

а3

в1

в2

в3

Для данных векторов имеем:

cos

9

6

12

27

.

9

36

16

9

1

9

61

19

Тогда φ = arccos

27

.

61

19

2. Известно, что модуль векторного произведения

а

в равен площади

параллелограмма, построенного на векторах

а ,

в . Тогда площадь

треугольника равна

S

1

a

в

.

2

Рассмотрим векторы А1А2 и

А1А3 :

а = А1А2 = (3; -6; - 4) ; в = А1А3 = (4; 1; 1).

а в = А1А2 х А1А3 =

=	i				j		k				6	4				3 4					3 6
	3			6			4						i						j				k		2i 19 j 27k .
	4			1			1				1	1				4	1				4	1
																				40