Решение систем линейных уравнений

Для решения систем линейных уравнений в MatLAB'е существуют операции '/' и '\'.

Левое деление матриц– '\'.

Ay = b, гдеA– заданная квадратная матрицаNxN, аb– заданный вектор-столбец длиныN. Тогдау = A\b.

Правое деление матриц– '/' – решает систему следующего видаyA = b.

Задание на лабораторную работу

Написать функцию, которая:

1. Вычисляет значение производной в заданной точке. Входные параметры – функция («экспоненциальная», «логарифмическая», «степенная»), координата точки; выходные – значение производной.

2. Вычисляет площадь фигуры, ограниченную полиномом второй степени. Входные параметры – коэффициенты полинома, пределы интегрирования; выходной – площадь.

3. Вычисляет производную полинома второй степени и выводит график исходной функции и производной. Входные параметры – коэффициенты полинома.

4. Находит экстремумы полиномов 3-го порядка. Входные параметры – коэффициенты полинома; выходные – координаты экстремумов.

5. Вычисляет интеграл заданных функций. Входные параметры – функция («экспоненциальная», «логарифмическая», «степенная»), пределы интегрирования; выходные – значение интеграла.

6. Вычисляет скорость и ускорение физического тела в заданной точке. Тело движется по кривой описываемой полиномом третьей степени. Входные параметры – коэффициенты полинома, координата точки; выходные значение скорости и ускорения.

Литература к лабораторной работе №3

1. Мартынов Н.Н. Иванов А.П. MatLAB5.xВычисления. Визуализация. Программирование – М.: КУДИЦ-ОБРАЗ, 2000. – 366 с.

2. Сергиенко А.Б. Цифровая обработка сигналов – СПб.: Питер, 2002. – 608 с.: ил.

Лабораторная работа № 4. Хаотические свойства нелинейных систем Цель работы

Познакомиться с хаотическими свойствами простых нелинейных систем. Исследовать при помощи паутинных диаграмм хаотические свойства нелинейных дискретных отображений.

Введение

Данная лабораторная работа посвящена исследованию явления в нелинейных системах, получившего название детерминированного хаоса¹. Этот вид хаоса порождается не случайным поведением большого количества элементов системы, а внутренней сущностью нелинейных процессов.

Одной из простейших задач, демонстрирующей хаотичность поведения системы является нелинейный рост популяции, описываемый логистическим уравнением

.

На этом примере мы познакомимся с хаотическим поведением нелинейной динамической системы. Независимо от конкретной физической природы любой объект является динамической системой, если можно указать такой набор величин (называемыхдинамическими переменными и характеризующих состояние системы), значения которых в любой последующий момент времени выводятся из начального набора по определенному правилу – закону эволюции.

Дискретные отображения

Рассмотрим функцию, отображающую некоторое множество само с себя:

.

Итерация f ⁽ⁿ⁾функцииfопределяется как композицияf с самой собойnраз:

,.

Итерацию можно выразить другим способом: .

Поскольку каждая точка под действием итераций функцииfперемещается по множествуМ, то функцияfзадает дискретную динамическую систему, т.е. некое движение на множествеМс течением дискретного времениn. Если для некоторой точкиопределены все итерации, то множествоназывается орбитой точкиxпод действием функцииf.

Точка x называется неподвижной точкой функцииf, еслидля любогоn. Неподвижная точкаxфункцииfназывается притягивающей, если все точки из некоторой ее окрестности стремятся кxпод действием итераций функцииf; и отталкивающей, если все точки из некоторой окрестности покидают эту окрестность под действием итераций. Если неподвижная точка является притягивающей либо отталкивающей, то она также называется гиперболической.

Точка xназывается периодической точкой функцииfпериодаk, если, причемприi < k. Орбита периодической точки состоит изkточек и называется циклом периодаk. Точкаxявляется периодической точкой функцииfпериодаk, если она является неподвижной точкой итерации, но не является периодической точкой итераций с меньшими номерами.

Дав основные понятия, можно вернуться к исследованию логистической функции. Исследуемая функция является функцией одного параметра λ. Наша задача выяснить, как меняются орбиты точек, при изменении параметраλ. Чаше всего, при малом изменении параметра динамика, определяемая функцией, меняется мало. Немного изменяются значения неподвижных, периодических точек. Однако при некоторых значениях параметра происходит резкое изменение качественной картины, например, изменяется количество неподвижных точек, меняется их характер (притягивающие превращаются в отталкивающие). Скачкообразное изменение качественного поведения системы при плавном изменении параметра называется бифуркацией.

Рассмотрим, что будет происходить с точками из интервала [0;1] под действием итераций логистической функции.

При 0 < λ< 1 точкаx= 0 является притягивающей, и каждая точка выбранного отрезка под действием итераций стремится к ней. Приλ= 1 происходит бифуркация, и точкаx = 0 перестает быть притягивающей.

При 1 < λ< 3 точкаx= 0 является отталкивающей, а точка– притягивающей неподвижной точкой.

Следующая бифуркация происходит при λ= 3, когда точкаперестает быть притягивающей и превращается в отталкивающую приλ> 3. Поскольку теперь обе точкиx₁иx₂являются отталкивающими, логично предположить о наличии некого притягивающего объекта между ними. Так оно и происходит. Приλ> 3 появляются еще две неподвижные точки, которые не являются неподвижными точками исходной функции. Они образуют цикл периода 2. Таким образом, имеет место бифуркация удвоения периода.

При дальнейшем увеличении параметра λможно наблюдать и дальнейшие бифуркации удвоения периода. Для того чтобы наблюдать весь этот каскад бифуркаций можно провести следующий эксперимент. Выберем какое-либо начальное значениеxи проделаем над ним 100-200 итераций отображения логистической функции. Затем отложим значения следующих 100-200 итераций по вертикальной оси, а значение параметраλ, при котором производились вычисления, – по горизонтальной. По осиλпройдем отрезок от 2,9 до 4 с небольшим интервалом, например 0,01. Полученное множество называется бифуркационной диаграммой логистической функции.

Бифуркационная диаграмма позволяет проследить за развитием системы при плавном изменении параметра. При фиксированном значении параметра за орбитами точек позволяет проследить паутинная диаграмма (диаграмма Ламерея), изображенная на рисунке 1. Построение паутинной диаграммы позволяет выявить различные эффекты, незаметные на бифуркационной.

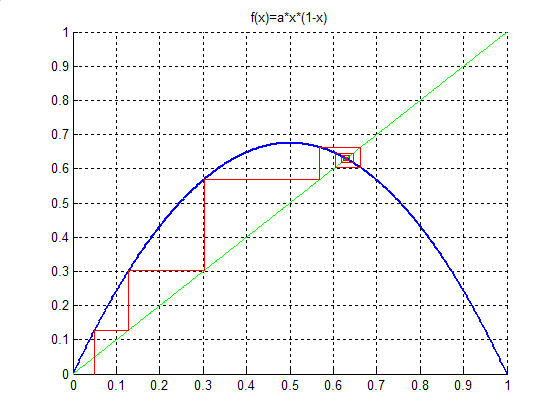
Рис. 4.1. Паутинная диаграмма логистической функции при λ= 2.7