19. Соединение трехфазного источника напряжения и нагрузки треугольником

Рис. 19.1.

Соединение трехфазного источника напряжения и нагрузки треугольником показано на рис. 19.1. Все фазы такой цепи работают независимо друг от друга, так как каждая фаза источника напряжения подключена непосредственно к соответствующей фазе нагрузки.

Токи называются фазными, потому что это токи фаз нагрузки. Токиназываются линейными, так как это токи в линейных проводах.

Напряжения являются одновременно фазными и линейными, так как это напряжения фаз источника и нагрузки, а также напряжения между линейными проводами.

Рассмотрим уравнения, описывающие состояние рассматриваемой цепи. Согласно уравнениям фаз нагрузки (по закону Ома):

По 1-му закону Кирхгофа для узлов цепи:

Для пояснения уравнений построим векторные диаграммы. Рассмотрим некоторые конкретные типы нагрузок.

Простейший случай симметричной резистивной нагрузки показан на рис. 19.2. Из этой диаграммы видно, что для симметричной нагрузки

На рис. 19.3 показана несимметричная резистивная нагрузка - в разных фазах разные резисторы.

На рис. 19.4 изображена диаграмма напряжений и токов несимметричной нагрузки, у которой в фазу abвключен резистор, в фазуbc– активно-индуктивный элемент, в фазуca– активно-емкостной элемент. Главное отличие последнего случая от предыдущих – сдвиги фаз между напряжениями и токами в фазахbcиca.

Рис. 19.2.
Рис. 19.3.
Рис. 19.4.

Активную мощность трехфазной нагрузки при соединении треугольником можно измерить "методом двух ваттметров". Схема измерения показана на рис. 19.5. Общая активная мощность нагрузки равна сумме показаний ваттметров:. Это можно доказать, используя законы Кирхгофа.

По определению

.

С другой стороны,

Здесь использованы выражения линейных токов через фазные, а также равенства ,, последнее из которых представляет собой 2-й закон Кирхгофа для напряжений цепи.

В случае симметричной нагрузки можно измерить мощность только одной фазы и умножить ее на три.

Рис. 19.5.

Тема 3. Дополнительные главы

20. Переходные процессы

Общая теория

Установившимся режимомэлектрической цепи обычно называют режим постоянного тока или режим синусоидального тока. Процесс перехода от одного установившегося режима к другому называютпереходным процессом. Мы будем рассматривать только установившиеся режимы постоянного тока.

Переходные процессы вызываются изменениями конфигурации цепи (переключениями), или резкими изменениями параметров элементов цепи (напряжений и токов источников, сопротивлений резистивных элементов, индуктивностей катушек, емкостей конденсаторов).

Мы будем называть коммутациейлюбое изменение в цепи, приводящее к возникновению переходного процесса. Будем предполагать, что коммутации происходят мгновенно, так как учет их ненулевой длительности требуется только в особых случаях, выходящих за рамки классической теории переходных процессов. Будем считать, что моменту коммутации соответствует начало отсчета времени t= 0.

В общем случае переходные процессы рассчитывают, решая полную систему расчетных уравнений цепи, которая при этом содержит дифференциальные уравнения. Систему составляют и решают для конфигурации цепи после коммутации (для t> 0). Для решения дифференциальных уравнений необходимы начальные условия, заданные в момент непосредственно после коммутацииt= +0.

Независимыми начальными условияминазываются токи катушек и напряжения конденсаторов в момент коммутации. Они определяют энергию, запасенную в катушках и конденсаторах. Все остальные начальные условия называютсязависимымии могут быть рассчитаны по независимым условиям с помощью законов Кирхгофа и уравнений элементов цепи.

Независимые начальные условия рассчитывают для момента времени, непосредственно предшествующего коммутации (t= –0). При этом используют конфигурацию цепи и состояние ее элементов для времени перед коммутацией (дляt< 0). Затем независимые начальные условия переносят на момент времени, непосредственно следующий за коммутацией (t= +0). Это делают с помощью законов коммутации:

1-й закон коммутации -ток в катушке индуктивности невозможно изменить скачком:

i_L(t – 0) = i_L(t + 0)

2-й закон коммутации -напряжение на конденсаторе невозможно изменить скачком:

u_C(t – 0) = u_C(t + 0)

Законы коммутации следуют из уравнений катушки и конденсатора (см. п. 4).

Замечание 1. Систему из п дифференциальных уравнений 1-го порядка можно преобразовать к одному дифференциальному уравнению п-го порядка.

Итак, порядок расчета переходного процесса в общем случае можно представить в виде последовательности действий:

1. Составляют полную систему расчетных уравнений цепи для t> 0. Если это удобно, преобразуют ее к одному дифференциальному уравнению.

2. Составляют полную систему расчетных уравнений цепи для t< 0. Решив ее, получают независимые начальные условия для моментаt= –0.

3. С помощью законов коммутации находят независимые начальные условия для t = +0.

4. Решив систему дифференциальных уравнений (или одно уравнение, если система была к нему преобразована), получают напряжения и токи цепи как функции времени для t> 0.

Переходные процессы в цепях первого порядка

Пример 1. Заряд и разряд и конденсатора через резистор. Соединение резистора и конденсатора называютRC‑цепочкой (рис. 20.1). Подключим ее к источнику, напряжение которого меняется скачком в моментt= 0 (рис. 20.2).

Рис. 20.1. RC-цепочка с источником напряже­ния.

Рис. 20.2. Зависимость напряжения источника от времени.

Запишем полную систему расчетных уравнений цепи рис. 20.1 в виде уравнения единственного контура цепи и уравнений элементов:

,

,.

Подставим выражение для тока из уравнения конденсатора в уравнение резистора, получим . Это выражение подставим в уравнение контура, получим дифференциальное уравнение для напряжения конденсатора:

Рассматривая это уравнение после коммутации (при t> 0), получим:

(20.1)

Чтобы решить это уравнение, к нему надо добавить начальное условие . Чтобы найти его, вначале рассчитаем напряжение на конденсаторе до коммутации. Так как мы предполагаем, что до коммутации (то есть, до моментаt= 0) имел место установившийся режим при постоянных напряжениях, то тока в цепи не было, напряжение на резисторе было равно нулю, и потому напряжение на конденсаторе было равно напряжению источника:. Согласно 2-му закону коммутации,, поэтому искомое начальное условие.

Полное решение уравнения (20.1) найдем в виде

,

где - решение однородного уравнения

, (20.2)

соответствующего уравнению (20.1); - частное решение уравнения (20.1).

Так как правая часть уравнения (20.1) - константа, то ищем также в виде константы. Подстановкав (20.1) дает.

Общее решение однородного уравнения (20.2) имеет вид

, (20.3)

где Аи α - константы. Подстановка (20.3) в (20.2) дает.

Число Аполучим из начального условия. С одной стороны,

.

С другой стороны, , откуда.

Окончательно получаем: .

Показатель экспоненты часто записывают в виде , где в данном случае τ =RC:

.

Графики напряжения на конденсаторе для случая R= 20 Ом,С= 100 мкФ представлены на рис. 20.3, 20.4.

Знаменатель в показателе экспоненты τ называется постоянной временипереходного процесса. Проводя касательные к графику экспоненты, на их пересечении с горизонтальной прямой, соответствующей установившемуся решению после коммутации, можно получить отметки, отсекающие отрезки длиной τ (рис. 20.3, 20.4). В нашем случае τ =RC= 20·100·10^-6= 0,002 с.

За время 3–5 τ переходной процесс практически полностью заканчивается: ;. Время 3–5 τ приближенно считают длительностью переходного процесса.

Рис. 20.3. Заряд конденсатора через резистор. V1 = 40 B, V2 = 200 B.

Рис. 20.4. Разряд конденсатора через резистор. V1 = 160 B, V2 = 0 B.

Замечание 2. В электротехнике частное решение дифференциального уравнения часто называют принужденной составляющей переходного процесса, а решение соответствующего однородного уравнения - свободной составляющей переходного процесса.

Рис. 20.5. Схема цепи с катушкой.

Рис. 20.6. Эквивалентная схема цепи с катушкой.

Пример 2. Изменение тока в катушке индуктивности при переключениях в цепи с источником постоянного напряжения (рис. 20.5).

Заменим резисторы R₁иR₂с ключомSA₁одним резисторомR(рис. 20.6), сопротивление которого скачком меняется в моментt= 0 в зависимости от состояния ключа:при замкнутом ключе,при разомкнутом ключе. Обозначим.

Вначале выведем уравнение для тока катушки и получим для него начальное условие в общем виде, затем отдельно рассмотрим случаи замыкания и размыкания ключа.

Запишем полную систему уравнений цепи:

уравнение единственного контура цепи: ,

уравнения элементов: ,,.

Подставив уравнения элементов в уравнение контура и разделив это уравнение на R, получим уравнение переходного процесса (для напряжения источника сохраним обозначениеu, чтобы не путать ЭДС с экспонентой):

, (20.4)

причем здесь имеется в виду значение Rпосле коммутации (так как переходной процесс протекает после коммутации).

Перед коммутацией в цепи был установившийся режим постоянного тока. Поэтому напряжение на катушке было равно нулю, значит, . Заметим, что сюда нужно подставить значениеRдо коммутации (так как начальные условия определяются состоянием цепи до коммутации). Далее, по 1-му закону коммутации, поэтому.

Рассмотрим случай, когда в момент t= 0 ключ замыкается, то естьдо коммутации ипосле коммутации. Уравнение (20.4) и начальное условие для тока катушки будут иметь вид:

Рис. 20.7. Нарастание тока в катушке

при уменьшении сопротивления.

Рис. 20.8. Напряжение катушки при нарастании тока.

,.

Решением задачи будет функция , где- постоянная времени переходного процесса.

Графики тока и напряжения катушки для значений R₁= 10 Ом,R₂= 90 Ом (при этомR₁₂= 9 Ом),L = 0,02 Гн,е= 9 В показаны на рис. 20.7, 20.8. Здесь мы не будем подробно разбирать решение дифференциального уравнения, так как это уже сделано в предыдущем примере, и кроме того, это изучается в курсе математики.

Теперь рассмотрим случай, когда в момент t = 0 ключ размыкается, то естьдо коммутации ипосле коммутации. Уравнение (20.4) и начальное условие для тока катушки примут вид:

,.

Рис. 20.9. Затухание тока катушки

при увеличении сопротивления.

Рис. 20.10. Напряжение катушки при затухании тока.

Решением задачи будет функция, где- постоянная времени переходного процесса. Графики тока и напряжения катушки показаны на рис. 20.9, 20.10. Значения параметров те же, что и в случае замыкания ключа.

Обратите внимание на то, что масштаб времени на рис. 20.7, 20.8 и рис. 20.9, 20.10 отличается в 10 раз. Затухание тока при размыкании ключа в рассматриваемой цепи происходит в 10 раз быстрее, чем нарастание тока при замыкании ключа, так как постоянная времени при замыкании в 10 раз больше (потому что).

Масштабы напряжения на рис. 20.8 и рис. 20.10 также отличаются в 10 раз. Особо нужно отметить, что при быстром уменьшении тока в катушке напряжение на ней по абсолютной величине во много раз больше напряжения источника, создавшего этот ток. Это свойство катушки часто используется для получения импульсов высокого напряжения. Например, на этом эффекте основана работа автомобильных систем зажигания.

Переходные процессы в цепях второго порядка

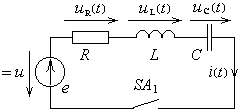
Рис. 20.11. Подключение после-

довательного соединения R,L,C к

источнику постоянного напряжения.

Пример 3. Подключение последовательного соединения резистора, катушки и конденсатора к источнику постоянного напряжения (рис. 20.11).

Запишем полную систему расчетных уравнений цепи:

уравнение контура ,

уравнения элементов ,,,.

Подставляя выражение для тока из уравнения конденсатора в уравнения катушки и резистора, получим:

, .

Подставим выражения для напряжений элементов в уравнение контура, получим дифференциальное уравнение переходного процесса для напряжения конденсатора:

. (20.5)

Для уравнения второго порядка нужны два начальных условия: и. При разомкнутом ключе начальное напряжение на конденсаторе может быть любым. Положим. По 2-му закону коммутации, поэтому. До коммутации тока в цепи не было:. Так как единственная ветвь цепи содержит катушку, то по первому закону коммутации, значит,. Согласно уравнению конденсатора,, поэтому.

Решение представим в виде суммы:, где- частное решение уравнения (20.5). Это решение ищем в виде константы, что при подстановке в (20.5) дает.

Функция - это решение соответствующего однородного уравнения

.

Она имеет вид

при, (20.6)

при. (20.7)

где α₁и α₂- корни характеристического уравнения:

,, здесь, . (20.8)

Рассмотрим отдельно три случая:

1. -апериодический процесс. При этом,- действительные числа,. График напряжениядляR= 20 Ом,L= 10 мГн,C= 200 мкФ,е= 200 В показан на рис. 20.12.

Рис. 20.12. Апериодический переходной процесс.

Рассчитаем значения коэффициентов α₁и α₂по формулам 20.8:

Гц,рад/с,

Гц,Гц.

Подставим полученные коэффициенты в формулу (20.6) и потребуем выполнения начальных условий, учитывая, что ,,то есть,:, следовательно,

. (20.9)

, следовательно, дифференцируя выражение дляи приравнивая производную к нулю в момент t= 0, получим:

.(20.10)

Решив совместно уравнения (20.9) и (20.20), получим: A₁= -241,6 В,А₂= 41,6 В.

Окончательно,

В.

2. -критический процесс, пограничный между апериодическим и колебательным. При этом,, процесс затухает за минимальное время. График напряжениядляR = 20 Ом,L = 10 мГн,C= 100 мкФ,е= 200 В показан на рис. 20.13.

Рис. 20.13. Критический переходной процесс.

Найдем коэффициенты А₁иА₂в выражении для. В данном случае , с учетом формулы (20.7),. Как и в случае периодического режима, потребуем выполнения начальных условий:

, следовательно,,.

, следовательно, дифференцируя выражение дляи приравнивая производную к нулю в момент t= 0, получим:

,.

Окончательно получим:

.

3. - колебательный режим. При этом,- пара сопряженных комплексных чисел. В этом случае решение однородного уравненияудобно представить в виде

, (20.11)

здесь - частота собственных колебаний (см. п. 15).

Тогда полное решение уравнения 20.5 будет выражаться формулой

. (20.12)

Рис. 20.14. Колебательный переходной процесс.

График этого напряжения дляR = 20 Ом,L = 10 мГн,C= 2 мкФ,е= 200 В показан на рис. 20.14. Вычислим для этого набора исходных данных все коэффициенты в выражении (20.11). Как и в предыдущих случаях,Гц,В.

Далее, по формулам 20.8 и 20.11 получим:

рад/с,рад/с.

Рассчитаем коэффициенты А₁иА₂, исходя из начальных условий.

, следовательно,,В.

, следовательно, дифференцируя выражение дляи приравнивая производную к нулю в момент t = 0, получим:, то есть,,В.

Окончательно: В.

Замечание 3. Мы рассчитывали только одну величину для каждой задачи: напряжение конденсатора в 1 и 3 примерах и ток катушки во 2 примере. Все остальные напряжения и токи (например, напряжение катушки в примере 2) могут быть получены по результатам таких расчетов с помощью уравнений элементов и законов Кирхгофа.

Замечание 4. В настоящее время для расчета любых режимов электрических цепей обычно применяют численные алгоритмы, реализованные в виде различных компьютерных программ. Это очень удобно для практических расчетов, однако, инженеру нужно понимать теоретическую основу расчетов и знать особенности аналитических решений. Кроме того, надо иметь в виду, что компьютерные программы иногда выдают ошибочные решения, поэтому их нужно уметь каким-то способом контролировать.