
- •II. Пределы и непрерывность
- •§ 4. Пределы функций
- •Предел дробно-рациональной функции в точке
- •Пределы дробно-рациональных функций с квадратичными выражениями
- •Предел дробно-рациональной функции в бесконечности
- •Пределы иррациональных функций
- •Примеры сопряжённых выражений
- •Тригонометрические пределы. Первый замечательный предел
- •Второй замечательный предел
- •§ 5. Непрерывность функций
- •Исследование кусочно-заданных функций на непрерывность
- •Непрерывность дробно-рациональных функций
- •Непрерывность некоторых сложных функций
Пределы дробно-рациональных функций с квадратичными выражениями
В случае
неопределённости
![]() следует разложить квадратичное выражение
на множители. Для этого можно
следует разложить квадратичное выражение
на множители. Для этого можно
а)
воспользоваться тождеством
![]() ,
где
,
где![]() и
и![]() – корни уравнения
– корни уравнения![]() ,
найденные по формуле
,
найденные по формуле![]() ;
;
б)
учесть, что, когда
![]() ,
то
,
то![]() – один из корней, и другой корень
– один из корней, и другой корень![]() можно найти по теореме Виета, например,
из равенства
можно найти по теореме Виета, например,
из равенства![]() ,
где
,
где![]() ;
;
в)
применить равенство
![]() ,
где
,
где
![]() .
.
Пример 7.
![]()
![]()
(решили уравнения
![]() и
и![]() и применили 1-й способ).
и применили 1-й способ).
Пример 8.
![]()
![]() .
.
В уравнении
![]() свободный коэффициент –10 разделили на
коэффициент, стоящий перед
свободный коэффициент –10 разделили на
коэффициент, стоящий перед![]() (число 4). Результат разделили на известный
корень 2. Получили 2-й корень
(число 4). Результат разделили на известный
корень 2. Получили 2-й корень![]() .
.
Затем в уравнении
![]() нашли 2-й корень из условия
нашли 2-й корень из условия![]() ,
где 2 – известный корень, а 6 – свободный
коэффициент (Теорема Виета).
,
где 2 – известный корень, а 6 – свободный
коэффициент (Теорема Виета).
Пример 9.
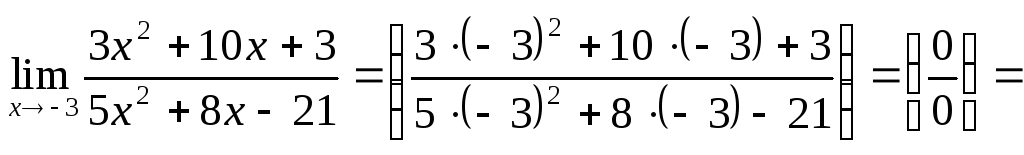
![]() .
.
Скобка
![]() получена как
получена как![]() ,
а остальные найдены 3-м способом.
,
а остальные найдены 3-м способом.
ПР6. Раскройте
неопределённость
![]() ,
разложив дробь на множители:
,
разложив дробь на множители:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
г)
;
г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
г)
;
г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
г)
;
г)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
г)
;
г)![]() .
.
Пример 10.
![]()
![]() .
.
Предел дробно-рациональной функции в бесконечности
Пусть дана функция
![]() (см. стр. 16) и надо найти
(см. стр. 16) и надо найти![]() .
Оказывается, при
.
Оказывается, при![]() вся дробь ведёт себя так, как отношение
старших степеней:
вся дробь ведёт себя так, как отношение
старших степеней:
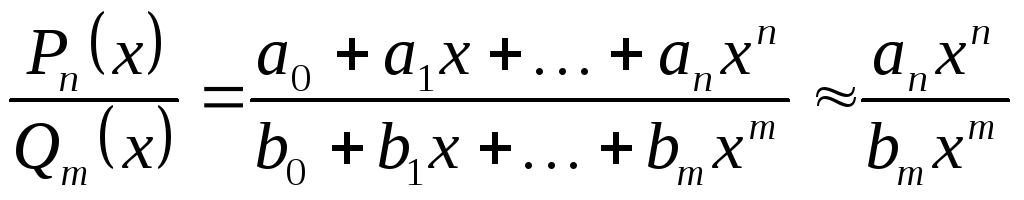 .
.
Тогда
 .
Обозначим
.
Обозначим![]() .
Возможны 3 случая:
.
Возможны 3 случая:
1)
![]() ,
тогда
,
тогда![]() ,
где
,
где
![]() (
(![]() );
);
2)
![]() ,
тогда
,
тогда![]() ,
где
,
где
![]() (
(![]() );
);
3)
![]() ,
тогда
,
тогда![]() .
.
Таким образом, предел равен
а) бесконечности, если степень числителя больше, чем степень знаменателя;
б) 0 в противоположном случае;
в) отношению старших коэффициентов, если степени равны.
ПР7. Найдите пределы
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
д)
;
д)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
д)
;
д)![]() ;
;
ПР8. Найдите пределы
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() .
.
Пример 11. Оставив в числителе и в знаменателе старшие степени, находим
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Пример 12. Оставив старшие степени, видим, что
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Обратите внимание, что знак бесконечности (если таковая получается) в ответе не указывается. Тем не менее, если обе старшие степени – чётные (или если обе нечётные), очевидно, их отношение всегда положительно, что можно учесть.
ПР9. Найдите
пределы функций
![]() в точках
в точках![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
а также при
,
а также при![]() .
.
![]() .
.
Пределы иррациональных функций
Если функция
содержит корень, подставляем, как обычно,
предельную точку. Сложности связаны с
неопределённостью
![]() ,
когда приходится умножать числитель и
знаменатель насопряжённое
выражение.
,
когда приходится умножать числитель и
знаменатель насопряжённое
выражение.
Выражения сопряжены
относительно
разности квадратов,
если их произведение превращается в
разность квадратов по формуле
![]() .
.
Примеры сопряжённых выражений
а)
![]() сопряжено с
сопряжено с![]() ,
при этом
,
при этом![]() ;
;
б)
![]() сопряжено с
сопряжено с![]() ,
и тогда
,
и тогда![]() ;
;
в)
![]() сопряжено с
сопряжено с![]() ,
поскольку
,
поскольку
![]() ,
,
причём под корнем всё остаётся без изменений;
г)
![]() сопряжено с
сопряжено с![]() :
:
![]() .
.
ПР10. Найдите пределы иррациональных функций простой подстановкой:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() .
.
Пример 13. Подставив указанные точки, находим значения
а)
![]() ;
;
б)
![]() .
.
ПР11. Раскройте
неопределённость
![]() ,
умножив числитель и знаменатель дроби
на подходящее сопряжённое выражение и
сократив одинаковые скобки:
,
умножив числитель и знаменатель дроби
на подходящее сопряжённое выражение и
сократив одинаковые скобки:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() ; д)
; д)![]() ; е)
; е)![]() .
.
Пример 14.
![]()
![]() .
.
Пример 15.
![]()
![]()
![]() .
.
Пример 16.
![]()
![]()
![]()
![]() .
.
ПР12. Умножьте
числитель и знаменатель на выражение,
сопряжённое к числителю, а затем – на
выражение, сопряжённое к знаменателю.
Сократив скобки, раскройте неопределённость
![]() :
:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)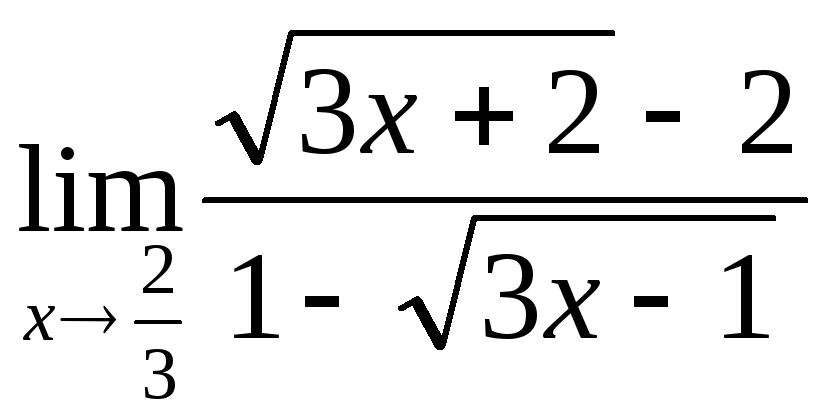 ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() .
.
Пример 17. Умножим, чтобы получить разность квадратов:
![]()
![]()
![]() .
.
Пример 18. Так же, как в примере 17,
![]()
![]()
![]()
![]()
![]()
![]() .
.
Иррациональные
пределы при
![]() в случае неопределённости
в случае неопределённости![]() находят подобно рациональным, при помощи
старших степеней, а в случае неопределённости
находят подобно рациональным, при помощи
старших степеней, а в случае неопределённости![]() сводят её к
сводят её к![]() при помощи сопряжённого выражения.
при помощи сопряжённого выражения.
