
- •II. Пределы и непрерывность
- •§ 4. Пределы функций
- •Предел дробно-рациональной функции в точке
- •Пределы дробно-рациональных функций с квадратичными выражениями
- •Предел дробно-рациональной функции в бесконечности
- •Пределы иррациональных функций
- •Примеры сопряжённых выражений
- •Тригонометрические пределы. Первый замечательный предел
- •Второй замечательный предел
- •§ 5. Непрерывность функций
- •Исследование кусочно-заданных функций на непрерывность
- •Непрерывность дробно-рациональных функций
- •Непрерывность некоторых сложных функций
Непрерывность некоторых сложных функций
Здесь даны примеры
исследования на непрерывность функций
![]() ,
где
,
где![]() – некоторая разрывная функция. Основная
трудность вызвана тем, что значение
величины
– некоторая разрывная функция. Основная
трудность вызвана тем, что значение
величины![]() зависит от знака бесконечности и от
того, будет ли
зависит от знака бесконечности и от
того, будет ли![]() .
.
Пример 15.
Найдём точку разрыва функции
![]() и проверим поведение функции вблизи
этой точки.
и проверим поведение функции вблизи
этой точки.
Поскольку число
2 можно возвести в любую степень, смотрим,
при любых ли значениях x
существует сам показатель степень. Нет,
число
![]() подставить нельзя – получится деление
на 0. Значит, надо найти предел в точке
подставить нельзя – получится деление
на 0. Значит, надо найти предел в точке![]() :
:
![]() .
.
Но результат
зависит от знака бесконечности. Основание
![]() ,
а функция
,
а функция![]() возрастает на всей числовой оси, принимая
значения от 0 до
возрастает на всей числовой оси, принимая
значения от 0 до![]() .
Значит,
.
Значит,![]() ,
а
,
а![]() .
.
В свою очередь
знак бесконечности зависит от того, с
какой стороны подойти к точке
![]() .
Поэтому находим пределы слева и справа:
.
Поэтому находим пределы слева и справа:
а)
![]() ;
;
б)
![]() .
.
Итак, предел слева
равен 0, предел справа равен
![]() .
Когда хотя бы с одной стороны предел
бесконечен, получается разрыв 2-го рода
(бесконечный
скачок).
.
Когда хотя бы с одной стороны предел
бесконечен, получается разрыв 2-го рода
(бесконечный
скачок).
Ответ:
разрыв 2-го рода в точке
![]() ,
предел слева 0, справа
,
предел слева 0, справа![]() .
.
Замечание 4. Далее в заданиях показатель степени в скобки не берём.
Пример 16.
Исследуем на непрерывность функцию
![]() .
.
Знаменатель не
должен обращаться в 0. Но
![]() ,
если
,
если![]() .
Находим пределы слева и справа в точке
.
Находим пределы слева и справа в точке![]() .
Учтём, что основание
.
Учтём, что основание![]() ,
и потому функция
,
и потому функция![]() убывает от
убывает от![]() до 0, а именно,
до 0, а именно,![]() и
и![]() .
.
а)
![]() ;
;
б)
![]()
(при раскрытии
скобок
![]() ,
но знак 0 меняется на противоположный).
,
но знак 0 меняется на противоположный).
Ответ:
разрыв 2-го рода в точке
![]() ;
предел слева равен
;
предел слева равен![]() ,
справа – 0.
,
справа – 0.
Пример 17.
Найти точки разрыва функции
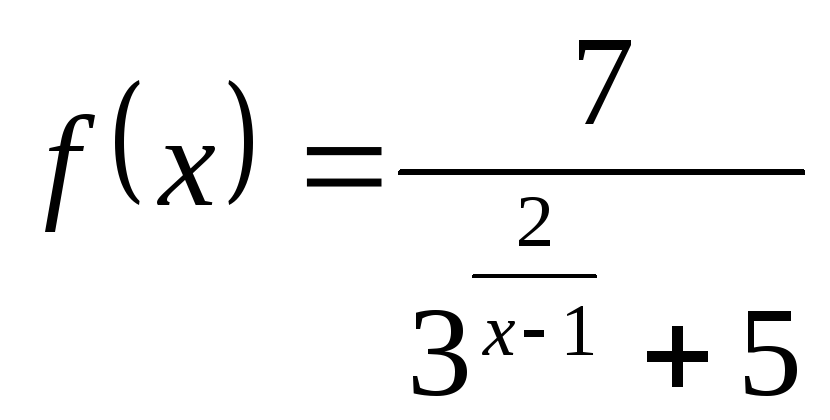 ,
определить их тип.
,
определить их тип.
Очевидно, большой
знаменатель не должен обращаться в 0.
Но показательная функция
![]() всегда положительна, тем более – если
прибавить к ней 5.
всегда положительна, тем более – если
прибавить к ней 5.
Значит, проблемы
могут возникнуть только со знаменателем
![]() .
Действительно, число
.
Действительно, число![]() подставить нельзя – возникает деление
на 0.
подставить нельзя – возникает деление
на 0.
Воспользуемся
методом близкой точки, взяв в качестве
![]() и
и![]() соответственно 0,999 и 1,001.
соответственно 0,999 и 1,001.
Пусть
![]() .
Тогда
.
Тогда
а)
![]() ; б)
; б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() .
.
Пусть теперь
![]() .
Тогда
.
Тогда
а)
![]() ; б)
; б)![]() ;
в)
;
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() .
.
Тем самым предел
слева равен 1,4, а предел справа равен 0.
Значит, в точке
![]() получается разрыв 1-го рода – конечный
скачок от значения 1,4 до значения 0.
получается разрыв 1-го рода – конечный
скачок от значения 1,4 до значения 0.
Ответ:
разрыв 1-го рода в точке
![]() ,
предел слева равен 1,4, справа – 0.
,
предел слева равен 1,4, справа – 0.
Пример 18
(повышенной сложности).
Исследуем на непрерывность функцию
 ,
найдём точки разрыва, определим их тип.
,
найдём точки разрыва, определим их тип.
Возможны два проблемных случая:
а) в 0 обращается
знаменатель
![]() (очевидно, когда
(очевидно, когда![]() );
);
б) в 0 обращается
знаменатель всей дроби (когда
![]() ).
).
Эти случаи рассматриваются отдельно и независимо один от другого.
1-й случай.
Пусть
![]() .
Найдём пределы слева и справа тем же
способом, что в примере 17.
.
Найдём пределы слева и справа тем же
способом, что в примере 17.
В качестве числа
![]() возьмём
возьмём![]() .
Тогда
.
Тогда
а)
![]() ; б)
; б)![]() в)
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
Предел слева в точке 3 равен 0.
В качестве числа
![]() возьмём
возьмём![]() .
Тогда
.
Тогда
а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() .
.
Предел справа в точке 3 равен –48.
В точке
![]() имеет место разрыв 1-го рода – конечный
скачок от значения 0 до значения –48.
имеет место разрыв 1-го рода – конечный
скачок от значения 0 до значения –48.
2-й случай.
Пусть
![]() ,
или, что то же самое,
,
или, что то же самое,![]() (учтём, что
(учтём, что![]() ).
Тогда
).
Тогда![]() ,
поскольку функция
,
поскольку функция![]() монотонна.
монотонна.
Значит,
![]() ,
откуда
,
откуда![]() ,
и
,
и![]() – точка разрыва. Поскольку в ней
получается
– точка разрыва. Поскольку в ней
получается![]() ,
разрыв будет 2-го рода.
,
разрыв будет 2-го рода.
Выясним знак
бесконечности, если подходить слева и
справа к точке
![]() .
.
Поскольку
![]() ,
в качестве
,
в качестве![]() возьмём
возьмём![]() ,
а в качестве
,
а в качестве![]() возьмём
возьмём![]() .
.
Пусть
![]() ,
тогда
,
тогда
а)
![]() ; б)
; б)![]() в)
в)![]() ;
;
г)
![]() ;
д) знаменатель
;
д) знаменатель![]() ;
е)
;
е)![]() .
.
Предел слева в
точке
![]() равен
равен![]() .
.
Пусть
![]() ,
тогда
,
тогда
а)
![]() ; б)
; б)![]() в)
в)![]() ;
;
г)
![]() ;
д) знаменатель
;
д) знаменатель![]() ;
е)
;
е)![]() .
.
Итак, если подходить
к
![]() слева, функция стремится к
слева, функция стремится к![]() ,
а если подходить справа – стремится к
,
а если подходить справа – стремится к![]() .
.
Ответ:
Функция терпит неустранимый разрыв
1-го рода в точке
![]() ,
при этом предел слева равен 0, а предел
справа равен
,
при этом предел слева равен 0, а предел
справа равен![]() .
Кроме того, функция терпит разрыв 2-го
рода в точке
.
Кроме того, функция терпит разрыв 2-го
рода в точке![]() ,
при этом предел слева равен
,
при этом предел слева равен![]() ,
а предел справа равен
,
а предел справа равен![]() .
.
Пример 19. Исследуем
на непрерывность функцию
![]() .
.
Понятно, что
![]() – точка разрыва. Но если
– точка разрыва. Но если![]() ,
то всегда
,
то всегда![]() .
.
Тогда
![]() ,
и степень положительна при любом
аргументе, в том числе при
,
и степень положительна при любом
аргументе, в том числе при![]() .
Но при
.
Но при![]() степень бесконечна, и получается
степень бесконечна, и получается![]() ,
или
,
или![]() .
.
Ответ:
разрыв 2-го рода в точке
![]() ,
пределы и слева, и справа равны
,
пределы и слева, и справа равны![]() .
.
Замечание 5. Совпадение знака бесконечности ни в коем случае не означает, что перед нами – точка устранимого разрыва. Разрыв устраним только для конечных числовых значений (когда совпадают числа).
Пример 20. Проверим
непрерывность функции
![]() .
Непрерывность нарушается, если
.
Непрерывность нарушается, если![]() ,
или
,
или![]() .
.
Пусть
![]() :
:
а)
![]() ;
;
б)
![]() .
.
Пусть
![]() :
:
а)
![]() .
.
б)
![]() ;
;
Ответ:
разрыв 2-го рода в точках
![]() и
и![]() .
В 1-й точке предел слева равен
.
В 1-й точке предел слева равен![]() ,
предел справа равен 0; во 2-й точке – всё
наоборот.
,
предел справа равен 0; во 2-й точке – всё
наоборот.
НФ11. Исследуйте функции на непрерывность, покажите схематично их поведение вблизи точек разрыва:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() .
.
НФ12. Задание то же, что в НФ11:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
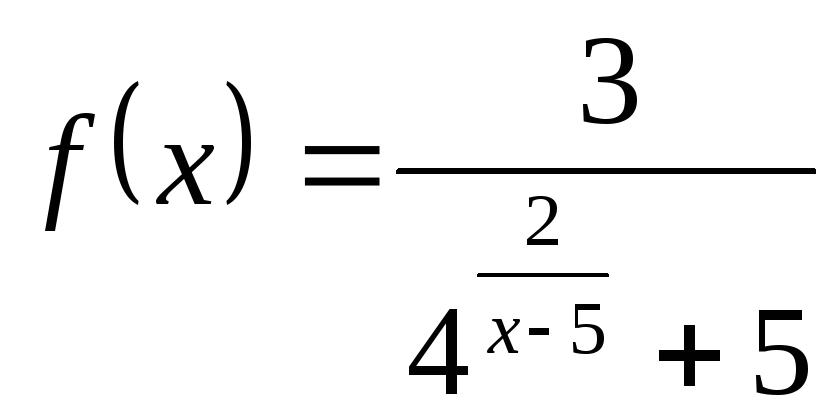 ; б)
; б)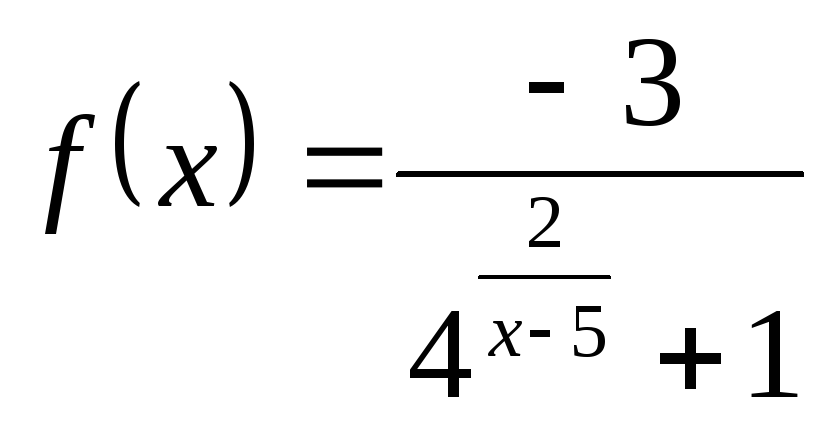 ; в)
; в)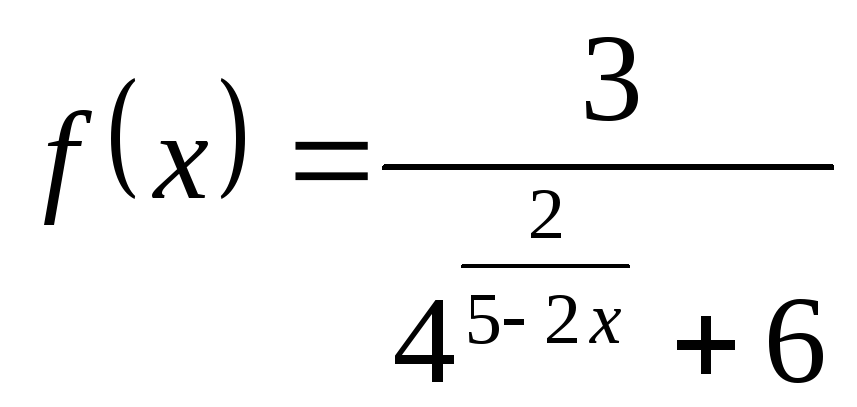 ; г)
; г)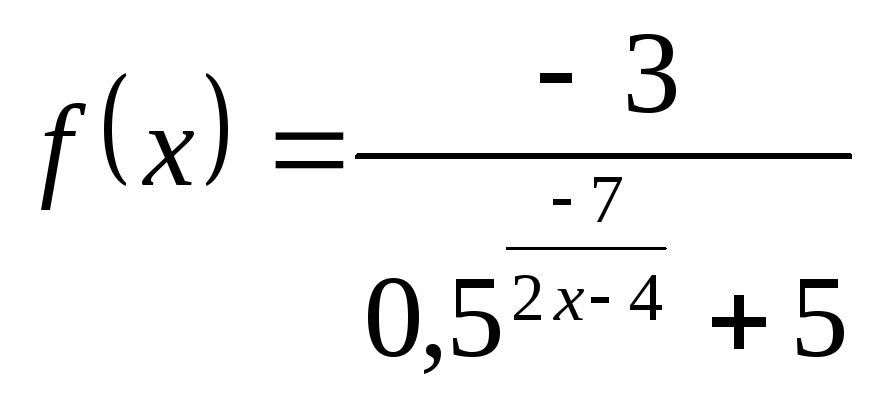 ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
4) а)
 ; б)
; б) ; в)
; в)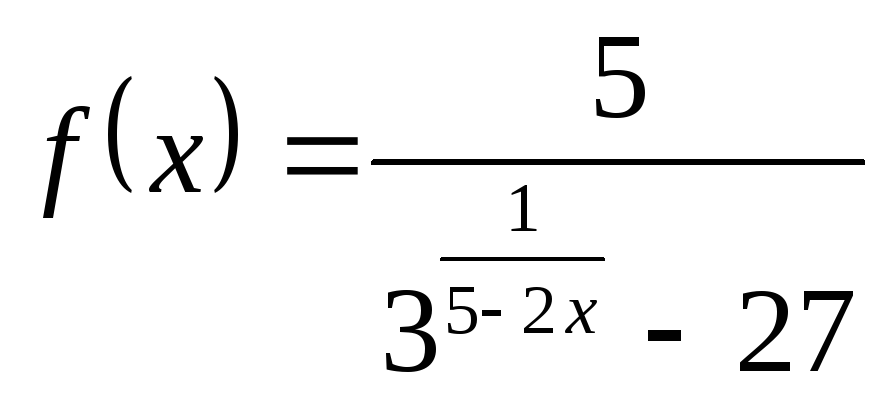 ; г)
; г)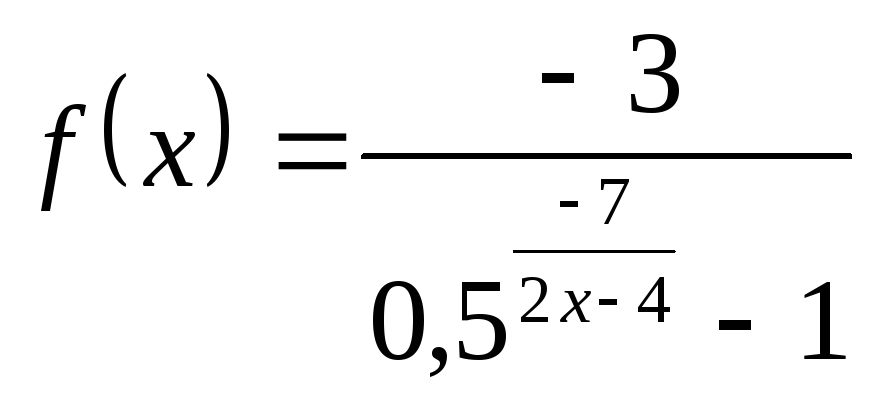 .
.
НФ13. Задание то же, что в НФ11:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() .
.
Пример 21.
Пусть предложено выяснить, как функция
![]() ведёт себя в точках разрыва.
ведёт себя в точках разрыва.
Распространённая
ошибка – решая уравнение
![]() и считая, что точки разрыва обязаны
быть, раз о них речь в условии, взять
и считая, что точки разрыва обязаны
быть, раз о них речь в условии, взять![]() .
На самом деле
.
На самом деле
а) уравнение
![]() корней не имеет;
корней не имеет;
б) соответственно
знаменатель дроби
![]() в 0 не обращается;
в 0 не обращается;
в) поэтому дробь определена при любых значениях x;
г) тогда, поскольку 3 можно возвести в любую степень, вся функция также определена при любых значениях x.
Никаких точек разрыва нет, функция непрерывна на всей числовой оси.
Пример 22.
Исследуем на непрерывность функцию
![]() .
.
Функция
![]() определена на отрезке
определена на отрезке![]() .
Значит, должно быть выполнено неравенство
.
Значит, должно быть выполнено неравенство![]() ,
или
,
или![]() .
При этом
.
При этом
а) неравенство
![]() выполнено при любом действительномx;
выполнено при любом действительномx;
б) неравенство
![]() выполнено только при
выполнено только при![]() .
.
Тем самым вся
функция
![]() определена в единственной точке
определена в единственной точке![]() .
Пределы слева и справа не имеют смысла.
.
Пределы слева и справа не имеют смысла.
Пример 23.
Исследуем на непрерывность функцию
![]() .
.
Должно выполняться
неравенство
![]() или, что равносильно,
или, что равносильно,![]() .
При этом
.
При этом
а) неравенство
![]() выполнено при любом действительномx;
выполнено при любом действительномx;
б) неравенство
![]() выполнено только при
выполнено только при![]() .
.
Поскольку
![]() и
и![]() не определены, в 1-й точке функция
непрерывна справа, а во 2-й – слева. На
интервале
не определены, в 1-й точке функция
непрерывна справа, а во 2-й – слева. На
интервале![]() функция непрерывна.
функция непрерывна.
