Ременные передачи в отличие от зубчатых передач работают бесшумно, на высоких скоростях; способны передавать движение на сравнительно большие (до 15 м) расстояния; при перегрузках ремень (ремни) проскальзывает по шкивам – передача не повреждается.

Вместе с этим, размеры шкивов намного превышают размеры зубчатых колес; предварительное натяжение ремня (ремней) намного (в 2-3 раза) увеличивает нагрузку на подшипники; передаточное число оказывается зависимым от нагрузки (не постоянно).

Наиболее распространена клиноременная передача – обычно с несколькими клиновыми ремнями. На рисунке 20.2 показаны фрагменты ремней, расположенные за шкивом передачи. На рисунке 20.3 показана плоскоременная передача – с одним плоским ремнем.

Рисунок 20.2 – Клиновые ремни

Рисунок 20.3 – Плоский ремень

20.1 Кинематика ременной передачи

Если считать, что ремень не проскальзывает по шкивам, скорость его (в первом приближении) равна окружным скоростям шкивов:

V	=ω	D1 =V			=ω		D2	=V ,	(20.1)
1	1	2				2	2	2
передаточное отношение			ω1		D2
	i =			=		=u.			(20.2)
			ω2		D1

Но скольжение ремня по шкивам неизбежно.

Действительно, ведущая ветвь ремня (рис. 20.4) натянута сильнее ведомой. По мере огибания ведущего шкива натяжение ремня ослабевает, упругое удлинение ремня становится меньше – ремень “съеживается”, скользя по ремню. Это скольжение называется упругим. Из-за него ремень отстает от ведущего шкива, но обгоняет ведомый; скорости (20.1) не равны:

V1 =ω1 D21 >V >ω2 D22 =V2 ,

передаточное отношение (20.2)

134

i =	ω1		>	D2	=u,
	ω	2		D
				1	(20.3)
i =			D2
					,
	D		(1	−ε)
		1

где ε ≈ 0, 01…0,02 – коэффициент упругого скольжения. При этих значениях коэффициента ε отношение (20.3), практически, не отличается от числа (20.2).

20.2 Геометрия ременной передачи

Синус угла наклона ведущей ветви ремня к горизонту находится из рассмотрения О1О2С (рис. 20.4):

sin β = О2С = D2 − D1 , 2 ОО1 2 2a

или (при обычно небольших углах β)

β ≈ D2 a− D1 = D1 u a−1,

что дает угол обхвата ведущего шкива

α°=180°− β ≈180°−

D1 (u −1) 57°,

(20.4)

a

a – межосевое расстояние, u – передаточное число (20.2).

Длина ремня

D1

β) D2

L = 2acos β

+ (π

− β)

+

(π +

,

где

2

2

2

2

β

1

2 β

1

β

cos

= 1−sin

2 β

≈1−

sin

≈1−

2

2

2

2

2

2

;

приближенно

L ≈ 2a +

π

(D

+ D )

+

(D − D )2

(20.5)

2

1 .

2

1

2

4a

Рисунок 20.4 – К определению угла обхвата и длины ремня

135

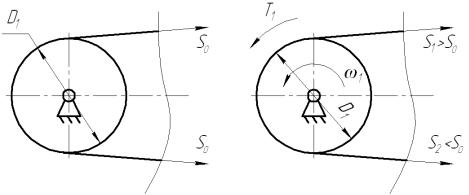
20.3 Силы в передаче

На рисунке 20.5 показан ведущий шкив неработающей передачи (ветви ремня натянуты силами предварительного натяжения S0) и работающей передачи (ведущая ветвь натянута сильнее ведомой: S1 > S2). Понятно, что н атяжение ведущей ветви S1 > S0, или

S1 = S0 + S;

(20.6)

ведущая ветвь получает дополнительное удлинение, что компенсируется таким же по величине дополнительным укорочением ведомой ветви (так как длина ремня задана, она одна и та же в неработающей и работающей передаче):

S2 = S0 - S.

(20.7)

Сумма натяжений (20.6–20.7) ветвей ремня

S1 + S2 = 2S0. (20.8)

Ведущий шкив работающей передачи вращается равномерно – сумма моментов сил, действующих на него, равна 0:

S	D1 − S		D2	−T = 0,
1	2	2	2	1
разность натяжений	S1 - S2 = 2Т1 / D1				(20.9)
равна окружной силе, или полезной нагрузке

Ft = 2T1 .

D1

Рисунок 20.5 – Неработающая и работающая передачи: S0 – силы предварительного натяжения, S1 и S2 – натяжения ветвей ремня

20.4 Формула Эйлера

Уравнения (20.8) и (20.9) требуется дополнить связью между натяжениями S1 и S2. Рассмотрим (с целью найти эту связь) равновесие бесконечно короткого фрагмента ремня на ведущем шкиве (рис. 20.6). Уравнения равновесия (в проекциях на касательную t и нормаль n к поверхности шкива):

136

	−S cos dϕ	+ (S + dS)cos dϕ		− fdN = 0,
	2		2		(20.10)
	dN − S sin dϕ		−(S + dS)sin dϕ
					= 0.
		2		2

Рисунок 20.6 – К выводу формулы Эйлера

В уравнения (20.10) входят натяжения в сечениях, ограничивающих фрагмент ремня, нормальная реакция dN поверхности шкива и сила трения, определяемая законом Амонтона

dFтр = fdN,

	f – коэффициент трения.
	Пределы
	cos dϕ				= lim cos					∆ϕ	= cos0 =1,
	2					∆ϕ→0				2
		sin dϕ						sin		∆ϕ
		2			= lim					2	=1,
		dϕ							∆ϕ
						∆ϕ→0
	2		dϕ				dϕ		2
	что позволяет заменить sin					на			; бесконечно малую dSdφ второго порядка
	2				2

отбрасываем. Уравнения (20.10) переписываются: dS = fdN,

dN = Sdϕ.

В итоге получается одно дифференциальное уравнение с разделяющимися переменными

dSS = fdϕ.

Его интегрирование дает искомую связь:

S	dS	α
∫1		=∫ fdϕ, ln S SS12	=α f ,	(20.11)
S2	S	0

S1 = S2eα f .

Решение системы трех уравнений (20.8, 20.9 и 20.11):

137