Математический анализ_ЗФО_1 курс

y¢ = ((x + 8)ctg x)¢	æ		1		ö
	= (x +8)¢ ctg x + (x +8)(ctg x)¢ = ctg x + (x +8)ç	-				÷ .
			sin	2
	è				x ø

Производная функции в точке x0 = π/4:

æ

ö

æ p ö

p

æ p

öç

1 ÷

p +

32

1

p +

32

4

y¢ç

÷

= ctg

+ ç

+

8

֍

-

÷

=1-

×

=1-

×

=

2

è

4 ø

4 è 4

øç

sin2

p

÷

4

æ

2 ö

4

2

è

4 ø

ç

÷

è

2 ø

=1-

p + 32

=

2 -p - 32

=

-p -30

.

2

2

2

Пример 6. Найти производную функции

f (x )=

1- 4x

в точке x0 = 1.

2x +1

Решение. Воспользуемся правилом нахождения производной частного:

æ	f (x)	ö¢	=	f	¢	(x)g(x) - f			¢
ç		÷							(x)g (x) .
ç		÷				g	2	(x)
è g(x)		ø

Тогда

æ1- 4x

¢

1

- 4x ¢

2x +1

- 1-

4x

)(

2x +

1 ¢

-4

(

2x +1

- 2 1

- 4x

)

ö

(

) (

)

(

)

)

(

y¢ = ç

÷ =

=

=

+1

(2x +

1)

2

(2x +1)

2

è 2x

ø

=

-8x - 4 - 2 +8x

= -

6

.

(2x +1)2

(2x +1)2

Производная функции в точке x0 = 1:

y¢(1 )

= -

6

= -

2

.

(2 +1)2

3

Пример 7. Найти производную функции

f (x )=

cos x

в точке x0 = 0.

ex

+1

Решение. Воспользуемся правилом нахождения производной частного:

æ

(x)

ö

¢

=

¢

¢

ç f

÷

f

(x)g(x) - f (x)g

(x) .

ç

(x)

÷

g

2

(x)

è g

ø

Тогда

æ cos x ö¢

(cos x)¢ (ex

+1)- cos x (ex

+1)¢

-sin x

(ex +1)- cos x ×ex

y¢ = ç

÷ =

=

.

x

(

)

2

(

)

2

è e

+1 ø

e

x

e

x

+1

+1

Производная функции в точке x0 = 0:

-sin 0

(

e0 +1

- cos 0 ×e0

1

y¢(0 )=

)

= -

.

(

)

2

e

0

4

+1

Производная сложной функции

Сложная функция – это функция, аргументом которой является функция. Обозначают это так: g( f (x)) .

К примеру, пусть g – функция арктангенса, а f – натурального логарифма, тогда сложная функция g( f (x)) = arctg(ln x) .

Утверждение:

Пусть функция f : X ® Y Ì R дифференцируема в точке x Î X , а функция

g : Y ® R дифференцируема в точке y = f (x) ÎY , тогда композиция этих функций

g o f : X ® R дифференцируема в точке x Î X , причем

¢

¢

¢

(g o f ) (x) = g ( f (x))× f (x)

¢

или

¢

¢

[g(f (x))]

= g (f (x))× f (x) .

Пример 1. Вычислить производную сложной функции y = ln tg5x

y¢ = (ln tg5x)¢ =

1

(tg5x)¢ =

1

×

1

×(5x ¢) =

1

×

1

×5.

tg5x

cos2 5x

cos2

tg5x

tg5x

5x

Пример 2. Вычислить производную сложной функции y = cos6 x

Решение. Основная функция является степенной y = u 6 , а промежуточная u = cos x

– тригонометрической, поэтому сначала находим производную по формуле производной степенной (сложной) функции и умножаем на производную косинуса(элементарной функции).

(cos6 x)¢ = 6 cos5 x × (cos x)¢ = 6 cos5 x ×(- sin x) = -6 cos5 x ×sin x .

Пример 3. Вычислить производную сложной функции y = log

3

2x - 3

.

Решение.

2x + 4

Основная

функция

логарифмическая,

промежуточная

дробно-

рациональная.

Сначала

используется

формула

дифференцирования

сложно

логарифмической функции, а затем правила дифференцирования частного

2x - 3

.

3 ö¢

ö¢

2x + 4

æ

2x -

1

æ 2x - 3

çlog

÷

=

×ç

÷

=

3 2x +

2x

-

3

ö

2x + 4

è

4 ø

æ

è

ø

ç

×ln 3÷

2x

+ 4

è

ø

(2x - 3)¢

× (2x + 4)- (2x - 3)× (2x

+ 4)¢

æ

2x - 3

ö

=

(2x + 4)2

: ç

×ln 3

÷

=

2x + 4

è

ø

2(2x + 4)- (2x - 3)2

æ

2x - 3

ö

4x + 8 - 4x +

6

(2x

- 3)ln 3

=

: ç

× ln 3÷ =

:

=

(2x + 4)2

2x + 4

(2x + 4)2

(2x + 4)

è

ø

=

14

×

(2x + 4)

=

14

=

14

.

(2x + 4)2

(2x - 3)ln 3

(2x + 4)(2x - 3)ln 3

(4x 2

+ 2x -12) ln 3

Пример 4. Вычислить производную сложной функции y = 3

ln(1 + 32 x-1 )+

3

.

cos(2 - x)

Решение. Первое слагаемое представим в виде степенной функции и применим

формулу дифференцирования степенной функции (для сложной функции), со вторым

слагаемым поступим также, ведь

3

= 3(cos(2 - x))-1 , тогда:

cos(2 - x)

¢

æ

1

ö

¢

=

y¢ = ç(ln(1 + 32 x-1 ))3 ÷

+ 3((cos(2 - x))-1 )

ç

÷

è

ø

1

2x-1

-

2

2 x-1

¢

æ

1

ö

¢

=

(ln(1 + 3

)) 3

× (ln(1 + 3

))

+ 3ç

-

÷(cos(2 - x)) =

2

3

ç

cos

(2

÷

è

- x)ø

далее в первом слагаемом преобразуем степенную функцию и находим производную сложной логарифмической функции, во втором слагаемом используем формулу дифференцирования сложной функции косинуса, получим:

1

1

2 x-1

¢

3

¢

=

ln 2 (1 + 32 x-1 )×

1 + 32 x-1

× (1 + 3

)

-

×

(- sin (2

- x))× (2 - x) =

33

cos2 (2 - x)

¢

2 x-1

ln 3 × (2x -

¢

3sin (2 - x)(2

¢

¢

)

2

×32 x ×

1

×ln 3

3sin (2 - x)

=

1 + 3

1)

+

- x

==

3

-

=

3(1 +

2 x

-1

)

3

2

(1

2 x

-1

)

cos2 (2 - x)

æ

2 x

1

ö

2

2 x-1

cos2 (2 - x)

3

ln

+ 3

3ç1 + 3

×

÷

3 ln

(1 + 3

)

3

3sin (2 - x)

è

ø

2 ×32 x ln 3

=

3(3 + 32 x )3

ln 2 (1 + 32 x-1 ) -

.

cos2 (2 - x)

Производная высших порядков

Если функция

f : X ® R дифференцируема в любой точке x Î X ,

то на

множестве Х возникает новая функция

f ¢ : X ® R , значение которой в точке x Î X

¢

равно f (x) .

Эта функция f ¢ : X ® R сама может оказаться дифференцируемой, т.е. может

иметь производную (f ¢ ¢): X ® R , которая по отношению к исходной функции

f

называется второй производной от f

и обозначается

¢¢

или

d 2 f

. И так далее,

dx 2

f (x)

если мы найдем f (n-1) ) (x)

– n-1-ю производную определенную на Х, то по индукции,

производная n-го порядка определяется формулой f

(n)

(x) или

d n f

.

dx n

Пример 1. Вычислить вторую производную функции y = x2 ln(x2 +1) .

Решение. Найдем первую производную, используя формулу нахождения производной

произведения, а также правило дифференцирования сложной функции.

1

¢

2

2

¢

2 ¢

2

2

2

¢

2

2

2

¢

(

)

(

)

x2 +1

y =

x

ln(x

+1)

=

x

ln(x

+1) + x (ln(x

+1)) = 2x ln(x

+1) + x

(x

+1)

=

=

2x ln(x

2

+

1) + x

2

2x

=

2x ln( x

2

+1) +

2x3

x2

x2 +1 .

+1

Найдем вторую производную, используя формулы нахождения производной частного, производной произведения, а также правило дифференцирования сложной функции.

æ		2					2x			3		¢												2							2		¢			(					3 ¢				2		)		(		3		2		¢
												ö																											2x				) (					-				x	)( )
y¢¢ = ç 2x ln(x +1) +												÷ = (2x ¢)ln(x													+1) + 2x (ln(x							+1))			+									x		+1			2x					+1		=
						2																																								(			)	2
è							x	+1 ø																																							x2
																																																+1
					2x							6x2			(	x2	+1 -					(		2x3		)	2x
= 2ln(x2 +1) + 2x										+										)									=
				x	2 +1											(	x		2			)	2
																				+1
= 2ln(x	2	+1) +	4x2				+	6x4 + 6x2 - 4x4														=			2 ln(x			2	+1) +	4x2				+	2x4 +						6x2			.
			x2 +									(				)		2												x2		+			(						)	2
					1								x	2																			1			x		2		+
															+1																										1

Пример 2. Вычислить вторую производную функции y = x2 + e2x . Решение

Найдем первую производную, используя правило дифференцирования сложной функции.

¢

1

2x + e2 x (2x)¢

2x + 2e2 x

2

2 x

2

2 x

y¢ = ( x

+ e

) =

(x

+ e

)¢ =

=

=

2 x

2

+ e

2 x

2 x

2

+ e

2 x

2 x

2

+ e

2 x

=

x + e2x

.

x2 + e2 x

Найдем вторую производную, используя формулу нахождения производной

частного, а также правило дифференцирования сложной функции.

ö¢ (x + e2 x )¢ (

)-(x + e2 x )(

)¢

y¢¢ =

æ x + e2 x

x2 + e2 x

x2 + e2 x

ç

÷ =

=

2

è x2 + e2x

ø

(

x

2

+ e

2 x

)

(x2 + e2x )¢

(1+

2e2 x )(

x2 + e2 x )-(x + e2x )

2

x2 + e2 x

=

=

(

)2

x2 + e2x

(2x + 2e2 x )

(1+

2e2x )(

x2 + e2 x )-(x + e2 x )

2

x2 + e2 x

=

=

(x2 + e2 x )

=

(

2x

)(

2

2 x

) (

2 x

)

2

= x + e + 2x e + 2e - x - 2xe - e =

1+ 2e

x

+ e

-

x + e

2

2x

2 2x

4 x

2

2 x 4 x

(x2 + e2 x )

x2 + e2x

(x2 + e2 x )3

=

e2x + 2x2e2 x + e4 x - 2xe2 x

.

(x2 + e2 x )3

Пример 3. Найти производную n-ого порядка функции y = e1-3x . Решение. Преобразуем функцию

1-3 x

y = e1-3x = e 2 .

Найдем первую производную:

æ	1-3x	ö¢	1-3 x
y¢ = çe	2 ÷		= e 2
è	ø

Тогда вторая производная равна

	æ		3		1-3 x	ö¢		3
	y¢¢ = ç	-		e 2 ÷			= -		e
			2					2
	è			ø

æ1-3x ö¢

= e

1-3x

æ

3

ö

ç

÷

2

ç -

÷.

2

2

è

ø

è

ø

1-3 x

æ1-3x ö¢

= e

1-3 x

æ

3

ö2

2

ç

÷

2

ç

-

÷ .

2

2

è

ø

è

ø

Легко увидеть, что каждая последующая производная будет получаться

	æ	-	3	ö	. Следовательно,
	умножением предыдущей функции на коэффициент ç			÷
			2
	è			ø

	(n)		1-3 x	æ		3 ön
y		= e 2 ç			-		÷ .
						2
		è					ø

Исследование функций методами дифференциального исчисления

	1.	Условия монотонности функции
Утверждение: между характером монотонности дифференцируемой на интервале
а;b функции									¢		на этом интервале имеется
	f : a;b ® R и знаком ее производной f (x)
следующая взаимосвязь:		f	¢	> 0 Þ		f	возрастает Þ f				¢
			(x)								(x) > 0
		f	¢	³ 0 Þ		f	не убывает Þ f				¢
			(x)								(x) ³ 0
			¢						¢
			f (x) º 0 Þ				f – const Þ f			(x) º 0
			¢			f	убывает Þ f			¢
			f (x) < 0 Þ							(x) < 0
	f	¢									¢
		(x) £ 0 Þ f				не возрастает Þ f (x) £ 0 .
Пример. Найти промежутки возрастания и убывания функции f (x) = x3 -12x +11 .
				¢				2	-12 и приравняем её к нулю. Итак,
Для этого найдем производную f (x) = 3x
3x 2 -12 = 3(x 2	- 4) = 0 , отсюда x			= -2, x	2	= 2 .
			1

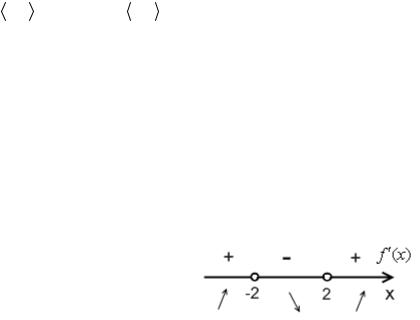
Отметим найденные точки на числовой прямой и расставим знаки:

Таким образом, функция возрастает ( f ­ ) на промежутке (- ¥; - 2)È (2; + ¥) и

убывает ( f ¯ ) на промежутке (- 2; 2).

Ответ: f ­ : (- ¥; - 2)È (2; + ¥) f ¯ : (- 2; 2).

2. Экстремумы функции

Точками экстремума называют точки, в которых функция принимает максимальное или минимальное значения.

Определение:

Точка х0 называется точкой строгого локального максимума (минимума)

функции f (x) , если для всех x из некоторой окрестности точки х0 (U (x0 )) выполняется неравенство f (x) < f (x0 ) ( f (x) > f (x0 ) ).

Теорема Ферма:

(необходимое условие локального экстремума)

Пусть f (x) непрерывна на замкнутом отрезке [a; b] и дифференцируема на (a; b). Если х0 – внутренняя тока экстремума, то f ¢(x0 ) = 0 .

Теорема:

(достаточное условие локального экстремума)

Пусть f (x) непрерывна на замкнутом отрезке [a; b], дифференцируема на (a; b) и

х0 Î (a; b).

Если f ¢(x) при переходе через точку х0 меняет знак с «+» на «-», то х0 – точка локального максимума.

Если f ¢(x) при переходе через точку х0 меняет знак с «-» на «+», то х0 – точка локального минимума.

Если знак f ¢(x) при переходе через точку х0 не меняется, то экстремума в точке

х0 не существует.

Пример. Найти экстремумы функции f (x) = 3x 4 - 4x3 -12x 2 + 2 .

Для начала найдем точки возможного экстремума (критические точки), найдя производную и приравняв ее к нулю:

f¢(x) = 12x3 -12x 2 - 24x = 0

x3 - x 2 - 2x = 0 , далее х(x 2 - x - 2)= 0 .

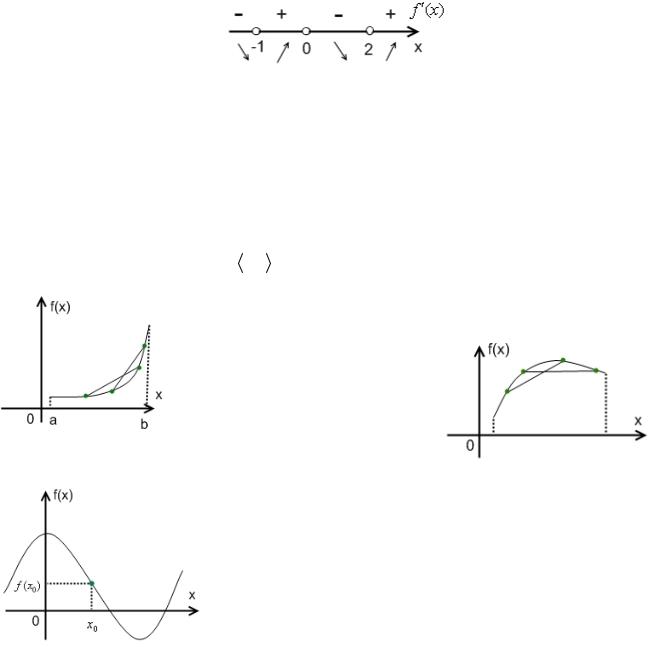
Отсюда х = 0, х = -1, х = 2 . Отметим найденные точки на числовой прямой и

расставим знаки.

f ¢(x) = 12х(x - 2)(x +1)

Таким образом, по теореме о достаточном условии локального экстремума, точки x = -1 и x = 2 являются точками локального минимума, так как производная f ¢(x) , проходя через эти точки, меняет знак с «-» на «+». Точка x = 0 – точка локального максимума, так как производная f ¢(x) , проходя через эту точку, меняет знак с «+» на «-».

Ответ: xmin = -1, xmin = 2 и xmax = 0 .

3. Выпуклость и точки перегиба графика функции

Определение:

Пусть f задана на отрезке а;b .

Функция f называется выпуклой вниз на этом отрезке, если ее график обладает следующим свойством: хорда, соединяющая две любые точки графика, лежит выше графика.

Функция f называется

выпуклой вверх на этом отрезке,

если хорда, соединяющая любые две точки графика, лежит ниже графика.

Определение:

Точка M (x0 ; f (x0 )) называется точкой перегиба графика функции f (x) , если существует такая окрестность точки х0 (U (x0 )), в пределах которой график функции слева и справа от точки х0 имеет разные направления выпуклости.

Теорема:

Для того, чтобы функция f : a; b ® R , дважды дифференцируемая на интервале

а;b , была выпуклой вниз (вверх) на этом интервале необходимо и достаточно, чтобы

f	¢¢	¢¢
	(x) ³ 0 ( f	(x) £ 0 ) на интервале а;b .

Пример. Найдем промежутки выпуклости и точки перегиба функции y = x3 . Для этого вторую производную функции и

приравняем ее к нулю:

y¢ = 3x 2 y¢¢ = 6x

6x = 0

x = 0

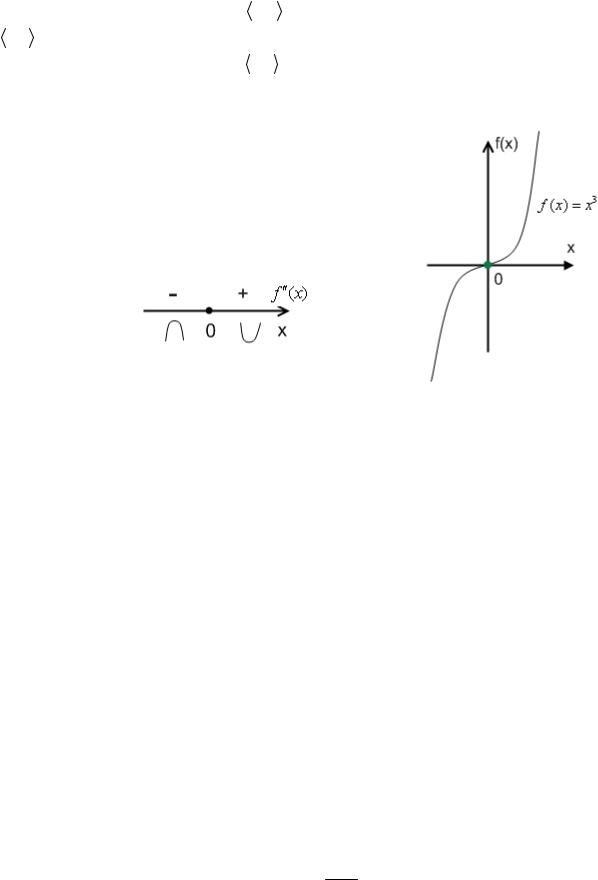
Отметим найденную точку на числовой прямой и расставим знаки:

Таким образом, на промежутке (- ¥; 0) функция выпукла вверх, а на промежутке (0; + ¥) – выпукла вниз.

Т.к. в точке х = 0 меняется направление выпуклости функции, то х = 0 – точка перегиба функции y = x3 .

)

Ответ: (- ¥; 0) – f (x)

(

(0; + ¥) – f (x)

х = 0 – точка перегиба.

4. Асимптоты графика функции

Определение:

Прямая y = kx + b называется асимптотой графика функции y = f (x) при x ® ¥ , если расстояние между этим графиком и прямой стремится к нулю при x ® ¥ , т.е.

f (x) - (kx + b) ® 0, x ® ¥

Существует три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальная асимптота: прямая вида x = A

lim f (x) = ¥ ,

x®A

(т.е. вертикальные асимптоты – это ограничения на х, например точки, в которых функция не определена).

Горизонтальная асимптота: прямая вида y = A

lim f (x) = A

x®¥

(т.е. горизонтальные асимптоты – это ограничения на у)

Наклонная асимптота: прямая вида y = kx + b, k ¹ 0, k ¹ ¥ .

Коэффициент k вычисляется по формуле:

f (x)

k = lim

x®+¥	x
( x®-¥)

Коэффициент b вычисляется по формуле:

b = lim [f (x) - kx]

x®+¥ x®-¥

Теорема:

Для того, чтобы график функции y = f (x) имел наклонную асимптоту при х ® +¥ ( х ® -¥ ) необходимо и достаточно, чтобы существовали пределы:

lim	f (x)	= k	и lim [f (x) - kx]= b .
x®+¥	x		x®+¥
( x®-¥)			x®-¥

Пример 1. Найти асимптоты графика функции f (x) = x + 5 . x - 3

Точка x = 3 – вертикальная асимптота, т.к. функция в этой точке неопределенна и

lim x + 5 = ¥ .

x®3 x - 3

Найдем горизонтальную асимптоту:

lim x + 5 = 1, следовательно y = 1 – горизонтальная асимптота.

x®¥ x - 3

Далее, ищем наклонную асимптоту. Для этого сначала найдем коэффициент k.

k = lim

f (x)

= lim

х + 5

= 0 .

x®+¥

x

x®+¥

х(х - 3)

( x®-¥)

( x®-¥)

Следовательно, наклонных асимптот нет и коэффициент b искать не нужно.

Ответ: x = 3 , y = 1.

Пример 2. Найти наклонные асимптоты графика функции

f (x) =

x 2

-1

.

x

Наклонная асимптота – это прямая вида y = kx + b, k ¹ 0,

k ¹ ¥ .

Найдем коэффициент k:

х2 -1

f

(x)

х 2

-1

k = lim

=

lim

х

=

lim

= 1

x

х

х

2

x®+¥

x®+¥

x®+¥

( x®-¥)

( x®-¥)

( x®-¥)

Далее, коэффициент b:

b = lim [f (x) - kx]= lim

é

х

2

-1

ù

é

х

2

-1 - х

2 ù

ê

-1× хú

= lim

ê

ú

= 0

х

х

x®-¥

x®-¥ë

û x®-¥ë

û

x®+¥

x®+¥

x®+¥

Т.к. k = 1 , а b = 0 , то наклонная асимптота – это прямая у = kх + b = 1× x + 0 = x . Ответ: у = х .

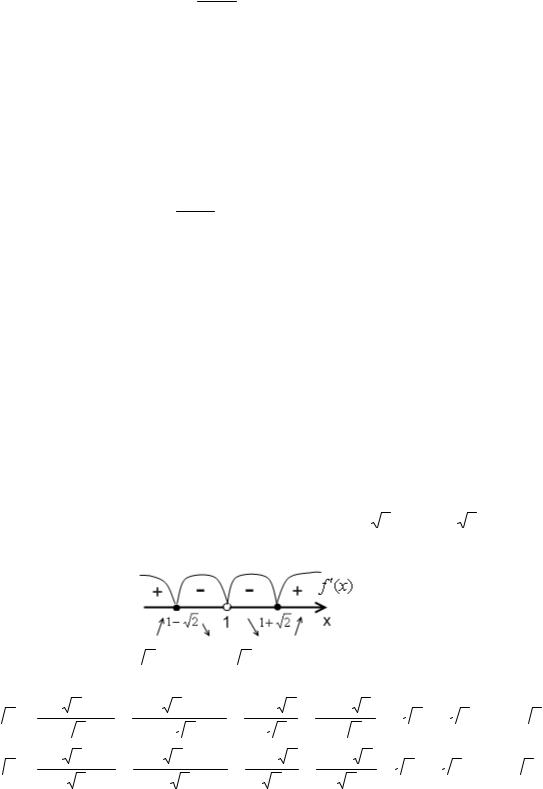
Алгоритм исследования графика функции

Построим график функции f (x) = x 2 +1 . x -1

1. ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ:

x Î (- ¥; 1)È (1; + ¥)

2. ТОЧКИ ПЕРЕСЕЧЕНИЯ ГРАФИКА С ОСЯМИ КООРДИНАТ:

С осью ОУ: x = 0 f (x) = -1, значит (0; -1) – точка пересечения.

	С осью ОХ: y = 0	x 2	+1	= 0	x ÎÆ
		x	-1

3. АСИМПТОТЫ:

Вертикальная асимптота x = 1;

Горизонтальная асимптота: lim x 2 +1 = ¥ . Следовательно, горизонтальных

x®¥ x -1

асимптот нет.

Наклонные асимптоты:

	f (x)			х 2 +1			х 2 -1
k = lim		= lim		х -1	=	lim		= 1,
	x
x®+¥		x®+¥		х		x®+¥	х(x -1)
( x®-¥)		( x®-¥)				( x®-¥)

b = lim [f (x) - kx]= lim

é х 2

+1

-1× хù = lim

é х 2

+1 - х 2

+ x

ù = lim

é

x +1

ù = 1 ,

ë х

-1

ë

х -1

x®-¥

x®-¥

û

x®-¥

û

x®-¥

ë

х -1û

x®+¥

x®+¥

ê

ú

x®+¥

ê

ú

x®+¥

ê

ú

Т.к. k = 1 и b = 1, то наклонная асимптота – это прямая у = x +1 .

4.ПРОМЕЖУТКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ, ТОЧКИ ЭКСТРЕМУМА:

Производная функции

¢

2x(x -1) - (x 2 +1) ×1

x 2

- 2x

-1

f

(x) =

=

(x -1)2

(x -1)

2

x 2 - 2x -1

= 0

, тогда x

2

- 2x -1 = 0, x ¹ 1 , отсюда x

= 1 -

2 , x

2

= 1 + 2 .

(x -1)2

1

Отметим найденные точки на числовой прямой и расставим знаки:

Таким образом, xmax = 1 - 2 , xmin = 1 + 2 . Вычислим значение функции в этих точках:

( ) (1 - 2 )2 +1 1 - 2 2 + 2 +1 4 - 2 2 2(2 - 2 ) ( )

f 1 - 2 = = = = = - 2 2 - 2 = 2 - 2 2 1 - 2 -1 - 2 - 2 - 2

( ) (1 + 2 )2 +1 1 + 2 2 + 2 +1 4 + 2 2 2(2 - 2 ) ( )

f 1 + 2 = = = = = 2 2 + 2 = 2 + 2 2

1 + 2 -1

2

2

2

5.

ТОЧКИ ПЕРЕГИБА:

Найдем вторую производную:

æ

x

2

- 2x -1

ö¢

(2x - 2)(x -1)

2

- (x

2

- 2x -1)× 2(x -1)

¢¢

ç

÷

(x -1)4

f (x) = èç (x -1)2

ø÷

=

=