Математический анализ_ЗФО_1 курс

			sin a ×cos b =
	òsin аx cos bxdx		=		1		(sin (a + b )+ sin (a - b ))
			2
	òcos аx cos bxdx	–	cosa ×cos b =
8
	òsin аx sin bxdx		=		1		(cos(a + b )+ cos(a - b ));
			2
			sin a ×sin b =
			=	1		(cos(a - b )- cos(a + b ))
			2

переход к интегралу от суммы функций

Пример 1. Найти интеграл ò

dx

.

5 + sin x + 3cos x

Решение. Данный интеграл от тригонометрических функций вида òR(sin x,cos x) ×dx

«берется»

с помощью

универсальной

тригонометрической

подстановки: tg

x

= t , тогда

2

sin x =

2t

;dx

=

2dt

;

cos x =

1

- t 2

. Получим:

1+ t

1

+ t 2

2

1+ t 2

ò

dx

= ò

1

3(1-t 2 )

×

2dt

=

5 + sin x +

3cos x

2t

1+ t 2

5 +

+

1+ t 2

1+ t 2

= 2ò

1 + t 2

×

dt

= 2ò

dt

= ò

dt

=

5

+

5t

2

+ 2t +

3 -

3t

2

1

+ t

2

2t

2

t

2

+ 2t +8

+ t + 4

dt

dt

1

=

=

=

t +

2

= u

=

òæ

1

æ

1 ö

2 ö

1

ò

æ

1 ö2

æ

15

ö

2

2

dt = du

çt

+ 2 ×

×t + ç

÷

÷ -

+ 4

çt

+

÷

+ ç

÷

ç

2

è 2 ø

÷

4

è

2 ø

ç

2

÷

è

ø

è

ø

du

2

2u

2

2t +1

2

2tg

x

+1

= ò

2 =

arctg

+ C =

arctg

+ C

=

arctg

2

+ C .

2

æ

15

ö

15

15

15

15

15

15

u

+ ç

÷

ç

2

÷

è

ø

Пример 2. Найти интеграл òsin 3 x × cos4

x × dx .

Решение.

Так

как

степеньsin x нечетная,

а у cos x

–

четная,

то

рекомендуемая

подстановка cos x = t .

òsin 3 x ×cos4 xdx = òsin 2 x ×cos4 x ×sin xdx = òsin 2 x ×cos4 xd (cos x) =

ò(1 - cos2 x)×cos4 xd (cos x) =ò(1 - t 2 )t 4 dt = -

t 5

+

t 7

+ с = -

cos5 x

+

cos7 x

+ c .

5

7

5

7

Пример 3. Найти интеграл ò

dx

.

3cos

2

x

+ 4sin

2

x

Решение. Так как подынтегральная функция – четная относительно sin x и cos x , то

рекомендуемая подстановка tgx = t

(№2 Таблица 1),

тогда sin 2 x =

t 2

,

cos2 t =

1

,

dx =

dt

.

1

+ t 2

1 + t 2

1+ t 2

ò

dx

=

ò

1

×

dt

= ò

dt

= 1

ò

dt

=

3cos

2

x +

4sin

2

x

3

4t

2

1

+ t

2

3

+ 4t

2

æ

ö

2

+

4

3

t 2

+ ç

÷

1 + t

2

+ t

2

1

ç

2

÷

è

ø

=

1× 2

arctg 2 × t + с =

1

3

arctg 2 × tg x + с.

4 ×

3

3

2

3

Пример 4.

Найти

òsin

x

×cos

x

×dx .

3

4

Решение. Применяя формулу преобразования произведения тригонометрических

функций в сумму (№8 Таблица 1), получим

1

b

1

æ x

x

ö

1

æ x

x

ö

f (x )=

×

ò f (x )dx

=

òsin

ç

+

÷

×dx +

òsinç

-

÷

×dx =

b - a

2

2

a

è

3 4

ø

è

3 4

ø

1

12

òsin

7x

æ

7x ö

1

×12òsin

x

æ

x ö

6

7x

x

=

×

× d ç

÷ +

× d

ç

÷ = -

cos

- 6 cos

+ с.

2

7

12

12

2

12

7

12

12

è

ø

è

12 ø

Пример 5. Найти

òsin 2 x × cos4 x × dx .

Решение. Т.к. это интеграл вида òsin m x cosn xdx и степени у sin x

и cos x четные, то

применяется понижение степени тригонометрических функций (№7 Таблица 1).

2

x =

1 - cos 2x

2

x =

1 + cos 2x

4

x =

æ1

+ cos 2x ö

2

1

(1

+ cos 2x)

2

sin

, cos

Þ cos

ç

÷

=

, тогда

2

2

2

4

è

ø

òsin 2 x × cos4 x × dx =			1	ò(1- cos 2x)× (1+ cos 2x)2 dx =
		8
=	1	ò(1+ cos 2x - cos2 2x - cos3 2x)×dx =
8

Далее, преобразуем

cos2 x = 1 + cos 2x Þ cos2 2x = 1 + cos 4x Þ cos3 2x = cos2 2x × cos 2x = 1 + cos 4x ×cos 2x ,

					2																2																	2
и продолжим равенство
											1		æ												1+ cos 4x						1		+ cos 4x			ö
									=					òç1+ cos 2x -																-				×cos 2x ÷×dx			=
											8															2							2
													è																							ø
													=				1			ò(1+ cos 2x - cos 4x - cos 4x ×cos 2x)×dx.
														1		16						1
Так как				cos 4x ×cos 2x =											cos 2x +								cos 6x,				получим
													2								2
						òsin		2								4								1		æ		1							1		ö
									x × cos									x		× dx	= =					òç1	+			cos 2x - cos 4x -						cos 6x ÷		×dx =
																								16				2							2
																										è											ø
=	x	+	sin 2x			-	sin 4x			-		sin 6x								+ с.
16				64	64								192

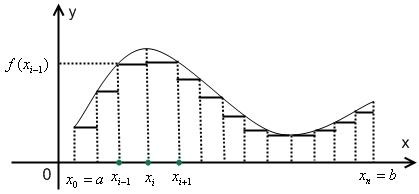
Определенный интеграл

1. Задача, приводящая к понятию определенного интеграла

Будем решать задачу, которую решал еще Архимед:

Нужно найти площадь под некоторой непрерывной функцией f (x) на отрезке

[a; b].

Также как и Архимед, будем действовать методом исчерпания фигуры посредством простейших фигур – прямоугольников, площади которых мы вычислять умеем.

Разобьем отрезок [a; b] точками x0 , x1 , x2 ,..., xn			такими, что
получим отрезки [xi-1 ; xi ],	a = x0 , < x1 < x2 < ... < xn-1		< xn = b ,
	i = 1,2,3,...,n .
Таким образом, мы можем приближенно вычислить искомую площадь S как сумму
площадей получившихся прямоугольников.
Вычислим площадь i -го прямоугольника:
	Si = (xi - xi -1 ) × f (xi-1 )
Обозначим xi - xi-1	= Dxi , тогда
	S i = D x i × f ( x i - ) , i = 1,2,3,...,n .
Таким образом, сумма площадей всех прямоугольников приближенно равна
площади искомой фигуры:
	n
	åDxi × f (xi -1 ) » S		(*)
	i=1
Очевидно, что чем мельче разбиение, тем точнее это приближение. Т.е.
		n
	lim	åDxi × f (xi-1 ) = S	(**)
	l®0	i=1

Здесь l – длина наибольшего из отрезков разбиения.

Полученная сумма (*) называется интегральной суммой функции f , соответствующей разбиению [xi-1 ; xi ], i = 1,2,3,...,n отрезка [a; b].

Предел интегральных сумм (**) называется интегралом (определенным

интегралом) функции f по отрезку [a;	b] и обозначается
b		n
ò f (x)dx = lim		å f (xi-1 )Dxi .
a	l®0	i=1

Свойства определенного интеграла:

1. Теорема:			b] функции, то их линейная комбинация
Если	f и g – интегрируемые на [a;
af + bg также является интегрируемой на [a; b] функцией, причем:
	b				b	b
	ò[af (x) + bg(x)]dx = a ò f (x)dx + b ò g(x)dx
	a				a	a
2. Теорема (аддитивность):
Если a < b < c и функция		f интегрируема на отрезке [a; c], то справедливо
равенство:
		c	b			c
		ò f (x)dx = ò f (x)dx + ò f (x)dx .
		a	a			b
3. Теорема (монотонность):
Если a £ b и функции f1		и f2 интегрируемы на отрезке [a; b], причем
f1 (x) £ f 2 (x)	для любых x Î[a;	b], то
		b	b
		ò f1 (x)dx £ ò f 2 (x)dx .
		a	a
4. Утверждение (формула интегрирования по частям):
Если	f и g – непрерывны и дифференцируемы на отрезке [a; b] и имеют
непрерывные производные на [a; b], то справедливо равенство:
	b					b
	ò f (x)g ¢(x)dx = f (x)g(x)				ba - ò f ¢(x )g(x)dx
	a					a
	Формула Ньютона-Лейбница
Пусть	f : [a; b]® R непрерывная на [a; b] функция, тогда:

1.Функция f имеет первообразную F (x)

2.Справедлива формула ньютона-Лейбница:

b

ò f (x)dx = F (x) ba

a

= F (b) - F (a) ,

где F (x) – любая из первообразных функции f на отрезке [a; b].

2. Некоторые приложения определенного интеграла

Вычисление площадей плоских фигур

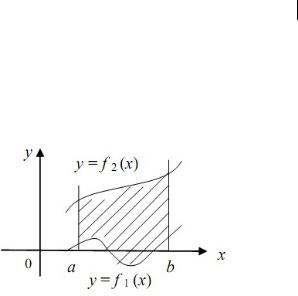
Площадь криволинейной трапеции, ограниченной графиками функций у = f1 (x) ,

у = f2 (x) , прямыми x = a и x = b и f1 (x) £ f 2 (x) для любых x Î[a; b] (Рисунок 2) равна:

b

S = ò[f2 (x) - f1 (x)]dx

a

Рисунок 2

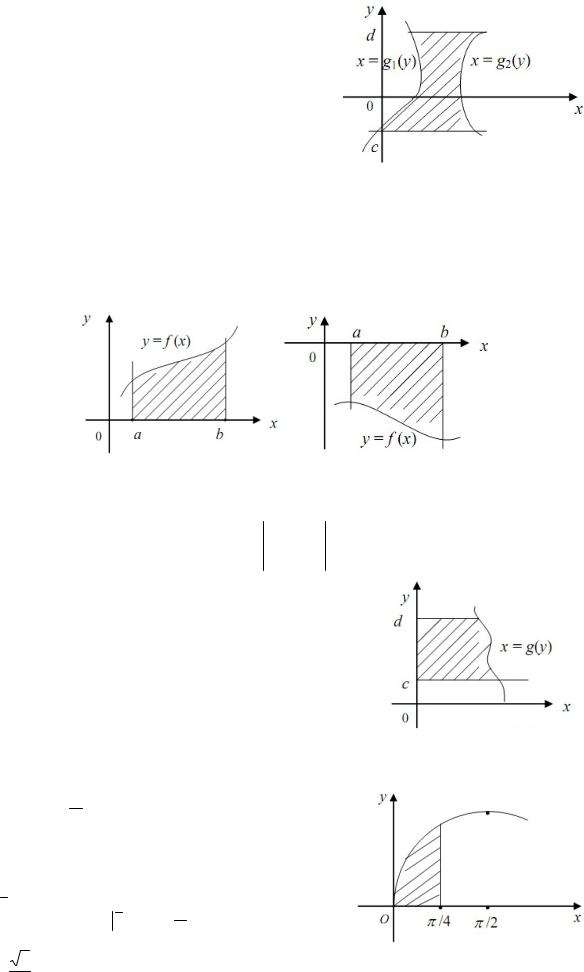
Если криволинейная трапеция ограничена прямыми y = c, y = d , и кривыми x = g1 ( y) и

x = g 2 ( y) и g1 ( y) £ g2 ( y) для любых y Î[c; d ]

(Рисунок 3), то ее площадь вычисляется по формуле:

d

S = ò[g2 ( y) - g1 ( y)]dy .

с

Рисунок 3

Если непрерывная кривая задана в прямоугольных координатах уравнением у = f (x) ( f (x) > 0, для любых x Î[a; b]), то площадь плоской фигуры, ограниченной

этой кривой, прямыми x = a и x = b и осью Ох (Рисунок 4), вычисляется по формуле:

b

S = ò f (x)dx .

a

Рисунок 4 Рисунок 5

Если f (x) £ 0, для любых x Î[a; b] (Рисунок 5), то в этом случае

b

S = ò f (x)dx .

a

Площадь криволинейной трапеции, ограниченной прямыми y = c, y = d , непрерывной кривой

x = g( y) ( g( y) > 0, для любых y Î[c; d ]), и осью Оу (Рисунок 6) вычисляется по формуле:

d

S = òg( y)dy .

c

Рисунок 6

Пример 1. Найти площадь фигуры, ограниченной линиями y = sin x ,

y = 0 , 0 £ x £ p (Рисунок 7). 4

Решение. Данная фигура является криволинейной трапецией, прилегающей к оси Ох, поэтому ее площадь

p

4

p

S = òsin xdx = -cos x 04

0

= 1 - 2 (кв.ед.).

= -sin p +1 =

4

Рисунок 7

2

Пример 2. Найти площадь фигуры, ограниченной кривыми y = 2x - x2 , y = x - 2 (Рисунок 8).

Решение.

Рисунок 8

Найдем точки пересечения данных кривых. Для этого решим систему

уравнений: íìy = 2x - x 2

Þ 2x - x 2

= x - 2, х 2

- х - 2 = 0, откуда

îy = x - 2

х1 = -1, у1 = -3 и х3 = 2,

у2

= 0 . Следовательно, кривые пересекаются в точках A(-1;-3) и

C(2; 0) . Таким образом, искомая площадь фигуры АВС

2

2

2

2

æ

1

3

1

2

ö

2

S = ò

(2x - x

- (x - 2))dx

=ò

(- x

- x + 2)dx =ç

-

x

+

x

+ 2x ÷

=

3

2

-1

-1

è

8

ø

-1

æ 1

1

9

æ

ö

ö

=

ç-

+ 2 +

4÷

-

ç

+

+ 2÷ =

(кв.ед.).

3

2

2

è

ø

è 3

ø

Пример 3. Найти площадь фигуры, ограниченной линиями y2 = 3x + 4, x - y - 2 = 0 (Рисунок 9).

Решение.

Рисунок 9

Найдем точки пересечения данных кривых:

ì

2

= 3x + 4

ì

2

= 3x + 4

íy

Þ íy

îx - y - 2 = 0

îx = y + 2

y 2 = 3( y + 2) + 4, y

2 - 3y -10 = 0 , y = -2 , y

2

= 5 .

1

Выразим y

2

= 3x + 4

Þ 3x = y

2

- 4

Þ x =

y 2

4

-

и найдем площадь фигуры:

3

3

5

5

æ

æ 1

2

4 öö

5

æ

1

2

10 ö

æ

1

3 1 2

10

ö

343

ò

ç

÷

ò

S =

ç y + 2

- ç

y

-

÷÷dy

=

ç

-

y

+ y +

÷dy = ç

-

y +

y +

y

÷

=

.

-2è

è 3

3

øø

-2è

3

3

ø

è

9

2

3

ø

-2

18

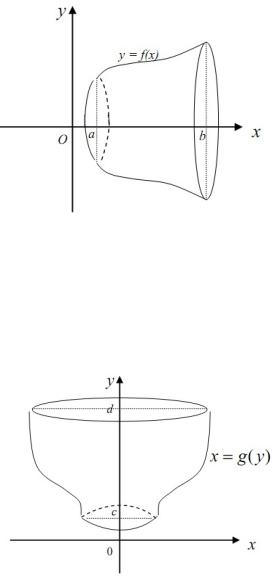
Вычисление объема тела вращения

Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой у = f (x) , осью Ох и прямыми x = a и

x = b вокруг оси Ох	(Рисунок 10), находится
по формуле
b	b
V = p ò y 2 dx = p ò f 2 (x)dx .
a	a
	Рисунок 10
Если вокруг	оси Ох вращается фигура, ограниченная кривыми у = f1 (x) ,

у = f2 (x) ( 0 £ f1 (x) £ f2 (x)		для любых x Î[a;
тела вращения вычисляется по формуле
		V = p òb (f 22 (x) -
		a
Объем	тела,	образованного

вращением вокруг оси Оу криволинейной трапеции, ограниченной кривой x = g( y) осью Оу и прямыми y = c, y = d (Рисунок 11), определяется по формуле

d d

V= p ò x 2 dx = p òg 2 ( y)dy .

сc

b]) и прямыми x = a и x = b , то объем

f12 (x))dx .

Рисунок 11

Если фигура ограничена кривыми x = g1 ( y) и x = g 2 ( y) ( 0 £ g1 ( y) £ g2 ( y) для любых y Î[c; d ]) и прямыми y = c, y = d , то объем тела, полученный при вращении этой фигуры вокруг оси Оу, можно найти по формуле

d

V = p ò(g 22 ( y) - g12 ( y))dy .

с

Пример. Найти объем тела, образованного при вращении вокруг оси Ох фигуры, ограниченной линиями 4 y = x2 , x + 4 y -12 = 0 (Рисунок 12).

Решение. Найдем точки пересечения кривых. Для этого решим систему уравнений

ì

x

2

ì

x 2

ì

x 2

ì4 y = x

2

ïy =

ï

4

ïy =

ïy

=

4

4

í

+ 4 y

-12

= 0

Þ í

x 2

Þ í

í

îx

ï

ï

2

ï

ïx + 4 ×

-12 = 0

îx

+ x

-12

= 0îx1

= -4, x2 = 3

4

î

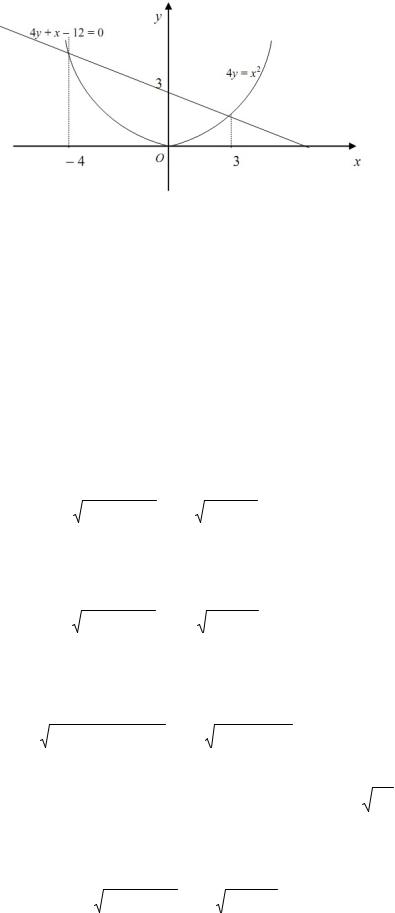
Рисунок 12

Следовательно,

V = p

æ

p ç9x

è

3 æ			æ					x		ö	2		æ		x	2 ö			2 ö					3 æ		3					x	2					x	4	ö
ò	ç				3 -								ç					÷	÷					ç				x +											÷
			ç							÷															-							-
	ç							4				- ç			4		÷		÷dx =p òç9							2													÷dx =
-4è			è							ø			è				ø		ø					-4è						16 16									ø
-	3				x	2	+			1		x	3	-			1		x	5	ö		3	æ				27				9						243		æ			4		64	öö	34
																					÷			= p ç27		-				+						-				- ç	- 36	-12 -		+		÷÷ = 54			p /
	4							48								80					ø			ç				4				16						80		è			3		5	÷	120
																							-4	è																						øø

Вычисление длины дуги кривой

Если дуга кривой задана уравнением у = f (x) (a £ x £ b) и функция f (x) имеет непрерывную производную в промежутке [a; b], то длина дуги кривой, содержащейся между двумя точками с абсциссами x = a и x = b , вычисляется по формуле:

b

b

¢

2

dx

=ò 1 + (y

¢ 2

l = ò 1 + (f (x))

)dx .

a

a

Если кривая задана уравнением x = g( y) в промежутке [c; d ] и функция x = g( y)

имеет непрерывную производную в этом промежутке, то длина дуги кривой

определяется по формуле:

d

d

l = ò

¢

2

dy

= ò 1 + (x

¢ 2

1 + (g ( y))

) dy .

c

c

Длина

дуги кривой,

заданной

параметрически x = j1 (t) ,

y = j2 (t)

(t1 £ t £ t2 ), где j1 (t), j2 (t) – непрерывно дифференцируемые функции, выражается

формулой

t2

t2

(t))

(t))

¢ 2

¢

2

¢

2

dt = ò (x

+

¢

2

dt) .

l = ò (j1

+ j(2

)

y(

t1

t1

Пример.

Вычислить длину

дуги

полукубической

параболыy = x3 от точки

A(1; 1) до точки B(4; 8) .

Решение. Так как кривая задана уравнением

видау = f (x) ,

то длина ее дуги

вычисляется по формуле

b

b

¢

2

dx =ò 1 + (y

¢ 2

l = ò 1 + (f (x))

)dx

a

a

								æ		3	ö¢		3			1
Найдем производную y¢ = ç x										2 ÷		=		x 2			, тогда
								ç		÷		2
								è		ø
4		æ	3		1	ö2	4		9			4 4					9			æ			9 ö
l = ò	1 +	ç		x	2	÷	dx = ò	1 +		xdx =					ò		1 + x × dç1 +							x ÷ =
		ç	2			÷			4
1		è				ø	1					9			1		4			è			4 ø
																		4		2	æ			9	3	4	8	æ		13		ö
																									ö 2
																	=		×		ç1	+			x ÷	=		ç10 10	-		13	÷ .
																		9		3				4			27			8
																					è				ø	1		è				ø

Приложения определенного интеграла в решении физических и экономических задач

Если непрерывная функция f (t) характеризует производительность труда рабочего в зависимости от времени t, то объем продукции, произведенной рабочим за промежуток времени от t1 до t2 , выражается формулой

t2

V = ò f (t)dt

t1

Если в функции Кобба-Дугласа затраты труда считать линейно зависимыми от времени, а затраты капитала неизменными, то объем продукции V за T лет равен

T

V = ò(at + b)egt dt .

0

Если проценты по вкладу начисляются непрерывно и их характеризует функция y = f (t) а удельная норма процента равна i, то дисконтированный доход К за время Т составляет

T

K = ò f (t)e-it dt .

0

Скорость оттока рабочей силы в момент времени Т можно определить при помощи уравнения восстановления

T

L(t) = f (t) + ò f (t)L(T - t)dt ,

t0

Где f (t) – доля тех, кто был вначале (при t = t0 ) и покинул предприятие в настоящее время, при t = T ; L(T - t) – скорость оттока людей, пришедших кому-то на смену; f (t)L(T -t) – полная скорость оттока заместителей, покидающих предприятие в настоящий момент.

Общую сумму S текущих издержек обращения и капиталовложений, сводимых к текущим затратам, можно определить по формуле

+¥

S = ò f (t)dt .

0

Если материальная точка движется прямолинейно со скоростью n =n (t) , то пройденный ею за промежуток времени от t1 до t2 путь

t2

S = òn (t)dt .

t1

Пример 1. Найти объем продукции, произведенной рабочим за третий час рабочего времени, если производительность труда описывается функцией

f (t) = 3t 2 - 2t +1 .

3

Решение. V

= ò(3t 2

- 2t +1)dt = (t 3 - t 2

+ t)

3

= 15 .

2

2

Пример 2. Найти объем произведенной продукции за 5 лет, если функция

Кобба–Дугласа g(t) = (1 + t)e3t .

é

¢

3t

ù

1

1

5

3t

ê f (t) = 1 + t, g (t) = e

ú

3t

5

5

3t

V = ò(1 + t)e

dt =

ê

1

3t

ú

=

(1

+ t e)

-

òe

dt =

0

ê f ¢(t) = 1,

g(t) =

e

ú

3

0

3

0

3

ë

û

=

1

(6e15 -1)-

1

e3t

5 =

1

(6e15 -1)-

1

(e15 -1)=

1

(17e15 - 2).

Пример 2.

3

9

0

3

9

9

Определить дисконтированный доход, если процентная ставка – 5 %,

первоначальные вложения – 5 млн р., прирост – 1 млн р. в год. Срок – 5 лет.

Решение. В нашем случае функция капиталовложений, согласно условию задачи,

является линейной и равна f (t) = k + lt , где k = 5 ,

l = 1, т.е.

f (t) = 5 + t . Удельная норма

процента i = 0,05 . Тогда дисконтированный доход равен:

5

é

¢

-0,05t

ù

= - 20(5

+ t )e-0,05t

5

5

K = ò(5 + t)e-0,05t dt = ê f (t)

= 5 + t,

g (t)

= e

-0,05t

ú

0 + 20òe-0,05t dt =

0

ê f ¢(t) = 1, g(t) = -20e

ú

0

ë

û

= 20(5 -10e-0,25 )- 400e-0,05t

5

= 20(5 -10e -0,25 )- 400(e-0, 25 -1)=

0

= 500 - 600e-0,25

» 32,72 (млн.р.).

Пример 3. Определить общую сумму текущих затрат, если функция,

характеризующая текущие издержки обращения и капиталовложения,

имеет вид

f (t) =

10

.

t 2 + 2t + 5

Решение.

d (t

+1)

+¥

10

R

10

R

dt

R

S = ò

dt

= lim

ò

dt = 10 lim

ò

= 10 lim

ò

=

t

2

t

2

2

+ 2t

+1 + 4

+1

2

+ 2

2

0

+ 2t + 5

R®+¥

0

+ 2t + 5

R®+¥

0 t

R®+¥

0 (t

)

1

x +

1

R

æ

R +1

1

ö

æ p

1 ö

10 lim

arctg

= 5 lim

çarctg

- arctg

÷

=

5ç

- arctg

÷ » 5(1,57 -) 0,46) » 5,55 .

R®+¥ 2

2

0

R®+¥è

2

2

ø

è

2

2

ø

Пример 4. Скорость движения точки n = 1 t3 м/с. Найти путь S, пройденный

2

точкой за время Т = 5с. после начала движения. Чему равна средняя скорость движения за этот промежуток?

			5			1		1		5
		Решение. S = ò					t 3 dt =		t 4	= 78,125 м.
						2		8
		S	0							0
n ср.	=		=	78,125	= 15,625 м/с.
		T
			5