Математический анализ_ЗФО_1 курс

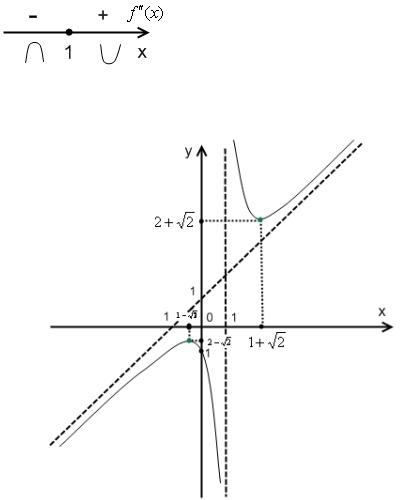
=	(x -	1)([2x - 2)(x -1)- (x 2 - 2x -1)× 2]			=	2x 2	- 2x - 2x + 2 - 2x 2 + 4x + 2	=	4	.
			(x -1)4				(x -1)3		(x -1)3
	4		¹ 0 , следовательно, точек перегиба нет.
(x -1)3

Исследуем направление выпуклости в окрестности точки x = 1:

6.ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ГРАФИКА ФУНКЦИИ НА ¥ И В

ОКРЕСТНОСТЯХ ОСОБЫХ ТОЧЕК.

Вычислим предел функции

при х ® +¥

	lim	x 2	+1	=	é+ ¥ù			= +¥
					ê		ú
		x	-1			+ ¥
	x®+¥				ë		û

Аналогично при х ® -¥ :

	lim	x 2	+1	=	é+ ¥ù			= -¥
					ê		ú
		x	-1			- ¥
	x®-¥				ë		û

В окрестности асимптоты х = 1 необходимо вычислить два предела: при х стремящемся к 1 справа (обозначают х ® 1 + и говорят, что х стремится к 1 оставаясь больше 1), и при х стремящемся к 1 слева (обозначают х ® 1 - и говорят, что х стремится к 1 оставаясь меньше 1):

1) lim

x 2

+1

= lim

2

= +¥

-1

x®1+ x

x®1+ x -1

2) lim

x 2

+1

= lim

2

= -¥

Рисунок 1.

-1

x®1- x

x®1+ x -1

Рассмотрим подробнее первый случай.

Т.к. х = 1 – вертикальная асимптота, то lim

x 2

+1

= ¥ . Нам необходимо

-1

x®1 x

знать знак этой бесконечности ( + ¥ или - ¥ ). Т.к. при подстановке х = 1 в функцию зануляется знаменатель, а в числителе получается число, то можно

записать lim	x 2	+1		= lim	2		.
		-1
x®1+ x				x®1+ x -1

Далее проводятся следующие рассуждения:

Т.к. х ® 1 + (т.е. х стремится к единице, но остается больше нее), то выражение х -1 ® 0 , причем будет больше нуля, потому что при вычитании из числа большего единицы числа равного единице, мы получим число положительное.

Таким образом, если 2 (положительное число) поделить на число очень маленькое, но положительное, получим очень большое положительное число (!),

т.е. + ¥	. Поэтому lim	x 2	+1		= lim	2		= +¥ .
			-1
	x®1+ x				x®1+ x -1

Аналогичные рассуждения проводятся и во втором случае. В итоге получим график, показанный на Рисунке1.

Функции нескольких переменных

Рассмотрим множество D, состоящее из пар действительных чисел(x, y), и

некоторое множество Z действительных чисел.

Если каждой паре действительных чисел(x; y)Î D по некоторому правилу f

поставлено в соответствие одно определенное действительное числоz Î Z , то говорят,

что на множестве D задана функция z = f (x, y) , принимающая значения из множества Z.

Функцию z = f (x, y) называют функцией двух переменных, а переменные x и y -

независимыми переменными или аргументами.

Множество D называется областью определения функции. Областью определения

функции двух переменных является множество точек плоскости.

Функцию	двух	переменных можно	задавать	аналитически, графически и
табличным способом.
Частное	значение	функции z = f (x, y) при	x = x0 ,	y = y0 обозначается через
z0 = f (x0 , y0 )

Геометрическим изображением (графиком) функции двух переменных z = f (x, y)

является, вообще говоря, поверхность в пространстве Oxyz.
Аналогично	определяется	функция	большего	числа переменных
z = f (x1 , х2 ,..., хn ) .

Частные производные функции многих переменных

Частной производной функции нескольких переменных по одной из этих

переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю.

Для функции двух переменныхz = f (x, y) , полагая, например, у постоянной,

получаем производную

¶z	= lim	f (x + Dx, y) - f (x, y)	= f x¢(x, y) ,
¶x Dx®0		Dx

которая называется частной производной функции z по переменной х. Аналогично определяется частная производная функции z по переменной у

¶z	= lim	f (x, y + Dу) - f (x, y)	= f	у¢(x, y) .
¶у Dу®0		Dу

Полным приращением функции z = f (x, y) называется разность

Dz = f (x + Dx, y + Dy) - f (x, y)

Пример:

Вычислим частные производные функции u = x3 y 2 z + 4x - 5 y + 2z + 2 .

При вычислении частной производной

¶u

, переменные z

и y рассматриваются

¶u

¶x

как константы. Тогда

= 3x 2 y 2 z + 4 .

¶x

Аналогично, при вычислении

¶u

как константы рассматриваются переменные х и

¶y

z, и

¶u

= x3 2 yz - 5 .

¶у

И, наконец,

¶u

= x3 y 2 + 2 .

¶z

Частные производные высших порядков

Пусть дана

функция z = f (x, y) , имеющая частные

производные

¶z

и

¶z

.

¶x

¶y

Частные производные от этих производных называютсячастными производными 2-го

¶

æ

¶z ö

¶2 z

¶

æ

¶z ö

¶2 z

¶

æ

¶z ö

¶2 z

¶ æ

¶z ö

¶2 z

порядка и обозначаются:

ç

÷

=

,

ç

÷

=

,

ç

÷ =

,

ç

÷

=

.

2

2

¶x è ¶x ø ¶x

ç

÷

¶y

¶y

ç

÷

¶x¶y

¶y è

¶y ø

è ¶x ø ¶y¶x ¶x è

¶y ø

Аналогично определяются и обозначаются частные производные3-го порядка и

других высших порядков.

¶ æ ¶z

ö

¶2 z

¶

æ

¶z ö

¶2 z

Частные производные вида

ç

÷ =

и

ç

÷

=

называют

¶y è ¶x ø ¶y¶x

ç

÷

¶x¶y

¶x è

¶y ø

смешанными производными второго порядка.

Пример:

Найдем частные производные второго порядка функции z = arctg x . y

Найдем сначала частные производные первого порядка:

¶z

1

1

y

¶z

1

æ

x

ö

x

=

×

=

,

=

×

ç

-

÷

= -

.

¶x

æ x ö

2

y

y

2

+ x

2

¶y

æ x ö

2

ç

y

2

÷

y

2

+ x

2

è

ø

1 +

ç

÷

1 + ç

÷

ç

÷

ç

÷

è

y ø

è y ø

Теперь дифференцируем вторично:

¶2 z

¶

æ

¶z ö

¶

æ

y

ö

y

2xy

=

ç

÷

=

ç

÷ = -

× 2x = -

,

2

2

2

2

2

2

2

¶x

¶x

ç

+ y

÷

x

+ y

x

+ y

è ¶x ø ¶x è x

ø

¶2 z

¶

æ

¶z ö

¶

æ

x

ö

x

2xy

=

ç

÷

=

ç

-

÷

=

× 2 y =

,

2

2

2

2

¶y

¶y

ç

÷

¶y

ç

x

+ y

2 ÷

(x

è

¶y ø

è

ø

2 + y 2 )

(x 2 + y 2 )

¶2 z

¶

æ

¶z

ö

¶

æ

x

ö

(x 2

+ y 2 )- x × 2x

x 2

- y 2

=

ç

÷

=

ç

-

÷

= -

=

2

2

2

2

¶x¶y ¶x

ç

¶y

÷

¶x

ç

x

+ y

÷

(x 2

(x 2

è

ø

è

ø

+ y 2 )

+ y 2 )

2

æ

ö

2

2

2

2

¶ z

¶

æ ¶z

ö

¶

y

(x

+ y )- y × 2 y

x - y

ç

÷

=

ç

÷

=

2

2

=

2

=

2 .

¶y¶x

¶y

è

¶x

ø

¶y

è x

+ y

ø

(x 2

+ y 2 )

(x 2 + y 2 )

Экстремум функции нескольких переменных.

Определение:

Точка М 0 (х 0 , у0 ) называется точкой максимума (минимума) функции

z = f (x, y) , если существует такая окрестность точки М 0 , что для всех точек М (х, у)									из
этой окрестности,	отличных от	точки М 0 ,			выполняется			неравенство f (M ) < f (M	0 )
( f (M ) > f (M 0 ) ).	Точки максимума и				минимума			функции называютсяточками
экстремума этой функции.
Теорема (необходимое условие экстремума):
Если функция z = f (x, y)		в точке М 0 (х 0 , у0 ) имеет экстремум, то все её частные
производные первого порядка в этой точке (если они существуют) равны нулю, т.е.
			¶z	= 0 и		¶z	= 0 .
			¶x			¶у

Точки, в которых все частные производные первого порядка функцииz = f (x, y)

равны нулю или хотя бы одна из них не существует, называются критическими.

Аналогично определяются необходимые условия экстремума функции большего числа переменных.

Теорема (достаточное условие экстремума):

	Пусть А =	¶2 z	(х0 , у0 ) , В =		¶2 z	(х0 , у0 ) и С =	¶2 z	(х0 , у0 ) , а точка М	0 (х 0 , у	0 )
		¶x 2			¶x¶у		¶у 2
является критической точкой. Обозначим D = АС - В 2 . Тогда если D > 0 , то точка
М 0 (х 0 , у0 ) является точкой экстремума функции z = f (x, y) , причем
1.	Если А > 0 , то М 0 (х 0 , у0 )			– точка минимума функции z = f (x, y)
2.	Если А < 0 , то М 0 (х 0 , у0 )			– точка максимума функции z = f (x, y)

3.Если D < 0 , то в точке М 0 (х 0 , у0 ) экстремума нет.

4.Если D = 0 , то в точке М 0 (х 0 , у0 ) может быть экстремум, а может и не быть (требуются дополнительные исследования).

Пример 1. Исследовать на экстремум функцию z = x3 + 3xy 2 -15x -12 y .

Решение:

Найдем частные производные и составим систему уравнений:

¶z = 3x 2 + 3y 2 -15 ¶x

¶z = 6xy -12 ¶y

ì	2	+ y	2	- 5	= 0 Þ
íx
îxy - 2 = 0

¶z = 3x 2 + 3y 2 -15 = 0 ¶x

¶z = 6xy -12 = 0 ¶y

решив систему, получим четыре критические точки:

M1 (1; 2) , M 2 (2; 1) , M 3 (-1;-2) , M 4 (-2; -1) .

Найдем производные второго порядка A =

¶

2 z

= 6x , C =

¶2 z

= 6x , B

=

¶2 z

= 6 y и

¶x 2

¶y 2

¶x¶y

составим определитель D = АС - В 2

для каждой критической точки.

1)

Для точки M1 (1; 2) : A = 6, B = 12, C = 6 ,

D = АС - В 2

= 6 × 6 - (12)2

= 36 -144 < 0 .

Значит, в точке M1 (1; 2) экстремума нет.

2)

Для точки M 2 (2; 1) : A = 12, B = 6, C = 12 ,

D = АС - В 2 = 12 ×12 - (6)2 = 144 - 36 > 0 .

A = 12 > 0 . Значит в точке M 2 (2; 1)

функция

имеет минимум. Этот минимум равен значению функции при x = 2, y = 1, т.е.

zmin = 8 + 6 - 30 -12 = -28 .

3)

Для точки M 3 (-1;-2) : A = -6, B = -12, C = -6 ,

D = АС - В 2 = -6 ×(- 6)- (-12)2 = 36 -144 < 0 . Значит, в точке M 3 (-1;-2) экстремума нет.

4)

Для точки M 4 (-2; -1) :

A = -12, B = -6, C = -12 ,

D = АС - В 2 = -12 ×(-12)- (- 6)2

= 144 - 36 > 0 . A = -12 < 0 . Значит в точке M 4 (-2; -1)

функция имеет максимум. Этот максимум равен значению функции при x = -2, y = -1 ,

т.е. zmax

= -8 - 6 + 30 +12 = 28 .

Ответ: M 2 (2; 1) - точка минимума и zmin = -28 ,

M 4 (-2; -1) - точка максимума и zmax

= 28

Пример 2. Производятся два вида товаров, цены которых соответственно равны

40 и

20. Функция затрат, связанных

с

производством этих

товаров ,

имеет

вид

С(x,

y) = 0,2x 2 + 0,1xy + 0,3y 2 , где x и y

–

количества товаров первого и второго видов.

Требуется составить функцию прибыли, найти ее экстремумы

и проверить известное

правило

экономики: предельная

цена

товара

равна

предельным

издержкам на

производство этого товара.

Решение:

Составим функцию прибыли как разность дохода и затрат на производство:

z = 40x + 20 y - (0,2x 2 + 0,1xy + 0,3y 2 )= 40x + 20 y - 0,2x 2

- 0,1xy - 0,3y 2 . С экономической

точки зрения переменные x и y

должны быть неотрицательны.

Для нахождения критических точек сначала выпишем необходимое условие,

т.е.

найдем первые частные производные функции z и приравняем их к нулю.

¶z

= 40 - 0,4x - 0,1y = 0 ,

¶z

= 20 - 0,1x - 0,6 y = 0 . Решая систему уравнений

¶x

¶y

ì40 - 0,4x - 0,1y = 0

получим x =

2200

и y =

400

. Таким образом, имеем критическую

í

- 0,6 y = 0

î20 - 0,1x

23

23

æ

2200

400

ö

точку M ç

;

÷ . (Если бы оказалось,

что хотя бы одна из переменных приняла

23

23

è

ø

отрицательное значение, то задача с экономической точки зрения не имела бы решения.)

Проверим достаточное условие экстремума. Найдем вторые частные

производные A =

¶2 z

= -0,4

, C =

¶2 z

= -0,6 , B =

¶2 z

= -0,1. Далее,

¶x 2

¶y 2

¶x¶y

D =

АС - В

2

= -0,4 × (- 0,6)-

(-

0,1)

2

= 0,23 > 0 , A = -0,4 < 0 . Значит M

æ

2200

;

400 ö

-

ç

÷

23

23

è

ø

точка максимума.

Определим максимальное значение прибыли:

zmax

= 40 ×

2200

+ 20 ×

400

æ

2200 ö2

æ

2200 öæ 400

ö

æ

400 ö

2

48000

.

- 0,2ç

÷

- 0,1ç

֍

÷

- 0,3ç

÷

=

23

23

23

23

23

è

ø

è

23 øè

ø

è

23 ø

Вданном случае предельная цена товара х равна р1 = 40 , а товара у равна

р2 = 20 . Выражение «предельная цена товара равна предельным издержкам на

производство этого товара»

математически записывается в виде: p =

¶C(x, y)

,

1

¶x

p2

=

¶C(x, y)

, где М – точка экстремума.

M

¶y

M

В нашем случае

¶C(x, y)

= 0,4 ×

2200

+ 0,1×

400

= 40 = p ,

¶x

23

23

1

¶C(x, y)

2200

M

= 0,1×

+ 0,6 ×

400

= 20 = p2 .

¶y

M

23

23

Следовательно, известное правило экономики действительно выполняется.

Первообразная и неопределенный интеграл

Определение:

Непрерывная на интервале а;b функция F (x) называется первообразной функции f (x) , если F (x) дифференцируема и

F ¢(x) = f (x) .

Утверждение:

Если две функции являются первообразными для одной и той же функции f (x) , то они отличаются на константу.

Доказательство:

Действительно, т.к. производная константы (числа) равна нулю, то

(F (x) + C )¢ = f (x) .

Предположим, что F1 (x) + C1 и F2 (x) + C2 - первообразные для f (x) , тогда

(F1 (x) + C1 )¢ = [F1 (x)]¢ = f (x)

(F2 (x) + C2 )¢ = [F2 (x)]¢ = f (x)

А это и означает, что F1 (x) и F2 (x) отличаются только на число .

Таким образом, функция f (x) имеет бесконечно много первообразных, и все они отличаются только на константу.

Ч.т.д.

Определение:

Совокупность всех первообразных функции f (x) называется неопределенным интегралом функции f (x) и обозначается

ò f (x)dx = F (x) + C .

Функция f (x) называется подынтегральной функцией, f (x)dx – подынтегральным

выражением.

Из определения первообразной следует:

1. (ò f (x)dx)¢ = f (x)

Действительно, т.к.	ò f (x)dx = F (x) + C , то продифференцировав обе части,
¢	¢	¢
получим (ò f (x)dx) = (F (x) + C )		= F (x) = f (x) .
2. òF ¢(x)dx = F (x) + C
Действительно, т.к. F ¢(x) =		f (x) , то òF ¢(x)dx = ò f (x)dx =F (x) + C .

Свойства неопределенного интеграла:

1.Линейность (интеграл от линейной комбинации функций равен линейной комбинации интегралов от этих функций)

ò(af (x) + bg(x))dx = a ò f (x)dx + b ò g(x)dx

2.Формула интегрирования по частям:

òf (x)g ¢(x)dx = f (x)g(x) - ò f ¢(x)g(x)dx

3.Замена переменной в неопределенном интеграле:

òf (j(x))d (j(x)) = j(x) = u = ò f (u)du .

Таблица основных неопределенных интегралов

1.

ò xn ×dx =

xn+1

+ C ,

(n ¹ –1)

òU n × du =

U n+1

+ C , (n ¹ –1)

n +1

n +1

2.

òdx = x + C

òdU =U + C

3.

ò

dx

= ln

x

+ C

ò

dU

= ln

U

+ С

x

U

4.

òa xdx =

a x

+ C

òaU du =

aU

+ C

ln a

ln a

5.

òexdx = ex + C

òeU du = eU + C

6.

òsin xdx = -cos x + C

òsin udu = -cos u + C

7.

òcos xdx = sin x + C

òcos udu = sin u + C

8.

ò

dx

= tgx + C

ò

du

= tgu + C

cos2 x

cos2 u

9.

ò

dx

= -ctgx + C

ò

du

= -ctgu + C

sin 2 x

sin 2 u

10. òtgxdx = -ln

cos x

+ С

òtgudu = -ln

cosu

+ С

11. òсtgxdx = ln

sin x

+ С

òсtgudu = ln

sin u

+ С

12. ò

dx

= ln

tg

x

+ C

ò

du

= ln

tg

u

+ C

sin 2 x

2

sin 2 u

2

ì1

arctg

x

+ С

ì1

arctg

u

+ C

dx

ï

du

ï

ï

ï

13. ò

=ía

1

a

x

ò

=

ía

1

a

u

a

2

+ x

2

a

2

+ u

2

ï

+ С

ï

+ C

ï-

a

arcсrc

a

ï-

a

arcctg

a

î

î

14. ò

dx

=

1

ln

x - a

+ C

ò

du

=

1

ln

u - a

+ C

x

2 - a2

x + a

u

2 - a2

u + a

2a

2a

15. ò

dx

=

1

ln

x + a

+ C

ò

du

=

1

ln

u + a

+ C

a

2

х

2

x - a

a

2

2

-

2a

- u

2a

u - a

ì

x

+ С

ì

u

+ C

dx

ïarcsin

a

du

ïarcsin

a

16.

=

ï

ï

ò a 2 - x 2

í

x

ò a 2 - u 2

= í

u

ï

+ C

ï

+ C

ï- arccos

a

ï- arccos

a

î

î

17. ò

dx

= ln x +

x2 + a + C

ò

du

= ln u +

u2 + a + C

x2 + a

u2 + a