Математический анализ_ЗФО_1 курс

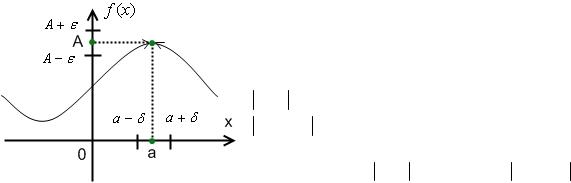
Предел функции

Определение:

Пусть даны два множества X и Y. Если каждому элементу x Î X соответствует один элемент y ÎY , то, говорят, что задана функция с областью определения X и областью значений, лежащих в Y.

f : X ® Y .

Определение:

Функция f называется возрастающей (на множестве X), если для любых x1 , x2 Î X

таких, что при x1 > x2 f (x1 ) ³ f (x2 ) .

Функция называется строго возрастающей, если при x1 > x2 f (x1 ) > f (x2 ) .

f ­: " x1 , x2 Î X : x1 > x2 Þ f (x1 ) ³ f (x2 ) .

Определение:

Функция f называется убывающей (на множестве X), если для любых x1 , x2 Î X

таких, что при x1 > x2 f (x1 ) £ f (x2 ) .

Функция называется строго возрастающей, если при x1 > x2 f (x1 ) < f (x2 ) .

f ¯: " x1 , x2 Î X : x1 > x2 Þ f (x1 ) £ f (x2 ) .

Определение:

Функция f называется невозрастающей на множестве X, если существует x1 > x2

такой, что f (x1 ) < f (x2 ) .

Функция f называется неубывающей на множестве X, если существует x1 < x2

такой, что f (x1 ) > f (x2 ) .

Определение:

Функция называется монотонной, если она либо возрастает, либо убывает.

Определение:

Число А называется пределом функции f (x) в точке а, если эта функция определена в некоторой окрестности точки а за исключением, быть может, самой точки а, и для каждого e > 0 существует d > 0 такое, что для всех х, удовлетворяющих условию

x - a < d , x ¹ a выполняется неравенство f (x) - A < e .

" e > 0 $d > 0 : x - a < d , x ¹ a Þ f (x) - A < e .

Свойства предела:

Теорема:

Пусть f : X ® R , g : X ® R – две функции с общей областью определения X.

Если существует lim f (x) = A				и lim g(x) = B для всех x Î X , то
		x®a		x®a
1.	lim(af (x) + bg(x)) = a lim f (x) + b lim g(x) = a × A + b × B
	x®a		x®a	x®a
2.	lim(f (x) × g(x))= lim f (x) ×lim g(x) = A × B
	x®a	x®a	x®a
	Если g(x) ¹ 0,	x Î X	и lim g(x) = B ¹ 0 , то lim		f (x)		lim f (x)		A
3.						=	x®a	=
							lim g(x)		B
			x®a	x®a g(x)

x®a

x®2 (

4x2

)

Пример 1. Найти lim

- 6x +1

Решение:

)

lim

(

= lim 4x2 - lim 6x + lim1 = 4 lim x2 - 6 lim x + lim1 =

4x2 - 6x +1

x®2

x®2

x®2

x®2

x®2

x®2

x®2

= 4 ×22 - 6 ×2 +1 =16 -12 +1 = 5

или

)

x®2 (

= 4 ×22 - 6

×2 +1 =16 -12 +1 = 5 .

lim

4x2 - 6x +1

Пример 2. Найти lim

x2

- 4

Решение. При

x®2 x2 -5x + 6

x = 2 числитель и знаменатель данной функции обращается в нуль.

Получена

неопределенность

0

, которую

нужно

раскрыть .

Разложим числитель и

0

знаменатель на линейные множители

x2 -

4

é0 ù

(x

- 2)(x + 2)

(x + 2)

2 + 2

lim

=

ê

ú = lim

(x

- 2)(x - 3)

= lim

(x - 3)

=

=

2

2 -3

x®2 x

-5x + 6

ë0

û x®2

x®2

=	4	= -4
	-1
		Числитель разложили по формуле сокращенного умножения a2 - b2 = (a -b)(a + b),
знаменатель – используя формулу разложения квадратного трехчлена на множители :
ax2 + bx + c = a (x - x1 )(x - x2 ) , где x1,				x2 - корни уравнения ax2 + bx + c = 0
		Пример 3. Найти предел lim	x 3	+ 7 x 2 + 16 x + 12
					.
		x®-2		x 3 + 3x 2 - 4

Решение. При x = -2 многочлены в числителе и знаменателе исходного выражения обращаются в нуль, следовательно, их пределы в точке x = -2 равны нулю и мы имеем

0

неопределённость вида 0 . Преобразуем исходное выражение. Разложим многочлены в

его числителе и знаменателе на множители, воспользовавшись тем, что x = 2 является их корнем, с помощью группировки слагаемых или разделив их на х - 2 :

_ x3 + 7x 2 +16x +12

x + 2

_ x3 + 3x 2 - 4

x + 2

x3 + 2x 2

x 2 + 5x + 6

x3 + 2x 2

x 2 + x - 2

_ 5x 2 +16x

_ x 2 - 4

5x 2 +10x

x 2 + 2x

_ 6x +12

_ - 2x - 4

6x +12

- 2x - 4

0

(x2 +5x +

,

0

.

lim

6)(x + 2)

= lim

x2

+5x + 6

(x2 + x - 2)(x + 2)

Получаем x®-2

x®-2 x2 + x - 2 .

Мы снова имеем неопределённость, так как при х = 2 числитель и знаменатель последней дроби обращаются в нуль. Разлагаем их на множители, сокращаем и находим

искомый предел:	lim	(x + 2)(x +3)	= lim	x +3		= -	1	.
	x®-2 (x + 2)(x -1) x®-2 x -1					3

Пример 4. Найти предел lim

x2

+ x -

2x + 2

x2 -3x + 2

.

x®2

0

Решение. Имеем неопределённость вида

. Преобразуем исходное выражение,

0

умножив его числитель и знаменатель на множитель

x 2

+ x +

2x + 2 , сопряжённый к

числителю.

lim

(

x2 + x - 2x + 2)( x2 + x + 2x + 2)

= lim

x2 - x - 2

.

(x2 -3x + 2)( x2 + x + 2x + 2)

x®2

(x2 -3x + 2)( x2 + x + 2x + 2)

x®2

Поскольку

lim(

x2 + x +

2x + 2)= 2

6 , то

x®2

1

lim

x2 - x - 2

=

1

lim

(x

- 2)(x +1)

=

1

lim

x +1

=

3

.

2 6

2 6 x®2 x2 - 3x + 2

2

6 x®2 (x - 2)(x -1)

2 6 x®2 x -1

Понятие бесконечно малых функций. Их применение к нахождению пределов.

Определение:

Функцию f : X ® R называют бесконечно малой при х ® а , если lim f (x) = 0 ,

x®a

x Î X .

Определение:

Функции f : X ® R и g : X ® R называются эквивалентными при х ® а , x Î X ,

если lim f (x) = 1 .

x®a g(x)

При вычислении пределов удобно пользоваться заменой бесконечно малых на эквивалентные. Если f – бесконечно малая при х ® а , то справедливо:

sin[ f (x)]			эквивалентна	f (x)
tg[ f (x)]			эквивалентна	f (x)
arcsin[ f (x)]			эквивалентна	f (x)
arctg[ f (x)]			эквивалентна	f (x)
cos[ f (x)]			эквивалентна	1 -	f 2 (x)
				2
ln[1 + f (x)]			эквивалентна	f (x)
a f ( x) -1			эквивалентна	f (x) × ln a
e f ( x)			эквивалентна	1 + f (x)
[1 + f (x)]p			эквивалентна	1 + p × f (x)
	1		эквивалентна	1 + f (x)
[1+ f (x)]p
						p

Пример 1.	lim	sin 2x		= lim		2x		=	2
	x®0 arctg3x			x®0 3x 3
Пример 2.	lim	sin 5x	= lim		5x		= 5

x®0 x

x®0 x

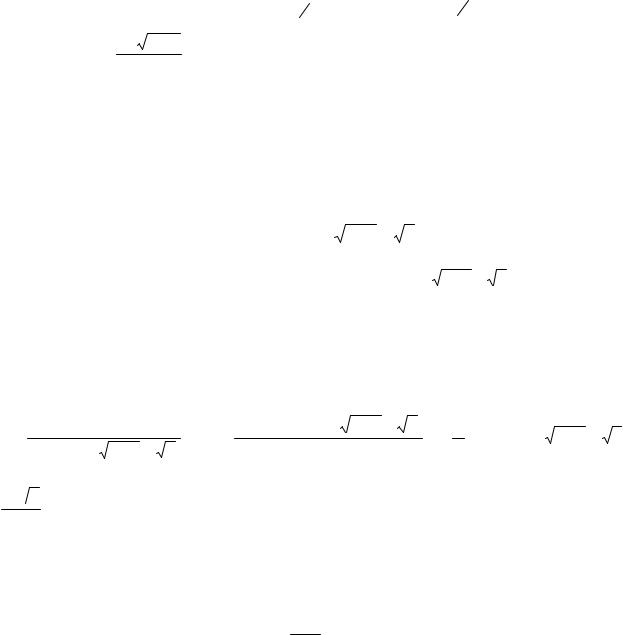
æ

x

2

ö

æ

(3x)

2

ö

ç

-

÷

ç

÷

2

cos x - cos 3x

ç1

2

÷ -

ç1 -

2

÷

4x

Пример 3. lim

= lim

è

ø

è

ø

= lim

= 4

x 2

x 2

x®0

x®0

x®0 x 2

1

æ

x 2

1

æ

æ

x 2

ö

ö 2

ö 2

1 -

ç1

-

÷

1

- ç1

+ ç

-

÷

÷

1 - cos x

ç

2

÷

ç

ç

2

÷

÷

Пример 4. lim

= lim

è

ø

= lim

è

è

ø

ø

=

1 - cos x

æ

x

2 ö

x 2

x®0

x®0

x®0

1 -

ç

÷

ç1 -

÷

2

è

2 ø

æ

x

2

ö

1 -

ç

÷

2

ç1 -

4

÷

2x

1

= lim

è

ø

= lim

=

.

x 2

2

2

x®0

x®0 4x

2

Пример 5. Вычислить предел lim

arcsin(x3 - 3x 2 )ln(x 2 - 2x - 2)

.

sin px(

x -1 -

2 )

x®3

Решение. Заметив, что все сомножители в числителе и знаменателе исходного

выражения есть бесконечно малые при x ® 3 , заменим их, кроме

x -1 -

2 , на

эквивалентные:

arcsin(x3 - 3x2 )~ x3 - 3x2 ,

ln(x2 - 2x - 2)= ln((x2 - 2x - 3)+1)~ x2 - 2x - 3,

sinpx = sin(p ( x - 3) + 3p ) = -sin(p (x - 3)) ~ -p (x - 3)

Получаем:

= -lim x(x - 3)2 (x +1)(

2 )= - 1 lim x(x +1)(

a = lim (x3 - 3x2 )(x 2 - 2x - 3)

x -1 +

x -1 + 2 )=

x®3 -p (x - 3)( x -1 - 2 )

x®3

p (x - 3)(x -1 - 2)

p x®3

= - 72 2

p.

Первый и второй замечательные пределы

Первый замечательный предел имеет вид:

lim sin x = 1

x®0 x

Следствия первого замечательного предела:

1.

lim

x

= lim

1

=

1

= 1

x®0 sin x

x®0 sin x

1

sin (kx)

x

2.

lim

= lim

sin t

= 1

x®0

kx

t ®0

t

3.

lim

kx

= lim

1

=

1

= 1

sin( kx)

x®0

sin(kx) x®0

1

kx

Второй замечательный предел имеет вид:

æ

1 öx

= e

lim

ç1

+

÷

x®¥è

x ø

1

lim(1 + x)

= e

x

x®0

Следствия из второго замечательного предела:

æ

a öx

a

lim

ç1 +

÷ = e

,

x®¥è

x ø

a

lim(1 + x)

= ea .

x

x®0

Пример 1. Найти lim

sin3x

2x

x®0

Решение. lim

sin 3x

= lim

sin 3x

= lim

3

sin 3x

=

3

×1 =

3

.

2 ×3x

x®0

2x

x®0

x®0 2 3x

2

2

3

Пример 2. Найти lim

3x2

.

x®0 1- cos(2x)

Решение. По используя тригонометрическую формулу sin 2

x =

1 - cos 2x

(формула

понижения степени) заменим 1 - cos 2x = 2 sin 2

x , получим:

2

lim

3x 2

= lim

3x 2

=

3

lim

x2

=

3

lim

æ x

×

x

ö

=

ç

÷

x

sin x

x®0 1 - cos(2x)

x®0 2 sin 2 x

2 x®0 sin 2

2 x®0è sin x

ø

=

3

lim

x

× lim

x

=

3

.

2 x®0 sin x

x®0 sin x

2

æ

2

x2 +1

Пример 3. Найти lim

ö

4

ç1

-

÷ .

x2 +1

x®¥è

ø

Решение.

Мы

имеем

неопределенность вида 1¥ .

Значит, приведем

выражение к

æ

1

ö

и

– т.е сведем ко второму замечательному пределу:

виду ç1

+

÷

и

è

ø

æ

2 ö

x2 +1

æ

æ

2

ö

ö

x2 +1

4

4

limç1

-

÷

= limç1 +

ç-

÷

÷

=

2

2

x®¥è

x

+1ø

ç

è x

+1ø

÷

x®¥è

ø

2

2

æ

2

ö

x +1

1

x +1

1

Т.к.

=

×

= -

ç

x +1

÷

4

2

2

2

×ç-

2

÷ , то продолжим равенство

è

ø

x2

+1

æ

1 ö

æ

æ

2

öö

-

×ç -

÷

2

è

2 ø

= {x

= lim ç1 + ç

-

÷÷

2

ç

è

x

+1

÷

x®¥è

øø

æ

и ö-

1

2

æ

1 ö

2

=

-

= и

= limç

ç1

+

÷

÷

2

х

+1

и®¥ç

è

и ø

÷

è

ø

æ x + 3 öx

Пример 4. Найти lim ç ÷ x®¥ è x - 2 ø

Решение:

æ

x2 +1

× ö-

1

æ

2 öö

-

2

a×b

= (x

a b

)} = lim

çæ

2 ÷

ççç1

+ ç

-

÷÷÷

÷

= .

x

2

+1

x®¥çè

è

øø

÷

è

ø

-1

=e 2 .

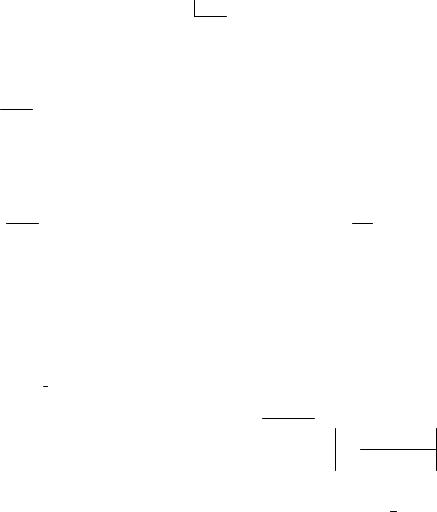
В данном случае снова имеем неопределенность вида1¥ . Выделим целую часть и сведем ко второму замечательному пределу:

x + 3 x - 2

x - 2 1

5

æ x + 3 öx lim ç ÷ x®¥ è x - 2 ø

5

×x

éæ

x-

2

ù

æ

5

öx

5

ö

x-2

lim

5 x

5

= lim

ç1

+

÷

=lim

êç1

+

÷

ú

= ex®¥ x-2 = e5

x - 2

x - 2

x®¥ è

ø

x®¥

êè

ø

ú

ë

û

1442443

e

или разделим числитель и знаменатель на x

æ x + 3 öx lim ç ÷ x®¥ è x - 2 ø

		æ	1+		3		öx
		ç				÷
	= lim				x
		ç					÷
	x®¥	ç	1-		2	÷
		è			x ø

=lim

x®¥

æ	+	3	öx
ç1			÷
		x
è			ø	=
æ	-	2	öx
ç1			÷
		x
è			ø

		æ	+	3	öx
	lim	ç1			÷
				x
	x®¥ è				ø
		æ	-	2	öx
	lim	ç1			÷
				x
	x®¥ è				ø

= e3 = e5 . e-2

			1
æ			2 ö
					x sin 3 x
Пример 5. Вычислить предел функции limç	3	-		÷		.
x®0 è			cos x ø

Решение. Находим пределы основания и показателя степени исходного выражения и убеждаемся в том, что перед нами неопределённость вида 1¥. Выделяем в исходном

1

выражении формулу (1 + t t), t ® 0, и вычисляем предел.

1

æ

cos x

æ

2 ö x sin 3x

çæ

2(cos x -1)ö2(cos x-1)

a = limç1 + 2

-

÷

= limçç1 +

÷

cos x

x®0è

cos x ø

x®0çè

ø

è

1

2(cos -1)

1

2(cos -1)

-

= limçæ(1 + t

)÷ö x sin 3x cos x = limçæ

(1+ t

)÷ö x sin 3x

= lim e

t

t

x®0è

ø

x®0 è

ø

x®0

2(cos -1)

ö x sin 3x cos x

÷

÷ = t =

÷

ø

4 sin	2 x				-x2
		2		= lim e
x×3x					3x2
				x®0

2(cos x -1) = cos x

-1

=e 3 .

Производная функции. Основные определения

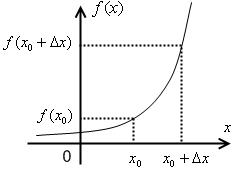
Пусть задана некоторая функция f : X ® R и х – ее аргумент. Dх называют приращением аргумента функции.

При переходе от х0 к х0 + Dх значение функции изменяется от f (x0 ) к f (x0 + Dx) соответственно.

Разность f (x0 + Dx) - f (x0 ) = Df (x) называют приращением функции.

Определение:

f (x) определена на промежутке (a; b) и x0 , x0

+ Dx Î (a; b) .

Пусть функция

Производной функции f (x) в точке х0 называется предел отношения

приращения функции к приращению аргумента при Dх ® 0

f ¢(x0 ) = lim

f (x0

+ Dx) - f (x0 )

,

Dx®0

Dx

если он существует и конечен!

Определение:

Функцию f (x)

называют дифференцируемой в точке х0 , если она имеет в ней

конечную производную.

Если f (x)

дифференцируема в каждой точке промежутка (a; b) , то

f (x)

называют дифференцируемой на этом промежутке.

Пример. Найти производную функции

f (x) = sin 2x в точке x0

=

p

по

определению.

6

sin (2(x0 + Dx))- sin 2x0

¢

(sin 2x0 )

= lim

=

Dx

Dx®0

2 sin (2(x0

+ Dx))- 2x0 ×cos

(2(x0 + Dx))+ 2x0

sin

(Dx

)×cos(2x0

+ Dx)

= lim

2

2

= 2 lim

=

Dx

Dx

Dx®0

(Dx )

Dx®0

sin

æ

p

ö

= 2 lim

× cos(2x0 + Dx) = 2 lim cos(2x0

+ Dx)= 2 cos(2x0

+ 0) = 2 cosç2

×

÷

= 1.

6

Dx®0

Dx

Dx®0

è

ø

Правила дифференцирования

Пусть заданы функции							f : X ® R и g : X ® R , дифференцируемые во множестве
Х. Тогда справедливы равенства:
1.			¢				¢			C Î R
	(С × f (x)) = C × f						(x),
2.					¢		¢		¢
	(f (x) ± g(x))					=	f (x)		± g (x)
3.			¢				¢			¢
	(f (x) × g(x))					= f (x)g(x) +				f (x) × g (x)
	æ	f (x)	ö¢	f	¢					¢
4.	ç		÷ =			(x)g(x) - f (x)g (x)
								2
	ç		÷				g		(x)
	è g(x)		ø

Доказательство:

¢

Cf (x + Dx) - Cf (x)

f (x + Dx) - f (x)

¢

1.

(С × f (x))

= lim

= C lim

= C × f (x)

Dx

Dx

Dx®0

Dx®0

(f (x) ± g(x))¢ = lim [f (x + Dx) ± g(x + Dx)]- [f (x) ± g(x)] =

Dx®0

Dx

2.

= lim

f (x + Dx) ± g(x + Dx) - (f (x) ± g(x))

= lim

f (x + Dx) - f (x) ± g(x + Dx) - (± g(x))

=

Dx®0

Dx

Dx®0

Dx

f (x + Dx) - f (x)

g(x + Dx)

- g(x)

¢

¢

= lim

±

=

f (x)

± g

(x).

Dx

Dx

Dx®0

3.

(f (x) × g(x))¢ = lim

f (x + Dx)g(x + Dx) - f (x)g(x)

=

Dx®0

Dx

Заметим, что f (x) + Df (x) = f (x) + f (x + Dx) - f (x) , и аналогично с функцией

g(x) : g(x) + Dg(x) = g(x) + g(x + Dx) - g(x) . Тогда продолжим равенство:

lim

(f (x) + Df (x))(g(x) + Dg(x))- f (x)g(x)

=

Dx®0

Dx

= lim

f (x)g(x) + Df (x)g(x) + f (x)Dg(x) + Df (x)Dg(x) - f (x)g(x)

=

Dx®0

Dx

lim

Df (x)g(x) + f (x)Dg(x) + Df (x)Dg(x)

= lim

Df (x)g(x)

+ lim

f (x)Dg(x)

+ lim

Df (x)Dg(x)

=

Dx®0

Dx

Dx®0

Dx

Dx®0

Dx

Dx®0

Dx

g(x) lim

Df (x)

+ f (x) lim

Dg(x)

Df (x)

¢

¢

+ lim

× lim Dg(x) = g(x) f

( x) + f (x)g (x)

Dx®0 Dx

Dx®0

Dx Dx®0 Dx Dx®0

Т.к. Dg(x) = g(x + Dx) - g(x) , то при Dx ® 0 следует g(x + Dx) ® g(x) , тогда Dg(x) = g(x + Dx) - g(x) ® g(x) - g(x) = 0 . Следовательно третье слагаемое в

нашем равенстве lim Df (x) × lim Dg(x) = f ¢(x) × 0 = 0 .

Dx®0 Dx Dx®0

			¢		f (x + Dx)	-	f (x)
æ		ö
	f (x)				g(x + Dx) g(x)				f (x + Dx)g(x) - f (x)g(x + Dx)
4. ç		÷	= lim					= lim		=
è g(x)		ø	Dx®0		Dx			Dx®0	g(x + Dx)g(x)Dx
ç		÷

Т.к. Dx ® 0 , то g(x + Dx) ® g(x) , продолжая равенство, получим:

= lim ( f (x) + Df (x))g(x) - (g(x) + Dg(x))f (x) =

Dx®0

g 2 (x)Dx

1

lim

f (x)g(x) + Df (x)g(x) - f (x)g(x) - f (x)Dg(x)

=

g 2 (x) Dx®0

Dx

1

é

Df (x)g(x) - f (x)Dg(x) ù

1

é

Df (x)g(x)

f (x)Dg(x) ù

=

êlim

ú

=

êlim

- lim

ú

=

g

2

Dx

g

2

Dx

Dx

(x) ëDx®0

û

(x) ëDx®0

Dx®0

û

1

¢

¢

f

¢

¢

(x)g(x) - f

(x)g (x)

=

[f

(x)g(x) - f (x)g (x)]=

.

g 2 (x)

g 2 (x)

Таблица производных

С¢ = 0

¢

= cos x

(Х n

¢ )= n × X n-1

(sin x)

(cos x)¢ = -sin x

(a x

¢ )= a x × ln a

(tgx)¢ =

1

(e x

¢)= e x

cos2 x

(ctgx)¢ = -

1

2 x

(log a x)¢ =

1

sin

1

x

× ln a

(arcsin x)¢ =

(ln x ¢)=

1

1 - x2

1

x

(arccos x)¢ = -

(arctgx)¢ =

1

1 - x2

1

1 + x 2

(arcctgx)¢ = -

1 + x 2

Пример 1. Найти производную функции y = 3x5 + 6x7 − 8х3 + x2 − 12 в точке x0 = –1.

Решение.

y' = 3(x5)' + 6(x7)' − 8(х3)' + (x2)' − (12)' = 15x4 + 42x6 − 24х2 + 2x.

Тогда производная функции в точке x0 = –1:

y'(–1) = 15(–1)4 + 42(–1)6 − 24(–1)2 +2(−1) = 15 + 42 – 24 − 2 = 31.

Пример 2. Найти производную функции y =																			1				-		2					+	3			в точке x0 = 1.
														5						x3				3		x5					x
Решение. Преобразуем функцию:
								1			2		3	-					3					-		5
				y =					-			+			= x 5 - 2x 3 + 3x-1.
													x
							5 x3 3 x5
Тогда
æ	-	3	ö¢ æ	-	5		ö¢							-				3		-1				æ				5		-		5		-1	ö
y¢ = ç x	5		÷ -ç	2x 3			÷ + (3x-1 )¢					= -			3	x 5						- 2		ç		-				x 3					÷	+ 3(-x-1-1 ) =
è			ø è				ø							5										è	3										ø

																								3								8									10				8
																	= -												x-					+										x-				-3x-2 .
																																5															3
																						5																3
Производная функции в точке x0 = 1:
			¢											3		-	8					10										-			8										-2													3				10													4
																	5																	3
		y (1)						== -								×1			+											×1								- 3×1											= -											+									- 3		= -							.
														5												3																																5				3
																																																																								15
																																													33								-5							6
Пример 3. Найти производную функции																																									y =									x												x						в точке x0 = 1.
																																																								x3
Решение. Преобразуем функцию
			3							6							3																	6															1 -3													1 - 3										- 7							- 4
		3				x - 5							x								x																			x																																									.
y =															= 3													-5															= 3x							3				2			- 5x								6			2		= 3x			6			- 5x				3
								x3												x3																		x3
Тогда
æ	-			7				-			4		ö¢						æ							7				ö				-			7			-1					æ							4				ö				-	4			-1							7	-				13			20			-	7
y¢ = ç	3x 6 -							5x 3					÷ = 3×						ç		-										÷ x 6												-		5ç			-									÷ x 3											= -				x 6 +										x 3 .
																										6																										3																			2								3
è													ø						è											ø															è											ø

Производная функции в точке x0 = 1:

y¢(1) = - 7 + 20 = 19 . 2 3 6

Пример 4. Найти производную функции у = 4х3 sin x в точке x0 = π/2.

Решение. Воспользуемся правилом нахождения производной произведения двух

функций:

¢

=

¢

¢

(f (x) × g(x))

f (x)g(x) +

f (x) × g (x) .

Тогда

¢

(

3

¢

(

3

¢

)

3

¢

2

3

y =

4х

sin x

)

=

4

x

= 4 ×3x sin x + 4х

cos x =

sin x + 4х (sin x)

=12x2 sin x + 4х3 cos x.

Производная функции в точке x0 = π/2:

y¢

æ p ö

æ p ö2

p

æ p ö3

p

p 2

p 3

2

ç

÷

=12

ç

÷

sin

+ 4

ç

÷ cos

=12 ×

×1+ 4 ×

×0 = 3p

.

2

2

4

8

è

2 ø

è

2 ø

è

2 ø

Пример 5. Найти производную функции y = (x + 8)ctg x в точке x0 = π/4.

Решение. Воспользуемся правилом нахождения производной произведения двух

функций:

(f (x) × g(x))¢ = f ¢(x)g(x) + f (x) × g ¢(x) .

Тогда