Темы вопросов

31. Свойства вероятностей. Условные вероятности. 2

32. Вероятность суммы. Формулы полной вероятности. 4

33. Формула Байеса. Независимые испытания. Схема Бернулли. Формула Бернулли. 5

34. Предельные теоремы в схеме Бернулли. 6

35. Математическое ожидание дискретной случайной величины. 8

36. Дисперсия дискретной случайной величины. 9

37. Непрерывная случайная величина. Интегральная и дифференциальная функция распределения. 10

38. Математическое ожидание и дисперсия непрерывной случайной величины. 12

39. Законы распределения случайных величин. 13

40. Генеральная совокупность и выборка. 16

31. Свойства вероятностей. Условные вероятности.

Для классического, статистического и геометрического определений вероятности выполняются следующие аксиомы:

1. для любого наблюдаемого события A.

2. 

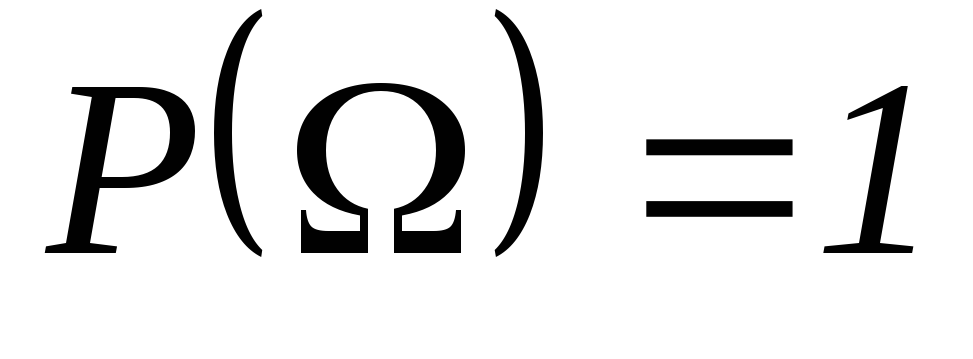
3. Если события A и B несовместны ( ), то .

Из аксиом можно вывести следующие свойства:

1. P() = 0, откуда следует, что если A и B несовместимы ( ), .

2. .

3. .

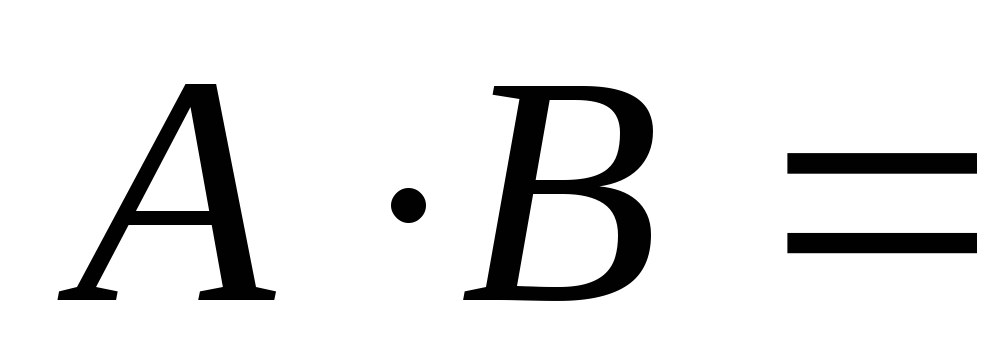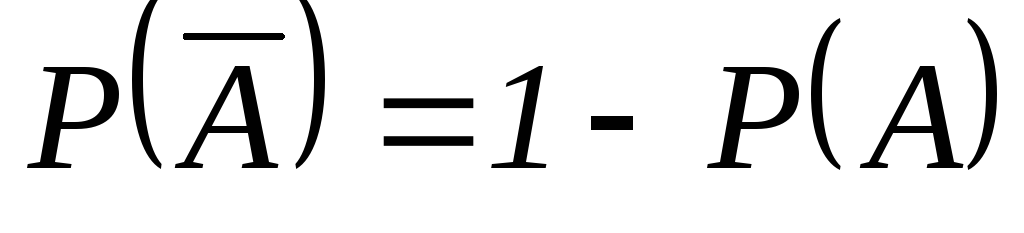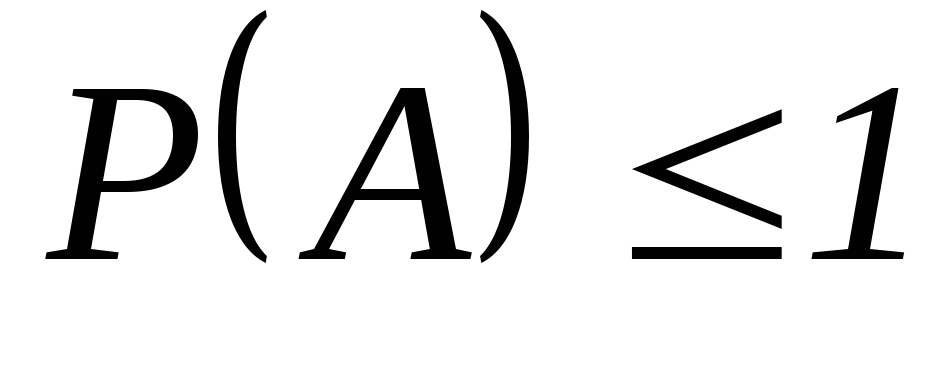4. Если (A влечет за собой B, т.е. все исходы, содержащиеся в A, содержатся и в B), то .

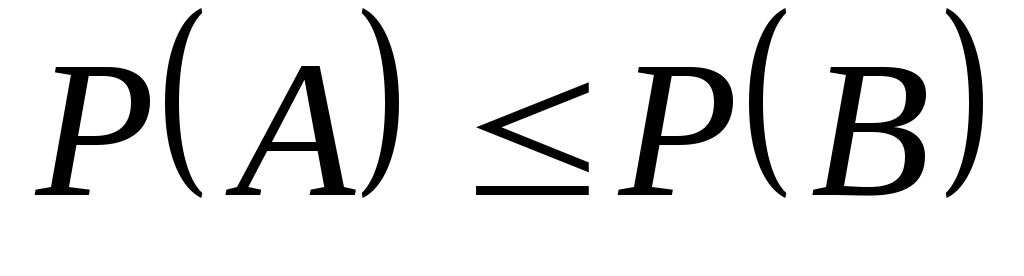5. Если A = B (т.е. и ), то .

6. - формула сложения вероятностей. В частности, если A и B несовместны ( ), то получим аксиому 3.

Условные вероятности. Независимость событий.

Пусть A и B – два события, рассматриваемые в опыте. Наступление одного события может влиять на возможность наступления другого.

Определение. Условной вероятностью события B при условии, что произошло событие A, называется отношение вероятности произведения этих событий к вероятности события A. Подчеркнем, что событие A уже произошло и .

(1)

Вероятность называется безусловной вероятностью.

Аналогично определяется условная вероятность .

Вероятность произведения событий.

Из определения условной вероятности следует, что

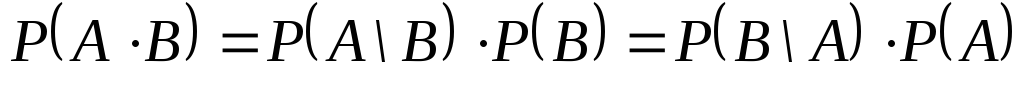(2),

т.е. вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.

Это равенство называют правилом или теоремой умножения вероятностей. Это правило обобщается на случай из n событий:

.

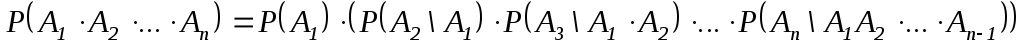Определение. Событие A называется независимым от события B, если его условная вероятность равна безусловной.

Лемма. О взаимной независимости.

Если событие A не зависит от события B, то и B не зависит от события A.

Два события называются независимыми, если появление одного из них не меняет вероятность появления другого.

События называются независимыми, если каждое из них не зависит от произведения любого числа остальных событий и от каждого в отдельности. В противном случае события называются зависимыми.

32. Вероятность суммы. Формулы полной вероятности.

Теорема. Вероятность суммы двух несовместимых событий A и B равна сумме вероятностей этих событий:

(1)

Следствие. Сумма вероятностей противоположных событий равна единице:

Теорема. Вероятность суммы двух совместимых событий A и B равна сумме вероятностей этих событий минус вероятность их произведения

(2)

Доказательство. Пусть из всего числа n элементарных событий k благоприятствуют событию A, l – событию B и m – одновременно событиям A и B. Отсюда событию A + B благоприятствует k + l – m элементарных событий. Тогда

Формула полной вероятности.

Теорема. Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместимых событий , образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:

(3)

Доказательство. Событие A может насупить лишь при условии наступления одного из событий , т.е. , причем ввиду несовместимости событий события также несовместимы. Поэтому на основании теорем сложения и умножения вероятностей имеем

Примеры.

1. В посевах пшеницы на делянке имеется 95% здоровых растений. Выбирают два растения. Определить вероятность того, что среди них хотя бы одно окажется здоровым.

Введем обозначения событий:

- первое растение здорово, - второе растение здорово, - хотя бы одно растение здорово.

Так как события и совместимые, то согласно формуле (2) имеем

2. Имеются три одинаковых по виду ящика. В первом находятся две белые мыши и одна серая, во втором – три белые и одна серая, в третьем – две белые и две серые мыши. Какова вероятность того, что из наугад выбранного ящика будет извлечена белая мышь?

Введем обозначения: - выбор первого ящика, - выбор второго ящика, - выбор третьего ящика, - извлечение белой мыши.

Так как все ящики одинаковы, то . Если выбран первый ящик, то . Аналогично , . Наконец, по формуле (3) получаем