4. Числовые характеристики функций случайных величин

Числовые характеристики функции Y = j(X) одного случайного аргумента X определяются по формулам:

-начальные моменты

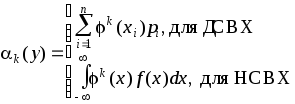; (4.1)

-математическое ожидание

m_y = a₁(y); (4.2)

-центральные моменты

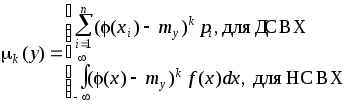; (4.3)

-дисперсия

D_y = m₂(y) = a₂(y) - . (4.4)

Числовые характеристики функции Y = j(X₁, X₂) двух случайных непрерывных величин X₁ и X₂, имеющих совместную плотность f(x₁, x₂), определяются по формулам:

-начальные моменты

; (4.5)

-центральные моменты

. (4.6)

В случае, когда закон распределения аргументов X₁ и X₂ неизвестен, а известны только их числовые характеристики m₁, m₂, D₁, D₂, K₁₂, то математическое ожидание m_y и дисперсию D_y величины Y = a₁X₁ + a₂X₂, где a₁, a₂ - константы, могут быть определены по формулам:

m_y = a₁m₁ + a₂m₂, (4.7)

. (4.8)

Если Y = X₁X₂, то

m_y = m₁m₂ + K₁₂. (4.9)

В случае независимых сомножителей X₁ и X₂ дисперсия Y может быть определена по формуле

. (4.11)

Пример 4.1 Случайная величина X равномерно распределена от -1 до +1. Определить математическое ожидание и дисперсию величины Y = X². Вычислить корреляционный момент величин X и Y.

Решение. Плотность вероятности X равна:

.

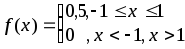Вычислим математическое ожидание Y по формуле (4.2):

.

Дисперсию D_y рассчитаем по формуле (4.4):

.

Вычислим корреляционный момент K_xy по формуле (2.5):

K_xy = M[XY] - m_xm_y = M[X×X²] - m_xm_y =M[X³] - m_xm_y.

Так как m_x = (a + b)/2 = (-1 + 1)/2 = 0, то

Пример 4.2. Величины X₁, X₂, X₃ независимы и имеют следующие числовые характеристики:

m₁ = 2, m₂ = -3, m₃ = 0, D₁ = 4, D₂ = 13, D₃ = 9.

Определить коэффициент корреляции r_zy величин Y и Z:

Y = 3X₁ - X₂,

Z = X₃ - 2X₁.

Решение. Вычислим математические ожидания Y и Z по формуле (4.7):

m_y = 3×m₁ - 1×m₂ = 9,

m_z = m₃ - 2×m₁ = -4.

Вычислим дисперсию D_y и D_z по формуле (4.8):

D_y = (3)²×D₁ + (-1)²×D₂ = 49,

D_z = D₃ + (-2)²D₁ = 25.

Рассчитаем корреляционный момент K_yz по формуле (2.5). Для этого определим M[YZ]:

M[YZ] = M[(3X₁ - X₂)(X₃ - 2X₁)] = M[3X₁X₃ - 6 -

- X₂X₃ + 2X₂X₁] = 3m₁m₃ - 6M[] -

- m₂m₃ + 2m₂m₁ = -6M[] - 12.

Так как D₁ = M[] - , то M[] = D₁ + = 8.

Таким образом, M[YZ] = -60. Тогда

K_yz = M[YZ] - m_y m_z = -60 - 9(-4) = -24.

Величину r_yz определим по формуле (2.6):

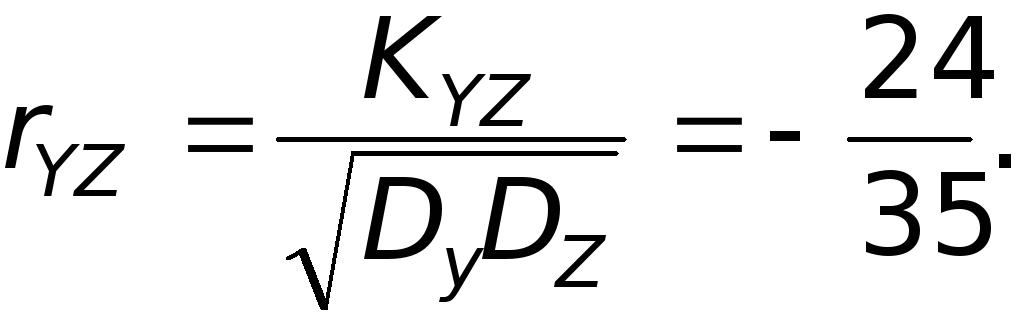
ЗАДАЧИ

4.1. Случайная величина X равномерно распределена от 0 до 1. Определить математическое ожидание и дисперсию величины Y =½X - 0,2½.

Ответ: m_y = 0,34, D_y = 0,0574.

4.2. Точка U, изображающая объект на круглом экране радиолокатора, распределена равномерно в пределах круга единичного радиуса. Найти дисперсию расстояния Y от точки U до центра экрана.

Ответ: D_y = 1/18.

4.3. Независимые случайные величины X и Y имеют нулевое математическое ожидание и единичную дисперсию. Найти коэффициент корреляции случайных величин U = 2X + Y и V = 2X - Y.

Ответ: r_uv = 0,6.

4.4. В треугольник с вершинами (0, 0), (0, 4), (4, 0) наудачу ставится точка (X, Y). Вычислить M[XY] и D[X + Y].

Ответ: M[XY] = 12/9, D[X + Y] = 8/9.

5. Оценка закона распределения

Генеральной совокупностьюназывается множество объектов, из которых производится выборка. Каждый из объектов задает фиксированное значение случайной величины.

Выборка - множество {x₁, x₂, ..., x_n} случайно отобранных объектов (значений) из генеральной совокупности.

Объемом выборки называется число ( n ) входящих в нее объектов.

Вариационным рядом называется выборка { } , полученная в результате расположения значений исходной выборки в порядке возрастания. Значенияназываются вариантами.