63.Двойственность кванторов. Открытые и замкнутые формулы.

ДО СТ ЕННОСТ - содержательное понятие, применяемое в логике и математике всякий раз, когда между двумя группами понятий установлено взаимно-однозначное соответствие так, что замена понятий одной группы на соответствующие понятия др. группы каждый раз переводит истинные высказывания в истинные высказывания. Понятие "Д." употребляется, напр., в логике (двойств. понятия: конъюнкция и дизъюнкция, квантор общности и квантор существования. См. Кванторы), в теории структур (двойственные понятия: "+" и "·"; 1 и 0), в теоретико-множественной

топологии (двойств. понятия: объединение и пересечение множеств).

Формула х называется замкнутой (или предложением), если множество (А) ее свободных переменных пусто (А(х) = ). Незамкнутые формулы называются

открытыми.

64. Формальная теория логики высказываний.

Логика высказываний (или пропозициональная логика) — это формальная теория, основным объектом которой служит понятие логического высказывания. С точки зрения выразительности, её можно охарактеризовать как классическую логику нулевого порядка. Логика высказываний является простейшей логикой, максимально близкой к человеческой логике неформальных рассуждений и известна ещё со времён античности. Также она является базой для более выразительных логик, таких как логика первого порядка а также логик высших порядков.

Базовыми понятиями логики высказываний являются пропозициональная переменная — переменная, значением которой может быть логическое высказывание, — и (пропозициональная) формула, определяемая индуктивно следующим образом:

1.Если P — пропозициональная переменная, то P — формула.

2.Если A — формула, то — формула.
3.Если A и B — формулы, то , и	— формулы.

4.Каждая формула может быть получена за конечное число шагов при помощи предыдущих трёх правил.

Знак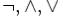и и (отрицание, конъюнкция, дизъюнкция и импликация) называются пропозициональными связками. Подформулой называется часть формулы, сама являющаяся формулой. Собственной подформулой называется подформула, не совпадающая со всей формулой.

Правила построения формул логики высказываний Элементарное высказывание (буква) является формулой нулевого уровня. Если

элементарное высказывание всегда верно, мы будем его обозначать буквой И, а если оно всегда неверно, — буквой Л. Тогда формулы первого уровня — это элементарные высказывания, к которым применена только одна логическая связка.

Пусть Ф1 и Ф2 — формулы ненулевого уровня. Тогда записи (¬(Ф1)), ((Ф1)&(Ф2)), ((Ф1)V(Ф2)), ((Ф1)->(Ф2)), ((Ф1)~(Ф2)) также являются формулами. Если же одна из формул Ф1 и Ф2 , к которым применяется логическая связка, имеет нулевой уровень, то она в скобки не заключается.

Истинностное значение Оценкой пропозициональных переменных называется функция из множества всех

пропозициональных переменных в множество {0, 1} (т.е. множество истинностных значений). Основной задачей логики высказываний является установление истинностного значения формулы, если дана оценка (т.е. определены истинностные значения входящих в неё переменных). Истинностное значение формулы в таком случае определяется индуктивно (с шагами, которые использовались при построении формулы) с использованием таблиц истинности связок.

65. Формальная теория логики предикатов.

ЛОГ КА ПРЕД КАТО — центральный раздел логики, в котором изучается субъектнопредикатная структура высказывании и истинностные взаимосвязи между ними.

Л.п. представляет собой содержательное расширение логики высказываний. В рамках данного раздела любое высказывание (пропозиция, предложение) рассматривается как некоторый структурно-сложный символ, разделяющийся на субъект, предикат и субъектно-предикатную связку. Субъект указывает на целостное понятие о предмете суждения; предикат — на к.-л. отдельное свойство, присущее предмету суждения; субъектно-предикатная связка — на отношение предикации (присущности), имеющее место между предметом суждения и отдельным свойством рассматриваемого предмета. Напр., в высказывании «Петр есть студент» слово «Петр» является субъектом, «студент» — предикатом, а слово «есть» — субъектно-предикатной связкой.

Так же, как и в логике высказываний, в Л.п. любое высказывание считается либо истинным, либо ложным. Однако при этом кроме пропозициональных связок «)», «&», «V», «—>», «<—>» используются еще три логических оператора: оператор предикации «<—», квантор общности «V» и квантор существования «Э». Если с помощью оператора предикации (субъектно-предикатной связки) формализуется внутреннее логическое строение высказываний об отдельных объектах, то с помощью кванторов формализуются высказывания о различных совокупностях объектов.

В естественном языке отдаленными смысловыми аналогами этих трех дополнительных операторов являются, соответственно, слова «есть (является)», «все» и «некоторые». Точный логический смысл этих операторов задается с помощью специальных семантических правил и формальных аксиом, постулируемых в соответствующем логическом исчислении. Наиболее распространено классическое исчисление предикатов, в котором из конечного числа аксиом по специальным правилам вывода могут быть получены общезначимые формулы Л.п., выражающие соответствующие логические законы. Средствами классического исчисления предикатов могут быть формализованы все основные типы высказываний силлогистики Аристотеля.

Для выявления субъектно-предикатной структуры высказываний вводится бесконечный перечень индивидных переменных: х, у, z, ..., х1, у1, zl, ..., представляющих различные объекты, и бесконечный перечень предикатных переменных: Р, Q, R, ..., Р1, Q1, Л1, ..., представляющих свойства и отношения объектов. Индивидные переменные принимают значения в произвольной (непустой) области; наряду с этими переменными могут вводиться индивидные константы, или имена собственные. Запись ("х)Р (х) означает «Всякий х обладает свойством Р»; ($х)Р(х) - «Некоторые х обладают свойством Р»; ($x)Q(xy) - «Существует х, находящийся в отношении Q с у» и т. п. Индивидная переменная, входящая в область действия квантора по этой переменной, называется связанной; переменная, не являющаяся связанной, называется свободной. Так, во всех трех приведенных формулах переменная х связана, в последней формуле переменная у свободна. Подлинной переменной является только свободная переменная: вместо нее можно подставить одно из ее значений и получить осмысленное выражение. Связанные переменные

называются фиктивными. Формула Л. п. называется общезначимой, если она истинна в каждой интерпретации. Тавтология логики высказываний является частным случаем общезначимой формулы. В Л. п., в отличие от логики высказываний, нет эффективного процесса, позволяющего для произвольно взятой формулы решить, является она общезначимой или нет.