ZO-2010

Ex = EIx + EIIx = k τa + k τa = k 2aτ , Ey = EIy = k τa .

Так как Ex и Ey взаимно перпендикулярны, то модуль результирующей напряженности находится по формуле

2τ ö2

τ ö2

τ

τ

æ

æ

5

Ex2 + Ey2 =

= k

Е =

4

+1

.

ç k

÷

+ ç k

÷

= k

a

a

è

a ø

è

a ø

Таким образом, искомая сила, действующая на точечный заряд со стороны заряженной нити, будет равна

F = Q1E = qτ 5 .

4πε0a

Проверим наименование единицы измерения силы в системе СИ

н.е.и. F = Кл × Кл × Н × м2 = Н . Кл2м × м

Подставим числовые значения и произведём вычисления

			1×10−71×10−6
	F =			5		= 4,02	×10−3	H.
			× 3,14 ×8,85×10−12 ×0,5
	4
Ответ: заряд Q	и заряженная нить взаимодействуют с силой F = 4,02 10–3 Н.
1

ЗАДАЧИ

201.В вакууме в вершинах правильного шестиугольника со стороной a =

=0,1 м расположены точечные заряды Q , 2Q , 3Q , 4Q , 5Q , 6Q (Q = 0,1 мкКл).

Найти силу F , действующую на заряд Q = Q0 , лежащий в плоскости шестиугольника и равноудаленный от его вершин.

202. Два точечных заряда Q1 > 0 и Q2 = −4Q1 закреплены на расстоянии r =

= 60 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q3 , так, чтобы он находился в равнове-

сии. Указать, какой знак должен иметь заряд Q3, чтобы равновесие было устойчивым.

203. В вершинах квадрата со стороной а = 0,1 м находятся одинаковые заряды Q1 = Q2 = Q3 = Q4 = = Q = 0,3 нКл каждый. Найти силу F1 , действующую на заряд

Q1 со стороны остальных трех зарядов, если система зарядов находится в парафине (диэлектрическая проницаемость ε = 2).

204. Тонкий стержень длиной l = 20 см находится в вакууме и несет равномерно распределенный заряд Q = 150 нКл. На продолжении оси стержня на рас-

стоянии a = 30 см от ближайшего его конца находится точечный заряд Q1 = =100

нКл. Определить силу F взаимодействия заряженного стержня и точечного заряда.

31

205. Тонкий полубесконечный стержень находится в вакууме и равномерно заряжен с линейной плотностью τ = 100 нКл/м. На перпендикуляре к оси стержня, восстановленном из конца стержня, находится точечный заряд Q = 50 нКл.

Расстоянии a заряда от конца стержня равно 30 см. Определить силу F взаимодействия заряженного стержня и точечного заряда.

206. Тонкая нить длиной l = 10 см находится в вакууме и равномерно заряжена с линейной плотностью τ = 10 нКл/м. На расстоянии a = 15 см от нити, против ее середины, находится точечный заряд Q = 1 нКл. Вычислить силу F , дейст-

вующую на этот заряд со стороны заряженной нити.

207. Тонкий стержень длиной l = 25 см несет равномерно распределенный заряд Q = 100 нКл. Определить напряженность E электростатического поля, созда-

ваемого в вакууме распределенным зарядом в точке, лежащей на перпендикуляре к стержню, проведенном через один из его концов, на расстоянии a = 10 см от этого конца.

208. Тонкая бесконечная нить несет заряд, равномерно распределенный с линейной плотностью τ = 1 мкКл/м. Определить модуль и направление силы F , действующей в вакууме на точечный заряд Q = 0,1 мкКл, расположенный на рас-

стояние a = 20 см от нити и удалённый от её конца на d = 40 см.

209. Тонкий диск радиусом R = 8 см несет равномерно распределенный заряд Q = 1 нКл. Определить напряженность E электростатического поля в вакууме в

точке A, лежащей на оси диска на расстоянии a = 6 см от его центра.

210. Тонкое кольцо радиусом R = 8 см несет равномерно распределенный с заряд Q = 15 нКл. Определить силу F , действующую в вакууме на точечный за-

ряд Q1 = 25 нКл, расположенный в точке A, равноудаленной от всех точек кольца на расстояние r = 10 см?

Тема 9. Поток вектора напряженности электростатического поля. Принцип суперпозиции. Теорема Гаусса и её применение для расчета напряженности электростатического поля в вакууме и веществе.

Пример решения задач

Бесконечно длинный цилиндр радиусом R1 = 5,00 см заряжен с объёмной плотностью ρ = 1,00 нКл/м3. Вокруг цилиндра, коаксиально с общей осью с ним, расположена цилиндрическая сетка радиусом R2 = 10,0 см. Сетка за-

ряжена с поверхностной плотностью σ = –2,00 нКл/м2. Вычислить напря- жённость электростатического поля E в точках, расположенных на рас- стояниях r1 = 2,00 см, r2 = 8,00 см, r3 = 15,0 см от оси цилиндра.

32

Дано

R1 = 5,00 см

ρ = 1,00 нКл/м3 R2 = 10,0 см

σ = – 2,00 нКл/м2 r1 = 2,00 см

r2 = 8,00 см r3 = 15,0 см E1, E2, E3 = ?

Анализ и решение

Электростатическое поле создано зарядами, равномерно распределенными по объёму цилиндра и по поверхности сетки. Эти тела являются симметричными относительно оси OO1, проходящей через их геометрические центры. Поэтому можно считать, что поле также обладает осевой симметрией, то есть его силовые линии являются прямыми в любой плоскости, перпендикулярной оси и направлены по радиусу. Такая симметрия позволяет искать напряженность поля с помощью теоремы Гаусса:

R1 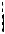O R2

E3			E1		E2
S3	S2	S1	r1	r2	h
r3

OI

Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленных на ε0 .

	r r	r	r	1	n
					åQi ,
	ФЕ = ò EdS	= ò EdS cos(E	dS) = ò EndS =
	S	S	S	ε0 i =1

= r

здесь dS dSn – вектор, модуль которого равен элементу поверхности dS , а его направление совпадает с направлением внешней нормали n к элементу поверхно-

сти, En – проекция вектора E на нормаль n к элементу поверхности dS .

В качестве произвольной замкнутой поверхности следует выбрать поверхность, коаксиальную заряженным поверхностям, то есть в виде соосного цилиндра конечной высоты. Характер зависимости E(r) для точек, лежащих внутри ци-

линдра, между цилиндром и сеткой и вне сетки, различен. Поэтому следует использовать три вспомогательные цилиндрические поверхности S1 , S2 , S3 с ра-

33

диусами r < R1, R1 < r2 < R2 и r3 > R2 (см. рисунок). Для каждой поверхности теорема Гаусса может быть записана в виде

			1	n
	ò	EndS =		åQi .	(1)
	S1,2,3		ε0 i=1

Из рисунка видно, что боковые поверхности вспомогательных цилиндров и их основания находятся в разных условиях относительно силовых линий поля. Во

всех точках основания (E ^ dS) = 90° и поток вектора напряженности сквозь основания равен нулю. На боковых поверхностях Sбок1,2,3 нормаль n совпадает с

направлением вектора E . Поэтому
ò EndS =	òEndS ,
S1,2,3	Sбок1,2,3

т.к. при такой форме произвольной замкнутой поверхности вычисление потока вектора напряженности электрического поля сводится к арифметическим действиям вместо интегрирования. Все точки боковых поверхностей находятся в одинаковых условиях относительно зарядов, что позволяет считать En постоянной

величиной. Тогда

ò	EndS = En ò dS = En 2π rh.	(2)
Sбок1,2,3	Sбок1,2,3

Здесь r и h – радиус и высота вспомогательных поверхностей. Следует обратить внимание, что r – это расстояния от оси цилиндра до точек, в которых вычисляется напряженность поля и одновременно радиусы произвольных поверхностей.

Сумма зарядов, охваченных вспомогательной поверхностью, стоящая в правой части выражения (1), зависит от радиуса произвольной поверхности.

При r < R1, внутри поверхности S1 , находится часть заряда цилиндра, а так как

заряд распределён равномерно, то Q1 = ρV1, где V1 = π r12h – объём, заключённый внутри поверхности S1 . Таким образом

n

Q1 = åQi = ρπ r12h .

i=1

Подставляя последнее выражение в (1) и заменяя интеграл по замкнутой поверхности S1 правой частью равенства (2), получаем

E	2π r h =	1	ρπ r2h , откуда E =		ρr1	.
n	1	ε0	1	n	2ε0
1				1

Проверим наименование единицы измерения напряженности в системе СИ

	н.е.и. Е =	Кл × м × Нм2	=	Н	.
		м3 × Кл		Кл

В полученную формулу подставим численные значения величин и произведём вычисления

34

E	=	1,00×10−9 × 2,00 ×10−2			=1,13 Н/Кл.
				2 ×8,85×10−12
n1
При R1 < r2 < R2 внутри				поверхности S2 , находится заряд Q2 = ρV2 , где

V2 = π R12h – объём цилиндра, заключённого внутри поверхности S2 . Тогда

n

åQi = Q2 = ρπ R12h .

i=1

Подставляя это выражение в (1) и заменяя интеграл по замкнутой поверхности S2 правой частью равенства (2), получаем

		1	2		ρR2
E	2π R h =		ρπ R	h , откуда E =	1	.
n	1	ε0	1	n	2r2ε0
2				2

Проверим наименование единицы измерения напряженности в системе СИ

	н.е.и. Е =	Кл × м × Нм2	=	Н	.
		м3 × м × Кл		Кл

Подставим числовые значения величин и произведём вычисления

	E	=	1,00 ×10−9 × (5,00 ×10−2)2		=1,77 Н/м.
			2 ×8,00×10−2	×8,85×10−12
	n2

При r3 > R2 внутри поверхности S3 поле будет создаваться заряженными цилиндром и сеткой. Тогда

n

åQi = Q3 = (ρπ R12h +σ 2π R2h) .

i=1

Здесь 2π R2h – площадь поверхности сетки, по которой равномерно распределён

заряд с поверхностной плотностью σ . Подставляя значение заряда в (1) и заменяя интеграл по замкнутой поверхности S3 правой частью равенства (2), получаем

E

× 2π r h =

1

(ρπ R2h + 2σπ R h), откуда E =

1

(ρR2

+ 2σ R ).

n

3

1

2

n

2r3ε0

1

2

3

ε0

3

Проверим наименование напряженности в системе СИ

наимен.Е =

Н × м2

Кл × м2

Кл × м

Н

(

3

+

2

) =

.

м × Кл

2

м

Кл

м

Подставим числовые значения величин и произведём вычисления

E

=

1

é1,00 ×10−9

(5,00×10−2 )2 - 2 × 2,00×10−9 × 0,1ù

= -149,8 Н/м.

n3

2 × 0,15×8,85×10−12 ë

û

Знак « – » означает, что угол между векторами E3 и dS равен 180° (см. рис.). Ответ: напряжённости поля в трёх точках соответственно равны E1 =1,13 Н/м,

E2 =1,77 Н/м, E3 =149,8 Н/м.

35

ЗАДАЧИ

211. Металлическая сфера радиусом R = 10 см, находящаяся в вакууме, несет равномерно распределенный заряд Q = 1 нКл. Определить напряженность E

электрического поля в следующих точках: 1) на расстоянии r1 = 8 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии r3 = 15 см от центра сферы. Построить график зависимости E = E(r) .

212.Две концентрические металлические заряженные сферы радиусами R1 =

=6 см и R2 = 10 см находятся в вакууме и несут соответственно заряды Q1 =

=1 нКл и Q2 = –0,5 нКл. Найти напряженность E поля в точках, отстоящих от центра сфер на расстояниях r1 = 5 см; r2 = 9 см; r3 = 15 см. Построить график зависимости E = E(r) .

213.Расстояние d между двумя длинными тонкими проволоками, расположенными параллельно друг другу, равно 16 см. Проволоки равномерно заряжены разноименными зарядами с линейной плотностью |τ | = 1,5 мкКл/м. Найти с по-

мощью теоремы Гаусса напряженность E поля в вакууме в точке A , удаленной на расстояние a = 10 см как от первой, так и от второй проволоки.

214.Две длинные тонкостенные соосные трубки радиусами R1 = 2 см и R2 =

=4 см находятся в вакууме и несут заряды, равномерно распределенные по длине

слинейными плотностями τ1 = –1 нКл/м и τ2 = 0,5 нКл/м.. Определить напря-

женность Е поля в точках, находящихся на оси трубок на расстояниях r1 = = 1 см; r2 = 3 см; r3 = 6 см. Построить график зависимости E = E(r) .

215. Эбонитовый (диэлектрическая проницаемость ε = 3) сплошной шар радиусом R = 5 см несет заряд, равномерно распределенный с объемной плотностью ρ = 10 нКл/м3. Определить напряженность E электрического поля в точках: 1) на расстоянии r1 = 3 см от центра шара; 2) на поверхности шара; 3) на расстоянии r3 = 10 см от центра шара. Построить график зависимости E = E(r) .

216. Полый стеклянный шар (диэлектрическая проницаемость ε = 7) несет равномерно распределенный по объему заряд. Его объемная плотность ρ = = 100 нКл/м3. Внутренний радиус R1 шара равен 5 см, наружный – R2 = 10 см.

Вычислить напряженность E электрического поля в точках, отстоящих от центра сферы на расстоянии: 1) r1 = 3 см; 2) r2 = 6 см; 3) r3 = 12 см. Построить график

зависимости E = E(r).

217. Очень длинный парафиновый (диэлектрическая проницаемость ε = 2) цилиндр радиусом R = 2 см несет заряд, равномерно распределенный по объему с объемной плотностью ρ = 10 нКл/м3. Определить напряженность E электрического поля в точках, находящихся от оси цилиндра на расстоянии: 1) r1 = 1 см; 2) r2 =

= 3 см. Построить график зависимости E = E(r) .

36

218. Электрическое поле создано в вакууме двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями σ1 = 2 нКл/м2 и σ2 = –5 нКл/м2. Определить напря-

женность E поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.

219. Две круглые параллельные пластины радиусом R = 10 см находятся в вакууме на малом (по сравнению с радиусом) расстоянии друг от друга. Пластинам сообщили одинаковые по абсолютному значению, но противоположные по знаку заряды Q1 = Q, Q2 = −Q, Q > 0. Определить этот заряд Q , если пластины притяги-

ваются с силой F = 2 мН. Считать, что заряды распределены по пластинам равномерно.

220. Равномерно заряженная плоскость, расположена в вакууме в поле тяжести Земли перпендикулярно вектору g , имеет поверхностную плотность электриче-

ских зарядов σ = 12 мкКл/м2. Над ней находится однородный железный шарик, имеющий заряд Q = 3 мкКл. Какой радиус R должен иметь шарик, чтобы он не

падал? Расчет напряженности электростатического поля провести с помощью теоремы Гаусса для бесконечной плоскости.

Тема 10. Потенциал и потенциальная энергия электростатического поля, созданного точечными зарядами, зарядами распределенными по линии, кольцу и плоскости. Принцип суперпозиции электростатических полей.

Пример решения задач

По тонкой проволочной нити, изогнутой по дуге окружности радиусом R , равномерно распределён заряд с линейной плотностью τ = 10,0 нКл/м. Опре- делить потенциал электрического поля ϕ , создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги. Длина нити l составляет 1/3 длины окружности.

Дано

τ = 10,0 нКл/м l = 13 (2π R)

ϕ = ?

Анализ и решение

Электростатическое поле создано зарядом, распределенным по тонкой дуге. Оно не обладает достаточной симметрией, и указать точную конфигурацию силовых линий электростатического поля невозможно. Поэтому для нахождения энергетической характеристики поля – потенциалаϕ , можно использовать только

37

принцип суперпозиции. Разобьем дугу на элементарные участки длиной dl . Заряд dQ , находящийся на этом участке, можно считать точечным. Тогда потенциал

dϕ , создаваемый в центре кривизны таким зарядом, рассчитаем по формуле

			dϕ = k	dQ	,	(1)
		1		r
	где k =		, r – расстояние от элемента dl		до точки, потенциал в которой мы
		4πε0

вычисляем. Потенциал результирующего поля получим интегрированием выражения (1)

		ϕ = ò dQk ,		(2)
		Q	r
где интеграл берется по всему заряду Q , создающему поле.
Равномерное распределение заряда по дуге позволяет утверждать, что
dQ	= Q	, откуда dQ = Q dl =τ dl .
dl	l		l

Здесь τ – линейная плотность заряда дуги. Тогда формула (2) примет вид

ϕ = kòτ dl .

l r

Произведём интегрирование, учитывая, что r = R , а длина нити меняется от 0 до

l = 1

2π R

3

2

π R

τ dl

τ

2

π R = k

τ 2π R .

ϕ = 3

ò

k

= k

l

03

R

R

R 3

0

Заменим k её значением, произведем сокращение и получим окончательную формулу

ϕ = 6τε0 .

Проверим наименование единицы измерения потенциала в системе СИ

н.е.и. ϕ =	Кл ×Y × м2	=	Дж	= В .
	м × Кл2		Кл

Подставим числовые значения величин и произведём вычисления

ϕ =		10,0 ×10−9	=188,3 В.
		×8,85×10−12
6

Ответ: создаваемый заряженной дугой в её центре потенциал ϕ = 188,3 В.

38

ЗАДАЧИ

221.Найти потенциальную энергию Eп системы трех точечных зарядов Q1 =

=10 нКл, Q2 = 20 нКл и Q3 = –30 нКл, расположенных в вакууме в вершинах равностороннего треугольника со стороной a = 10 см.

222.Определить потенциальную энергию Eп системы четырех точечных заря-

дов, расположенных в вакууме в вершинах квадрата со стороной a = 10 см. Заряды одинаковы по абсолютной величине | Qi | = 10 нКл (i = 1 ÷ 4), но два из них отрицательны, причем заряды одного знака расположены по диагоналям квадрата.

223. Тонкие стержни в вакууме образуют квадрат со стороной a . Стержни заряжены с линейной плотностью τ = 1,33 нКл/м. Найти потенциал ϕ в центре квадрата.

224. По тонкому кольцу радиусом R = 10 см, расположенному в вакууме, равномерно распределен заряд Q = 5 нКл. Определить потенциал ϕ в точке A, ле-

жащей на оси кольца, на расстоянии a = 5 см от центра.

225. Бесконечно длинная тонкая прямая нить, расположенная в вакууме, несет равномерно распределенный по длине нити заряд с линейной плотностью τ =

= 0,01 мкКл/м. Определить разность потенциалов ϕ	двух точек поля, удален-
12

ных от нити на расстояния r1 = 2 см и r2 = 20 см.

226. Тонкий стержень длиной l = 10 см, расположенный в вакууме, несет равномерно распределенный заряд Q = 1,5 нКл. Определить потенциал ϕ электриче-

ского поля в точке A, лежащей на оси стержня на расстоянии a = 20 см от ближайшего его конца.

227. Тонкая круглая пластина радиусом R = 10 см находится в вакууме. Она равномерно заряжена с поверхностной плотностью заряда σ = 1 нКл/м2. Определить потенциал ϕ электрического поля в двух точках: 1) в точке 1, расположенной в центре пластины; 2) в точке 2, лежащей на оси, перпендикулярной плоскости пластины и отстоящей от центра пластины на a = 5 см.

228. В вакууме расположены две концентрические металлические сферы радиусами R1 = 3 см и R2 = 6 см. Заряд внутренней сферы Q1 = –1 нКл, внешней –Q2 = 2

нКл. Найти потенциал ϕi электрического поля на расстоянии: 1) r1 = 1 см; 2) r2 = 5 см; 3) r3 = 9 см от центра сфер. Построить график зависимости ϕ = ϕ(r).

229. Сплошной парафиновый шар (ε = 2) радиусом R = 10 см находится в вакууме и равномерно заряжен с объемной плотностью p = 1 мкКл/м3. Определить

потенциал ϕ электрического поля в центре шара и на его поверхности. Построить график зависимости ϕ = ϕ(r).

230. Эбонитовый (ε = 3) толстостенный полый шар находится в вакууме и несет равномерно распределенный по объему заряд с плотностью p = 2 мкКл/м3 . Внут-

39

ренний радиус шара R1 = 3 см, наружный R2 = 6 см. Определить потенциал ϕ ша-

ра в следующих точках: 1) на наружной поверхности шара; 2) на внутренней поверхности шара; 3) в центре шара. Построить график зависимости ϕ = ϕ(r)

Тема 11. Работа по перемещению зарядов в электростатическом поле. Движение заряженных частиц в электростатическом поле.

Пример решения задач

Точечный заряд Q2 = – 1,00 мкКл расположен на продолжении диаметра

заряженного шара. Какую работу надо совершить, чтобы перенести этот заряд из точки 1 в точку 2 поля, созданного шаром. Потенциал шара

ϕшара = 1,00 кВ?

Дано

Q2 = – 1,00 мкКл ϕшара = 1,00 кВ

A* = ?

Анализ и решение

Работа A *, совершаемая внешними силами при перемещении заряда Q в ку-

лоновском поле, равна работе сил поля, взятой с обратным знаком:
A* = −A12 = −Q(ϕ1 −ϕ2) ,	(1)

здесь ϕ1 и ϕ2 – потенциалы соответственно начальной и конечной точек. Для то-

го чтобы определить знак работы внешних сил, надо выяснить направление силовых линий поля. Как видно из рисунка, при движении заряда Q2 из точки 1 по на-

правлению к точке 2 заряд перемещается по силовой линии, то есть против кулоновских сил, и работа внешних сил будет положительна.

Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала E = −gradϕ . Для поля с осевой

симметрией, каким является поле шара, это соотношение можно записать в виде

E = −dϕ / dr или dϕ = −Edr .

Интегрируя последнее выражение, найдем разность потенциалов двух точек, отстоящих на r1 и r2 от центра шара

r2
(ϕ1 − ϕ2 ) = ò Edr .	(2)

r1

Используя теорему Гаусса, можно показать (см. пример из Темы 9), что равномерно заряженный шар радиуса R и зарядом Q1, создает электростатическое по-

ле:

40