mgl
	ω02 =					I			mgl
			→ ω0	=				T = 2π	I		– для физического маятника называют-
		I				mgl

ся циклическими (круговыми) частотами (в скобках периодами) колебаний. Тогда динамическое уравнение колебаний пружинного маятника имеет вид

d 2 x + ω2 x = xΙΙ + ω2 x = x + ω2 x = 0.
dt2			0			0			0
Динамическое уравнение колебаний физического маятника
d 2ϕ	+	mgl	ϕ = ϕ	ΙΙ	+	mgl	ϕ = ϕ+		mgl	ϕ = 0 .
dt2		I				I			I
Решением этого уравнения				являются				функции ϕ = ϕ0 sin(α)ω0t +			или

ϕ = ϕ0 cos(α)ω0t + .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

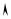FAp2

FAp1

•	•
h	h
mg	mg

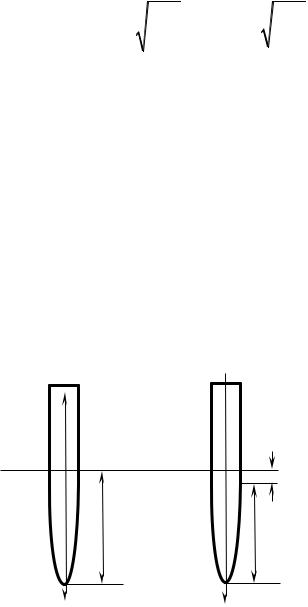
Задача 1. Ареометр, покоящийся в жидкости плотностью ρ , подтолкнули

вниз и он начал совершать колебания. Найти период малых колебаний ареометра, если его масса m , а площадь попе-

x речного сечения трубки S .

Решение. В состоянии покоя часть ареометра погружена на глубину h . На него будут действовать сила тяжести и сила Архимеда, равная силе тяжести, вытесненной ареометром жидкости:

FАp = mжидкg = ρShg

FАp = mжидкg = ρShg

где ρ – плотность жидкости; Sh =V − объем вытесненной ареометром жидкости.

Динамическое уравнение для этого состояния имеет вид
0 = mg + FАp.	(1)

Когда ареометр толкнули вниз, он погрузился на глубину h + x и динамическое уравнение для этого состояния запишется в виде

ma = mg + FÀp2 , где FÀp2 = ρSg(h + x) .	(2)
В проекциях на оси координат уравнения (1) и (2) запишутся как
OX 0 = mg −ρShg → mg = ρShg ,	(3)

50

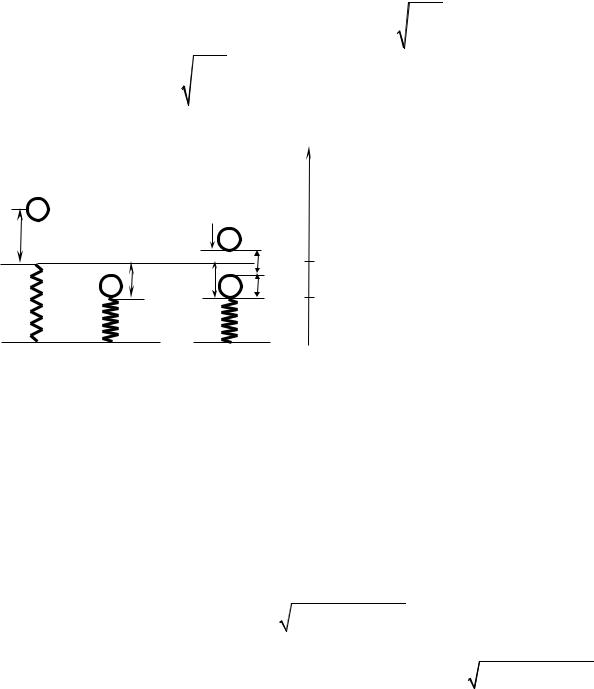
	OX ma = m	d 2x	= mg −ρSg(h + x) .	(4)
		dt2

Подставим в уравнение (4) уравнение (3) и, проведя преобразования, получим формулу

m

d 2x

= −ρgSx

→ m

d 2x

+ρgSx = 0 .

(5)

dt2

dt2

Уравнение (5) является дифференциальным уравнением колебаний арео-

метра в жидкости. Отсюда имеем

d 2x

+

ρgS

x = 0

. Это динамическое уравнение

dt2

m

гармонических

колебаний, где

2

ρgS

→ ω =

ρgS

и период

колебаний

ω =

0

m

0

m

ареометра равен

T = 2π

m

.

ρgS

h		x2	x0
	x
		x1	x0
I	II

y	Задача 2. Пружина с коэффи-
	циентом жесткости k стоит на сто-
	ле. С высоты h , где h отсчитыва-
	ется от верхнего положения пру-
	жины до точки равновесия колеб-
0	лющегося шарика, на пружину па-
	дает шарик массой m и прилипает
x	к пружине (абсолютно неупругий
	удар). Найти амплитуду колебаний
	шарика (h отсчитывается от верх-
	него края пружины).

Решение. В момент соприкосновения шарика с пружиной образуется система шарик–пружина, где телом, совершающим колебания, является шарик. В начальный момент шарик обладает потенциальной энергий Eнач = mgh. Конеч-

ная энергия состоит из потенциальной энергии покоящегося шарика, в нижнем

его положении и энергии пружины E

=

kx2

− mgx , где x – максимальная де-

кон

2

формация пружины, при которой скорость шарика равна нулю

E = E →

kx2

− mgx = mgh

→

kx2

− mgx − mgh = 0,

кон

нач

2

2

x =

mg ±

(mg)2

+ 2kmgh

.

k

Шарик будет

совершать колебания

от

x

=

mg +

(mg)2

+ 2kmgh

до

1

k

51

mg −

(mg)2

+ 2kmgh

x + x

x

=

. Амплитуда колебаний шарика равна x

=

1 2

,

2

k

ì àêñ

2

x

=

(mg)2

+

2kmgh

.

макс

k

Шарик будет колебаться с амплитудой x около положения равновесия.

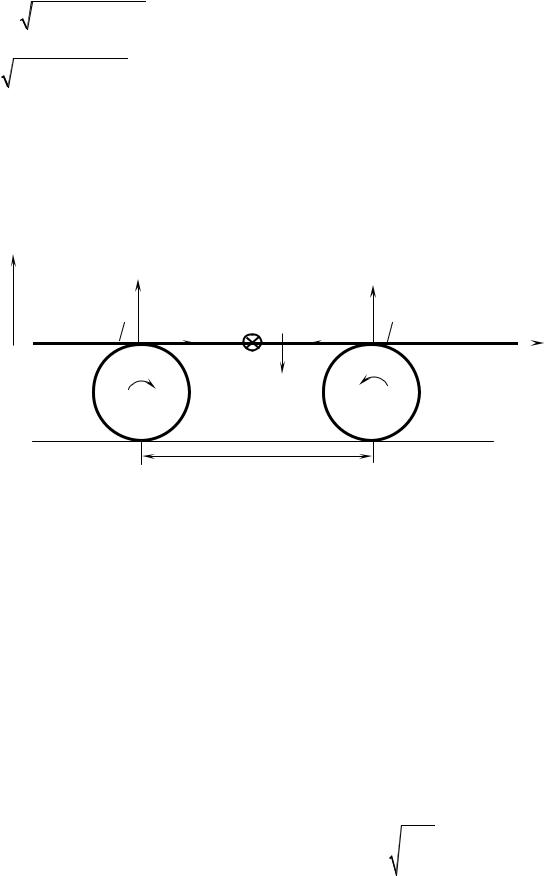
Задача 3. На два одинаковых диска 1 и 2 , расположенных на расстоянииl и вращающихся с одинаковыми угловыми скоростями навстречу друг друга, кладут длинный стержень. Коэффициент трения между дисками и стержнемµ. Найти пе-

риод малых колебаний стержня.

y
N1	N2

− 2		•C			2
	Fтр1 z 0 xC Fтр2						x
		mg		•
	•ω			ω

Решение. Анализ условия задачи показывает, что на стержень действуют

силы: mg, N , N	, F	, F . Динамическое уравнение имеет вид
1 тр12	тр2

ma = mg + N + N				+ F + F
		1 тр1 2		тр2
и проекция его на ось OX m	d 2x	= F	− F		= µ(N	− N	2	) . В этом уравнении
	dt2	тр1		тр2	1

неизвестна разность (N1 − N2 ). Найдем эту разность, записав уравнение ди-

намики вращательного движения относительно оси, проходящей через середину стержня и перпендикулярной стержню, относительно которой происходят колебания стержня.

Тогда

Iβ = N

l

+ mgx − N

l

.

Стержень

не

совершает

вращательного

2 2

1 2

движения

вокруг

этой

оси,

т.

е.

β = 0

и

0 = N

l

+ mgx − N

2

l

→ N − N

2

= − 2mgx .

1

1

Дифференциальное уравнение колебаний стержня принимает вид

2

2

l

d 2x

2µmg

x → ω2 =

2µg

l

m dt2 = −

l

→T

= 2π

.

l

2µg

52

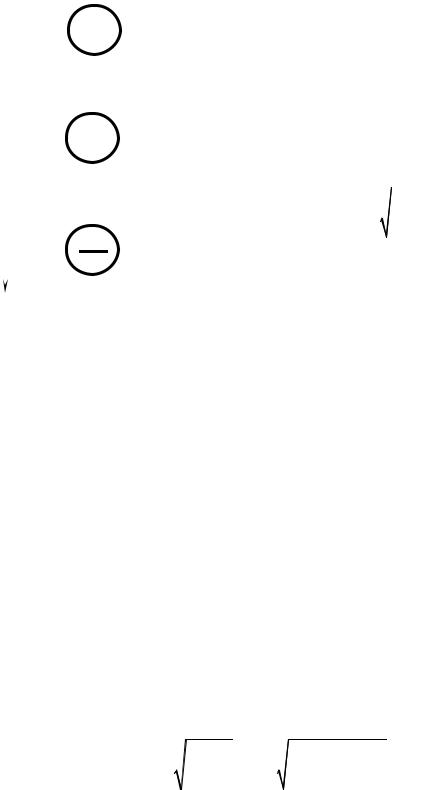
Задача 4. Физический маятник представ-

ляет собой стержень массой M , длиной l , на

котором расположены три груза одинаковой

массы m . Грузы расположены от оси подвеса

на расстояниях 1 l,

2 l и l . Определить период

•

m1

3

3

3

колебаний стержня относительно оси подвеса.

Решение. Физический маятник представ-

ляет собой систему, состоящую из четырех тел:

2

•

m2

стержень и три груза, подвешенных в различ-

3

ных местах стержня. Период колебаний такой

системы запишется в виде

T = 2π

I

,

m gr

•

m3

c

0

где I − момент инерции физического маятника,

y

представляющий собой сумму моментов инер-

ции тел, входящих в систему.

I = Iстерж + Iгр1 + Iгр2 + Iгр3.

Момент инерции стержня равен Iстерж = 13 Ml2 и моменты инерции грузов как материальных точек равны

		l			2			2	2
	Iгр1	=				, Iгр2	= m		l	, Iгр3 = ml2 .
			3					3

Момент инерции физического маятника равен

I = Iст + Im

+ Im

+ Im .

+ ml2

1

2

3

I =

1 Ml2

+ 1 ml2

+

4 ml2 + ml2 → I =

1 Ml2

(1+ 2 +3) =

1 Ml2

+ 2ml2 =

3

9

9

3

3

3

= l

2

1

M

2 3M +14m

.

3

+ 2m → I = l

9

Центр масс маятника находится по формуле

l

1

2

r =

M

+ 3 ml +

3 ml + ml

= l(3M +1 m2) =

l(M + 4m)

.

2

0

M + m + m + m

6(M −3m) 2(M +3m)

Масса всей системы равна mc = M + m + m + m = M +3m .

Период колебаний физического маятника будет равен

T = 2π

I

=

2π l(3M +14m) .

m gr

3

g(M + 4m)

0

c

53