ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Пусть функция f (x) задана на отрезке [a, b]. Разобьем этот отрезок на n отрезков [xk −1, xk ], причем a = x0 < x1 < ... < xn = b. Сопоставим это разбиение с

n	, ξk [xk −1, xk ]. Потре-
интегральной суммой ∑ f (ξk )∆xk , где ∆xk = xk − xk −1
k −1

буем, чтобы max[xk −1, xk ]→ 0 при числе разбиений n → ∞. Соответствующий предел интегральной суммы называется определенным интегралом и обознача-

b		n
ется ∫ f (x)dxξ= )lim ∑ f ( k ∆xk . Если F(x) первообразная функции f (x) , то
a		n→∞ k =1	b
справедлива формула Ньютона–Лейбница ∫ f (x)dx = F(x)Ιba = F(b) − F(a) .
			a
		СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
	b	b
1. ∫Af (x)dx = A∫ f (x)dx			(A = const).
	a	a
	b	b	b
2. ∫( f (x) ± g(x))dx = ∫ f (x)dx ± ∫g(x)dx .
	a	a	a
	a	a
3.	∫	f (x)dx = 2∫ f (x)dx , если функция f (x) четна на отрезке (−a; a).
	−a	0
	a
4.	∫	f (x)dx = 0, если функция f (x) нечетна на (−a; a).
	−a
	b	b
5. ∫ fdϕ = f ϕ Ιba − ∫ϕdf , где f = f (x) и ϕ = ϕ(x) непрерывны и имеют свои
	a	a

производные. Формула (5) называется формулой интегрирования по частям.

КИНЕМАТИКА

Твердое тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой (частицей). Если размеры тела велики, то тело разбивают на систему материальных точек, к каждой из которых применяют физические законы и после этого производят суммирование для получения конечного результата. Положение материальной точки или твердого тела в пространстве можно определить только по отношению к другому, произ-

6

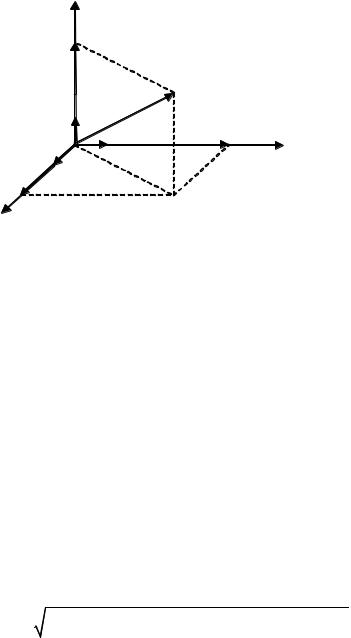
вольно выбранному телу, называемого телом отсчета. Выбранное таким образом тело условно считается неподвижным и относительно него рассматривается положение или движение исследуемой материальной точки или твердого тела. Тело отсчета и часы образуют систему отсчета. Для количественного описания движения материальной точки с системой отсчета жестко связывают систему координат. Наиболее часто используют декартову (прямоугольную), полярную, сферическую и цилиндрическую системы координат.

У

Уj

	j	i	r	Xi	X
	k

Z

Положение материальной точки в пространстве, в декартовой системе ко-

ординат, определяется радиусом-вектором r =УXij +Zk +

(см. рис.), прове-

денным из точки наблюдения в точку нахождения исследуемой материальной точки, где i , j, k – единичные векторы на соответствующие оси координат Õ, Ó, Z . Если материальная точка находится в точке А пространства то

rХ=i	У +j	Z +k	A	, где r	– вектор, начинающийся в начале координат и
A	A	A		A	XA , УA, ZA – проекции вектора rA на оси коор-
заканчивающийся в точке А.

динат X , Ó, Z. Перемещение материальной точки из точки А в точку В характеризуется вектором перемещения ∆r = rB − rA . В проекции на оси декартовой системы координат он равен

∆rХ= Х− r, ∆ У= У− r, ∆ Z= Z−

A

.

x

B

A

y

B

A

z

B

Модуль вектора перемещения равен

∆r

= У(X У− X

A

)2 Z+ ( Z−

A

)2

+ (

B

−

A

)2

.

B

B

Вектор скорости (мгновенной скорости), характеризует быстроту и направление движения частицы в каждый момент времени. Он определяется как первая производная от радиуса-вектора r по времени

V = drdt = dXdt i + dÓdt j + dZdt k .

7

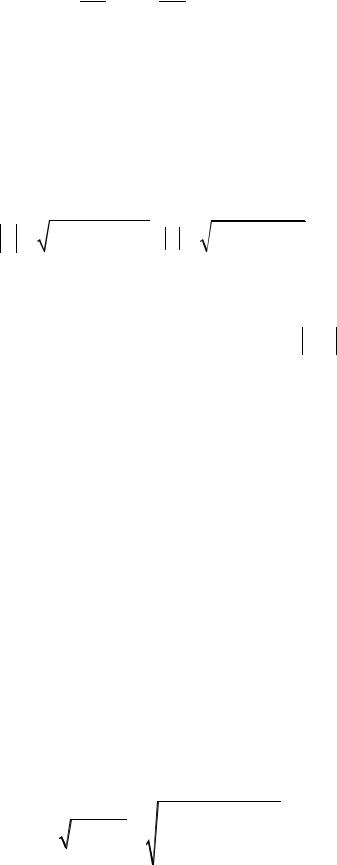
Следовательно, проекции вектора скорости на соответствующие оси декартовой системы координат равны

Vx = ddtХ , Vy = ddtУ , Vz = dZdt .

Вектор ускорения материальной точки, показывающий быстроту изменения направление и модуля вектора скорости, равен

a =

d 2r

dVУ d 2 Xd

Z d 2

2

dVdV

dV

y

z

=

=

i

+

j +

k

=

x

i +

j +

k .

dt2

dt

dt2

dt2

dt

2

dt

dt

dt

Проекции вектора ускорения на координатные оси равны

dХ

dV

dУ

dVy

d

2

Z

dV

ax =

2

=

x ,

ay =

2

=

, az =

=

z .

dt2

dt2

dt

dt

2

dt

dt

Модули векторов скорости и ускорения равны

V = 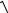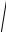Vx2 +Vy2 +Vz2 , a = 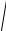ax2 + a2y + az2 .

Вектор скорости направлен по касательной к траектории. Его можно представить в виде V =V τ, где τ − единичный вектор, касательный к траектории и направлен в ту же сторону, что и вектор V .

Зная зависимость модуля скорости V от времени t (V (t) ) , можно вычислить путь, пройденный частицей за промежуток времени отt1 до t2 , по формуле

t2

S = ∫V (t)dt ,

t1

где V − модуль вектора скорости.

В случае криволинейного движения частицы по плоскости (криволинейная траектория) ускорение частицы представимо как сумма тангенциального ( aτ ) и нормального (an ) ускорений: a = aτ + an .

Тангенциальное ускорение aτ = dVdt τ характеризует быстроту изменения модуля скорости. Оно направлено по касательной к траектории. Модуль тан-

генциального ускорения равен		a			= dV .
		τ				dt
					V 2
Нормальное ускорение an =					R	n характеризует быстроту изменения на-
правления скорости (R − радиус кривизны траектории в месте нахождения ма-

териальной точки). Единичный вектор n τ и направлен в сторону вогнутости

траектории. Модуль

=

V 2

, Модуль вектора ускорения равен

an

R

dV 2

V 2

2

2

2

=

a

= aτ

+ an

+

.

dt

R

8

Углу поворота ∆ϕ тела, совершающего вращательное движение, можно поставить в соответствие вектор ∆ϕ, по мо дулю равный ∆ϕ и направленный вдоль оси вращения тела таким образом, чтобы из конца вектора ∆ϕ вращение тела происходило против часовой стрелки. Тогда вектор угловой скорости

ω= ddtϕ , а углового ускорения β = ddtω.

Связь между линейным и угловым скоростями осуществляется посредством формулы V =[ωr ], где r − радиус-вектор, проведенный из произвольной

точки, лежащей на оси вращения, в место нахождения материальной точки. Линейные ускорения связаны с угловым ускорением и угловой скоростью формулами an = ω2R , aτ =βR .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Вектор скорости материальной точки задается уравнением V = Ati − Bt3 j +Ñt5k . Найти: радиус-вектор, модуль радиуса-вектора, модуль

вектора скорости, ускорение и модуль ускорения материальной точки, если в момент времени t = 0, X = 0, Ó = 0, Z = 0.

Решение. Для решения этой задачи необходимо ознакомиться с физическими понятиями: радиус-вектор, проекции радиуса-вектора на оси декартовой системы координат, модуль радиуса-вектора, вектор скорости и модуль вектора скорости в декартовой системе координат, выражение вектора скорости через производную по времени от радиуса-вектора, проекции вектора скорости на оси декартовой системы координат через производные по времени от проекций ра- диуса-вектора на соответствующие оси координат, вектор ускорения и выражение его через производные по времени от радиуса-вектора и вектора скорости и выражение ускорения через проекции на оси координат, модуль вектора ускорения.

Анализ формулы для скорости из условия задачи показывает, что проекции вектора скорости на оси декартовой системы координат равны

Vx = At, Vy = Bt3, Vz = Ct5 . В общем случае вектор скорости определяется как

первая производная радиуса-вектора по времени:

V = drdt = dXdt i + dÓdt j + dZdt k =Vxi +Vy j +Vzk ,

где i , j, k – единичные векторы, задающие оси координат (X , Ó, Z) .

Следовательно, можно записать

dÕdt =Vx = At, dÓdt =Vy = Bt3, dZdt =Vz = Ct5,

dÕ =Vxdt = Atdt, dÓ =Vydt = Bt3dt, dZ =Vzdt = Ct5dt . Таким образом, пришли

к дифференциальным уравнениям, в которых переменные разделены. Решение получим, интегрируя левые и правые части уравнений с использованием на-

9

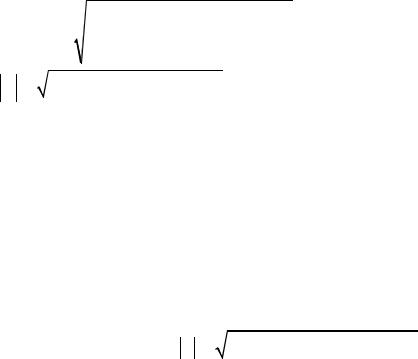
чальных данных:
	x			t						At2				t			At2					A02			At	2
	∫d Õ = ∫Atdt → x =												0		=						−		→ x =				,
										2								2				2			2
0				0
	y			t	3	dt → y =				Bt4				t	=		Bt		4		−	B04	→ y =		Bt		4
	∫dÓ = ∫Bt									4				0				4				4			4		,
0				0
	z			t	5		dt → z =			Ct6				t	=		Ct		6		−	C06	→ z =		Ct	6
	∫dZ = ∫Ct									6				0				6				6			6		.
0				0
																		2				Bt4		Ct6
															At
Радиус-вектор запишется в виде r												=				2		i		+		4	j +	6	k . Модуль радиуса-
вектора равен		=		At2	2				Bt4	2				Ct6 2								Модуль вектора скорости есть
	r			2				+	4	+					6			.

величина V = 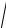(At)2 +(Bt3 )2 +(Ct5 )2 . Вектор ускорения запишем как вторую

производную по времени от радиуса-вектора или первую производную от вектора скорости, а его модуль – через вторую производную от проекций радиусавектора или через первую производную от проекций вектора скорости на оси координат

a

d 2r

d 2 X

d 2Ó

d 2Z

d 2

(At2 / 2)

= dt2 =

dt2

i

+

dt2

j

+ dt2

k

=

dt2

dV

dV

dVy

dV

d(At)

a =

=

x i

+

j +

z k

=

dt

dt

dt

dt

dt

= Ai +3Bt2

j +5Ct4k.

		d 2	(Bt4	/ 4)			d 2	(Ct6	/ 6)
i	+				j	+				k ,
			dt2					dt2
	+	d(Bt3 )			d(Ct5 )
i		dt		j +		dt		k =

Модуль вектора ускорения a = 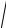(A)2 +(3Bt2 )2 +(5Ct4 )2 .

Задача 2. Уравнение движения частицы по окружности радиусом R задано через угол ϕ как функция времени ϕ = Bt3 . Найти: вектор угла ϕ, вектор уг-

ловой скорости, модуль вектора угловой скорости, углового ускорения, модуль вектора углового ускорения, вектор линейной скорости, модуль вектора линейной скорости, векторы тангенциального и нормального ускорений частицы, модули векторов тангенциального и нормального ускорений частицы, вектор полного линейного ускорения частицы, модуль полного линейного ускорения.

Решение. Для решения этой задачи необходимо ознакомиться с физическими понятиями: криволинейное движение частицы (частный случай криволинейного движения – движение по окружности), угол поворота и вектор угла поворота, вектор угловой скорости и его модуль, угловое ускорение и модуль вектора углового ускорения, вектор линейной скорости и модуль вектора линейной скорости, векторы тангенциального и нормального линейных ускоре-

10

ний частицы, вектор полного линейного ускорения и модуль полного линейного ускорения частицы.

В условии задачи задан угол ϕ в скалярном виде как функция времени. Модуль угловой скорости ω найдем как первую производную по времени от

угла ϕ, ω= ddtϕ . Векторы угловой скорости и угла поворота совпадают по на-

правлению и направлены по оси вращения частицы таким образом, чтобы из конца этих векторов вращение частицы происходило против часовой стрелки. Если в качестве оси вращения выбрать ось Z , то в векторном виде угловая ско-

рость запишется формулой ω= ddtϕ , а модули векторов ϕ и ω выразятся через

проекции этих векторов на ось Z → ωz = ddtϕz . Вектор углового ускорения находится, как первая производная от вектора угловой скорости или вторая производ-

d

2

dω

d

2

ϕ

ная от угла ϕ:

dω

=

ϕ

, а проекция на ось Z → βz =

z =

z

. Записав

β =

dt

dt

2

dt

dt2

d(Bt3)

ω=

dϕ

=

и выполнив дифференцирование, найдем угловую скорость

dt

dt

ω= 3Bt2 . Угловая скорость записана в скалярном виде. Чтобы записать ее в векторном виде, мы должны задать единичный вектор (например k ), направ-

ленный вдоль оси Z . Тогда вектор

dϕ

d(Bt

3

)

2

dϕ

=

=

= 3 Bt

ω=

dt

dt

z k

dt

k

k .

(3Bt2 )k = 6 Btk . Модуль вектора

Вектор углового ускорения равен β = dω

=

d

dt

dt

углового ускорения β = 6Bt . Вектор линейного ускорения a может быть записан через его проекции на ось τ, совпадающую по направлению с вектором ли-

нейной скорости V и перпендикулярную ей ось n и единичные векторы τ и n направленные вдоль этих осей a = aττ + ann . Проекции aτ и an связаны с ли-

	нейной скоростью соотношениями a	τ	=	dV	, a	n	=	V 2	. Тогда для вектора линей-
				dt				R
										V 2
									dV
	ного ускорения мы можем записать a = aτ τ + ann =								dt τ +	R n . Вектор линей-
											]. По модулю он
	ной скорости связан с угловой скоростью формулой V =[ωr

равен V = ωr sin α, где α – угол между векторами ω и r . Этот угол при движении по окружности равен 900 и sin 900 =1, т. е. V = ωR , где R – радиус окруж-

ности. Из решения задачи мы знаем ω= 3Bt2 . Следовательно, V = ωR = 3Bt2 R .

11

Тогда a

= dV = d(3Bt2R) = 6BRt . a

n

= V 2

= (ωR)2

= ω2R .

Из решения задачи

τ

dt

dt

R

R

следует,

что ω=

d (Bt2 )

= 3Bt

3

и an = (3Bt

2

)

2

R . Вектор полного линейного ус-

dt

2

dV

V

2

)

2

корения будет равен a

= aττ + ann =

dt

τ +

R

n = 3BRτ +(3Bt

Rn , а модуль

его запишется формулой a =

(3BR)2 + (3Bt2 )4 R2

.

Задача 3. Тело движется по закону V = αi +βxj . При t = 0,

x = y = 0 . Най-

ти: уравнение траектории, модуль скорости, вектор ускорения и модуль вектора ускорения, радиус-вектор и модуль радиуса-вектора.

Решение. При решении задачи необходимо воспользоваться знаниями, полученными из теории и при решении предыдущих задач. Анализируя уравнение, для вектора скорости можно записать

V =Vxi +Vy j +Vzk →V = αi +βxj .

Следовательно, Vx = α, Vy =βx , где Vx и Vy – проекции вектора скорости на

оси декартовой системы координат.

Для определения траектории движения тела необходимо найти координаты x и y . Используем уравнения кинематики

Vx = dÕ			x	t		t0 = αt , Õ = αt ,
		= α → dÕ =Vxdt → Õ = ∫dÕ = ∫αdt = αt													(1)
	dt		0	0										2
Vy = dÓ		y	t	t	βαtdt = αβt		2		t0	= αβt	2	Ó =βt			. (2)
	=βΧ → dÓ =Vydt →Ó = ∫dÓ = ∫βΧ dt = ∫
dt		0	0	0	2					2			2

Для определения траектории найдем выражение для t из уравнения (1) t =

x

и

Õ2

α

подставим в уравнение (2): Ó = αβ

→Ó =

β

Õ

2

. Таким образом, траекто-

α2

2α

2

рия

является

частью

параболы.

Модуль

скорости

равен

V =

V 2

+V 2

=

α2 + (βx)2

. Проекции вектора ускорения выразим через произ-

x

y

водные по времени от соответствующих проекций вектора скорости на оси де-

картовой

системы

координат.

ax = dVx

= d(α) = 0

,

dVy

d(βΧ )

dÕ

dt

dt

ay =

=

=β

=βα. Для нахождения радиуса-вектора воспользуем-

dt

dt

dt

Õ = αt , Ó =βt2 .

ся выражениями для его проекций, которые нашли выше:

2

12

						r				t2
Следовательно,							= Õi	+Ój	= αti +β	2 j	. Модуль радиуса-вектора равен
r = (αt)		2		β	t2	2
			+		2	.

Задача 4. Стальной шарик катится по круговому желобу радиусом R . Его

скорость изменяется по закону V = α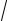S , где α – постоянная, S −путь, пройденный телом. Найти полное ускорение шарика и зависимость угла между направлениями полного ускорения и скорости от S .

Решение. По условию задачи скорость является функцией пути и для нахождения тангенциального ускорения необходимо использовать кинематические уравнения

a

= dV =

dV dS .

(1)

τ

dt

dt

dS

Скорость есть функция пути и производная от скорости по пути будет рав-

на

dV

= d(α S ) =

α

. Производная

dS =V равна скорости. Тогда тангенци-

dS

dS

2 S

dt

α2

α

α

альное ускорение из (1) будет равно a

=

V

=

α

S =

.

τ

2

S

2

S

2

Нормальное ускорение a

=

V 2

=

α2S

. Угол между направлением полного

n

R

R

a

2α2S

2S

ускорения и скоростью определяется из tgθ =

=

=

.

n

α2R

R

aτ

Полное ускорение a =

α4

+ α4S2

a2

+ a2

=

τ

n

4

R2

Задача 5. Твердое тело вращается вокруг неподвижной оси так, что его уг-

ловая скорость изменяется со временем по закону ω= At2 . Найти зависимость от времени угла поворота тела и его угловое ускорение.

Решение. Угловая скорость связана с углом поворота формулой

dϕ

→ dϕ = ωdt . Откуда находим

φ

t

t

2

At3

t

At

3

ω=

dt

ϕ = ∫dϕ = ∫ωdt = ∫At

dt =

0

=

.

3

3

0

0

0

Угловое ускорение связано с угловой скоростью соотношением

β =

dω

=

d(At2 )

= 2At .

dt

dt

13

Задачи для самостоятельного решения

1. Точка движется по закону r = Ati − Bt2 j +C(1−t3 )k. Найти V (t), V (t), a(t), a(t), угол ϕ между векторами V и a .

2.Частица движется по прямой со скоростью V = αt −βt2 . Найти путь, пройденный телом до остановки, и минимальную скорость тела Vmin .

3.Материальная точка движется по прямой по закону X = α +βt + γt2 .

Найти скорость и ускорение точки как функцию времени.

4. Радиус-вектор материальной точки меняется со временем по закону r = Ai − Btj +Ct2k . Найти вектор скорости (V ), модуль вектора скорости (V ), вектор ускорения (a), модуль вектора ускорения (a) .

5. Материальная точка движется по окружности радиусом R так, что S(t) = At + Bt2 . В какой момент времени t тангенциальное и нормальное ускорения будут равны?

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА

В основе динамики лежат законы Ньютона. Первый закон Ньютона формулируется следующим образом: всякое тело сохраняет состояние покоя или равномерного и прямолинейного движения (a = 0) , пока воздействие других

тел на это тело не заставит его изменить это состояние. Первый закон Ньютона указывает на то, что существуют такие системы отсчета, относительно которых тела сохраняют состояние покоя или равномерного прямолинейного движения, если на тела не действуют силы или сумма сил равна нулю. Такие системы отсчета называются инерциальными. Из этого следует, что первый закон Ньютона выполняется только в инерциальных системах отсчета.

Если на материальную точку действуют другие тела, происходит изменение состояния движения, тело выходит из состояния покоя или равномерного и прямолинейного движения, меняется скорость тела, т. е. тело приобретает ускорение.

Это воздействие характеризуется физической величиной, называемой силой (F) , которая является количественной характеристикой действия на тело

другого тела или физического поля. Если действовать одной и той же силой на разные тела то эти тела приобретают различные ускорения, т. е. различие в ускорениях обусловлено также свойством самих тел. Это свойство характеризуется особой величиной, называемой массой тела. Масса характеризует инертность тела, т. е. «сопротивляемость» тела воздействию силы.

14

Совокупность тел, движение которых рассматривается в данной задаче, называется механической системой. Импульс механической системы определяется как векторная сумма импульсов тел, образующих механическую систему:

p = p1 + p2 + p3 +... + pn = ∑n pi , pi = mVi .

i=1

Силы взаимодействия тел, входящих в механическую систему, называются внутренними силами. Силы, действующие на тела механической системы со стороны тел, не входящих в механическую систему, называются внешними силами.

Второй закон Ньютона позволяют установить закон изменения импульса. Второй закон Ньютона количественно связывает изменение движения механической системы с силами, вызывающими это изменение движения и гласит: скорость изменения импульса механической системы равен результирующей всех внешних сил, действующих на систему:

dpdt = Fрезвнешн (в дифференциальной форме)

или

∆p = t∫2 Fрезвнешнdt (в интегральной форме).

t1

Если масса постоянная и мы имеем дело с материальной точкой, то

dp = d(mV ) = m dV = ma , ma = ΣFi,внешн . dt dt dt

В таком виде второй закон Ньютона называется основным уравнением динамики материальной точки, или основным уравнением динамики поступательного движения.

Если на механическую систему внешние силы не действуют, то она называется замкнутой (изолированной). Для замкнутой системы Fрезвнешн = 0 и

dpdt = 0 . Равенство нулю производной говорит о том, что p = const , т. е. для

замкнутой системы выполняется закон сохранения импульса: импульс замкнутой механической системы остается постоянным. Закон сохранения импульса можно в некотором приближении применять и для незамкнутых систем, если результирующей внешних сил можно пренебречь. Это возможно, если эти внешние силы действуют мгновенно, т. е. промежуток времени действия внешней силы мал (удар, взрыв). Если результирующая внешних сил не равна нулю, но одна из ее проекций на декартову систему координат (напримерOX ) равна нулю, то проекция импульса системы на это направление сохраняется:

dpdtx = 0 → px = const .

Если имеется механическая система, состоящая из системы материальных точек, то центром масс (центром инерции) такой системы называется точка C ,

15

положение которой задается радиусом-вектором

r	= m1r1 + m2r2 +... + mnrn .
c		m1 + m2 +... + mn

Здесь rn – радиус-вектор нахождения материальной точки массой mn от-

носительно любой фиксированной точки системы.

Импульс системы материальных точек (твердого тела) равен произведению суммарной массы частиц системы m на скорость центра масс Vc системы

			dr			=	dV	d 2r
(твердого тела): p = mV		→V =	c ,	a	c		c =	c . Второй закон Ньютона
	c	c	dt				dt	dt2

для системы материальных точек через ускорение: mac = dVdtc = Fрезвнешн .

Третий закон Ньютона гласит: силы, с которыми взаимодействуют две материальные точки, равны по величине, противоположны по направлению и на-

правлены вдоль прямой, соединяющей эти точки: F1,2 = −F2,1 . Следует отме-

тить, что второй и третий законы Ньютона выполняются только в инерциальных системах отсчета.

Прежде чем приступить к решению задач, рассмотрим основные силы, действующие на тела.

Сила тяжести

Под воздействием притяжения к Земле все тела в отсутствие других сил, падают на Землю с одинаковым в данной точке Земли ускорением g , т. е. на тело

массой m действует сила тяжести F = mg . Сила тяжести приблизительно равна силе гравитационного взаимодействия тела и Земли: F = G Mmr2 (r = R3 + h) . Раз-

личие между этими силами обусловлено тем, что поверхность Земли не является инерциальной системой отсчета.

Сила сопротивления

Сила сопротивления (вязкого трения) возникает при движении твердого тела в жидкой или газообразной среде. Эта сила пропорциональна первой или

второй степени скорости тела в этой среде: Fc ~V ,V 2 .

Сила трения

Сила трения (сухого трения) возникает между поверхностями твердых тел как в случае попытки вызвать скольжение одного тела по другому (сила трения

покоя Fтр.0 ), так и при скольжении поверхности одного тела относительно поверхности другого тела (сила трения скольжения Fтр). Сила трения скольжения Fòð ≤ µN , где µ – коэффициент трения, зависящий от природы и состояния

16