ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

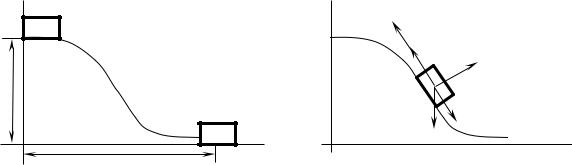
Задача 1. Тело массой m соскальзывает с пологой горки высотой h и длиной основания l и останавливается у ее подножия. Найти минимальную работу, которую надо затратить, чтобы затянуть тело на горку.

	1	x
		Fмин	N
	h
	2	mg	Fтр
	a	б

Для решения задачи необходимо ознакомиться с законом сохранения полной механической энергии, неконсервативными силами, динамическим уравнением второго закона Ньютона.

Решение. Для решения задачи используем закон изменения полной механической энергии с учетом неконсервативных сил. Рассмотрим два состояния системы: первое состояние – тело находится в начальном верхнем положении на горке и опустилось на основание горки (рис. а) и запишем закон изменения механической энергии для этого состояния

∆E = Eкон − Eнач = Aтр, Eнач = mgh, Eкон = 0 .

Минимальная работа будет выполнена, когда к телу приложена минимальная сила:

FминА ( минА = Fмин ).

Рассмотрим состояние, когда тело поднимается на горку (рис. б)). Составим динамическое уравнение второго закона Ньютона для этого случая и сделаем рисунок с обозначением направления всех сил (см. рис. б). Выберем систему координат и запишем проекции всех сил на оси этой системы координат. Горка пологая и зададим угол α , который она составляет с основанием. Сила, которая выполняет минимальную работу (Амин) , будет минимальной, когда тело пони-

мается с постоянной скоростью, т. е. ускорение тела равно нулю (a = 0) .

ma = Fмин + mg + N + Fтр → 0 = Fмин + mg + N + Fтр → Fмин = −(mg + N + Fтр) .

Для нахождения выполненной элементарной работы мы должны каждую из этих сил умножить скалярно на элементарное перемещение тела dr :

m(gdr ) → mgdr cosα = dAmg , (Ndr ) → Ndr cosα = AN = 0(cosα = 0), (Fòðdr ) → Fòðdr cosα = Aòð , dr sin α = dh

27

и интегрирование по dh даст нам минимальную работу:

h	h
Amg + Aтр = −∫mgdh − ∫mgdh = −2mgh .
0	0

Минимальная работа, затраченная на поднятие тела на горку, будет равна

AFмин = 2mgh .

X		m1
	x2
m	x1
1
k	0	Fупр
m2	•	m2
0		mg
a	б

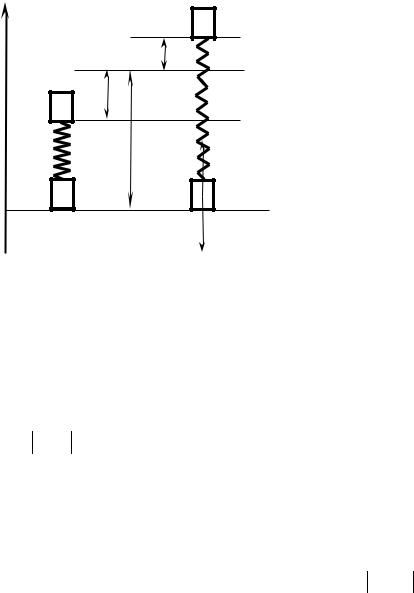
Задача 2. Два кубика массой m1 = m2 = m связаны пружиной, имеющей ко-

эффициент жесткости k , и поставлены вертикально. Насколько надо сжать пружину, чтобы при освобождении ее нижний кубик оторвался от подставки?

Решение. Рассмотрим два состояния системы: первое состояние (рис. а): пружина максимально сжата х1 = l −l0 . В этом состоянии система обладает энергией

E = E	+E	+ E	= 0 + mg(l	− x ) +	kõ2	,
					1
1	Ï í .ê Ï â.ê	Ï ï ð	0	1	2

где EПн.к – потенциальная энергия нижнего кубика, EПв.к – потенциальная энергия верхнего кубика, EПпр – потенциальная энергия сжатой пружины.

Второе состояние (рис б): пружина максимально растянута х2 = l2 −l0 . В этом состоянии система обладает энергией

E = E			+ E	+ Å	= 0 + mg(l				kx2
	Ï	í .ê						+ õ ) + 2 .
2			Ï â.ê	ï ð			0	2	2
Во втором состоянии на нижний кубик действуют силы mg, N, F упр . В
момент отрыва N = 0	для второго состояния можно записать динамическое
уравнение mg + N + F		= 0 , где F х = k				2	и в проекциях на ось OX (см. рис.)
упр				упр

28

mg + Fóï ð = 0 → kx2 = mg → õ2 = mgk .

Так как на систему не действуют неконсервативные силы, то закон сохранения энергии выполняется и можно записать

	kx2			kx2
mg(хl0 −	1	+	2 ) +	2	,
	1) + mg=l (x0			2
	2

		−mgx + kx12				= mg mg + k (mg )2,
			1	2			k 2 k
kx2	− 2хmgx	−3 m2g2	= 0,	1	= 2mg ±			4m2g2 ±12m2g2	= mg ± 2mg ,
1	1	k						2k	r

х1 = 3mgk .

Второе значение х2 = −х1 = − mgk соответствует растяжению (состояние 2) пружины.

Задача 3. Ведром массой m и объемом V зачерпывают воду, плотность которой равна ρ, на глубине h . Ведро висит на цепи, масса одного метра кото-

рой равна m0 . Какую работу надо совершить, чтобы вытянуть ведро с водой из колодца?

Решение. Определим приращение потенциальной энергии системы:

EП = E кон−Eнач .

Начальная потенциальная энергия системы будет определяться потенциальной энергией ведра с водой, находящихся на глубине колодца, и потенциальной энергий растянутой цепи:

Å

= −(m +ρV )gh − m g

h2

= 0 ,

2

í à÷

0

где ρV

масса воды,

величина

h задает центр масс цепи Y = − h

, а потенци-

2

c

2

альная

энергия цепи

определяется положением центра масс цепи и равна

m g

h

. Если за нулевой уровень принята поверхность Земли, то E

= 0 и

2

0

m0 h

кон

Å

= A = E

− E

= (m +ρV +

)gh .

Ï

êî í

í à÷

2

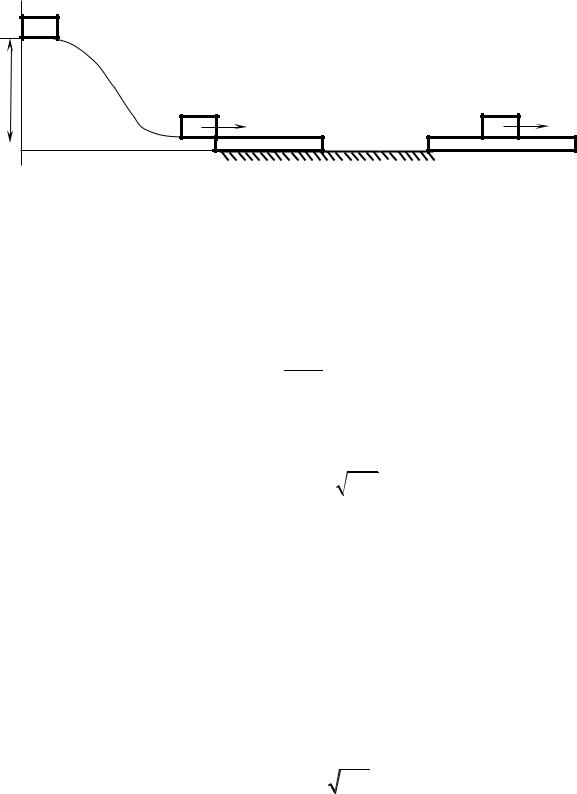
Задача 4. Тело массой m соскальзывает с гладкой горки высотой h и попадает на доску массой M . Доска лежит на гладкой поверхности. Найти работу силы трения между доской и телом, совершенную за все время движения тела по доске. Переход с горки на доску плавный.

29

1

	h	3	υ1
	2 υ

Решение. Воспользуемся законами сохранения энергии и импульса. Рассмотрим три состояния системы. Тело находится на вершине горки и покоится. В этом состоянии оно обладает потенциальной энергией

Eп = mgh .

Тело находится у подножия горки. Потенциальная энергия перешла в кинетическую энергию движения тела:

EK = mV2 2 ,

где V − скорость тела у подножия горки.

Так как горка гладкая, силы трения отсутствуют и выполняется закон сохранения энергии:

mgh = mV2 2 →V = 2gh .

Перед попаданием на доску у ее подножия тело приобрело импульс p = mV .

Тело находится на доске и они двигаются вместе как единое целое. В этом состоянии система тело доска обладает импульсом

и кинетической энергией

Так как на систему тело лы, то проекция px = p1x

откуда

p1 = (m + M )V1

EK1 = (m + M )V12 .

2

–доска не действуют в направлении OX внешние си-

=0 , т. е. выполняется закон сохранения импульса

p = p1 → mV = (m + M )V1,

V	=	m	V = m	2gh	.
1		m + M	m + M

Между телом и доской существует сила трения. Следовательно, изменение механической энергии равно работе силы трения и можно записать закон изменения полной механической энергии:

30

E

− E

= A

→

(m + M )V 2

mV 2

= A

K1

K

1 −

тр

2

2

тр

(m

А

= (m + M )

2gh

)2

− mgh = −

mM

gh.

тр

2

m + M

m + M

Задача 5. Санки длиной l0 скользят по гладкому льду со скоростью V и

выезжают на посыпанную песком дорогу. Продвинувшись по дороге на расстояние l = 3l0 , они останавливаются. Найти коэффициент трения µ дороги.

Для решения задачи необходимо проанализировать условия выполнения закона сохранения механической энергии.

Решение. Движение санок от начального до конечного положения можно разбить на четыре состояния (см. рис.). В первом состоянии тело скользит по гладкому льду со скоростью V и оно обладает в этом состоянии кинетической

энергией E1 = mV2 2 . В состоянии 4 тело останавливается и E4 = 0 . Запишем за-

кон изменения механической энергии: Eкон − Eнач = Aтр .

	υ	N1	N2	Fтр2	N	N = 0
		Fтр1
		•	x			x
		0			mg
	0	mg				3 0
состояние1		состояние 2			состояние 3	состояние 4

В состоянии 3 тело полностью скользит по шероховатой дороге, и сила трения в этом случае равна Fòð = µmg . Состояние 2 – это состояние, когда сан-

ки длиной l0 надвигаются на шероховатую дорогу. В этом состоянии на санки действуют четыре силы: сила тяжести mg , сила реакции опоры со стороны льда N1 , сила реакции опоры со стороны дороги N2 и сила трения Fтр2 , зависящая

только от силы реакции опоры со стороны дороги Fòð2 = µN2 . Здесь N2 = mg x . По l0

условию задачи движение по льду происходит без трения (Fòð1 = 0 ). Сила трения

Fтр2 является функцией x . Работа силы трения Fтр2						на участке 0−l0				равна
l0		l0	mg	mg l0		mg x2			l	mgl
Aòð2 = −∫µN2dx = −∫µ				xdx = −µ l	∫ xdx = −µ l				0	0	.
			l					Ι	0 = −µ	2
							2
0		0	0	0	0	0
На участке l	−3l	, равном 2l , сила трения постоянна и равна F = µmg
0	0			0						òð3

и работа сил трения на этом участке равна Aòð3 = −µmg2l0 . Запишем закон из-

31