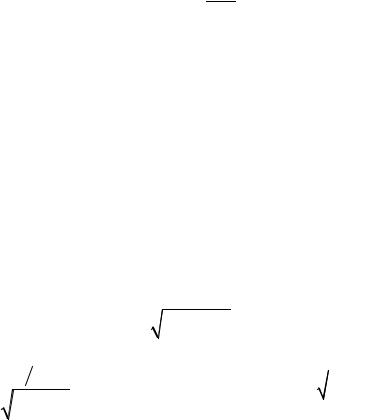
Отношение значений амплитуды затухающих колебаний, отличающихся

				A(t)
друг от друга на период T и равное					= eβt , называется декрементом за-
			A(t +T )
тухания, а ее логарифм логарифмическим декрементом затухания:
λ = ln	A(t)			=βT = T =		1	,
	A(t +T )
					τ	N

где τ = β1 – промежуток времени, в течение которого амплитуда затухания ко-

лебания уменьшилась в e раз и называемый временем релаксации; N − число колебаний, в течение которых амплитуда уменьшилась в e раз.

Добротностью колебательной системы называется безразмерная величина

	Q =	2π	=		2π	.
		1− e−2βT		1− e−2λ

При малых значениях λ колебания, почти не затухающие:

Q = λπ = βπT0 = ω2β0 ,

где T0 – период свободных колебаний, ω0 – циклическая частота свободных

колебаний.

Вынужденные колебания возникают, если кроме упругой силы и силы сопротивления среды на колеблющуюся систему действует добавочная периодически действующая сила. Уравнение движения (второй закон Ньютона) запишется в виде

m d 2x = −kx − r dx + F			(t) → d 2x + 2βdx + ω2x = F (t) .
dt2	dt	x	dt2	dt	0	x
Если вынуждающая	сила		изменяется	по гармоническому закону

Fx (t) = F0cosΩt , то для вынужденных установившихся колебаний амплитуда равна

A =			F0
					.
	m			)2 + 4β2Ω2
		(ω2	−Ω2
0

При резонансе амплитуда, соответствующая резонансной частоте, равна

	F0		m
A =					, а резонансная частота ω	рез	=	ω2	−β2	.
рез	2β ω2		−β2				0
	0

ВОЛНЫ

Тело называется упругим, а его деформация, вызываемая внешним воздействием, называется упругой деформацией, если она полностью исчезает после прекращения этого воздействия. Процесс распространения колебаний в упругой среде называется волной. Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные волны

56

связаны с объемными деформациями упругой среды и распространяются в любой среде – твердой, жидкой или газообразной. Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных направлению распространения волны. Поперечные волны связаны с деформациями сдвига упругой среды и распространяются только в кристаллических телах. Волна называется гармонической, если изменение состояния среды происходит по закону синуса или косинуса. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Геометрическое место точек, до которых доходит волна к моменту времени t , называется фронтом волны. По форме волнового фронта синусоидальная (косинусоидальная) волны делятся на плоские и сферические. Уравнение плоской синусоидальной волны, распространяющейся в направлении оси X ,

S = Asin(ωt − kX + α0 ) ,

где S – отклонение частицы среды от положения равновесия в момент времениt ; A −максимальное отклонение частицы среды от положения равновесия (амплиту-

да волны); ω= 2Tπ − круговая частота волны (T − период волны, ω = 2πν, ν –

собственная частота волны); k = 2λπ = VT2π = Vω − называется волновым числом;

λ =VT − расстояние, на которое распространяется синусоидальная волна за время равное периоду колебаний, называется длиной волны; α0 − начальная

фаза волны.

Уравнение сферической синусоидальной волны S = Ar sin (ωt − kr + α0 ).

	Дифференциальное волновое уравнение упругой волны	∆S =		1 ∂2S		, где
			V 2		∂t2

∆ = ∂22 + ∂22 + ∂22 – оператор Лапласа в декартовой системе координат.

∂x ∂y ∂z

Фазовая скорость упругих продольных VΙΙ = 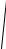Eρ и поперечных V = 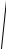Gρ

волн, где ρ− объемная плотность среды, E − модуль Юнга, G − модуль сдвига.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 1. Математический маятник с логарифмическим декрементом затухания λ0 поместили в среду, в

	dFc	R
		r •
		ω
		dFc

которой коэффициент сопротивления в n раз больше, чем в первой среде. Найти логариф- dr мический декремент затухания

маятника во второй среде.

57

Решение. В соответствии с условием задачи коэффициент сопротивления второй среды связан с коэффициентом сопротивления первой среды соотноше-

нием r = nr0 . Из теории известно, что 2β = mr → r = 2βm →β = nβ0 . Декремента затухания в первой среде равен

λ0 =β0T0			β0			2		2	2	2	2	2	2	2		2
	=						→ λ0ω0		−λ0β0		=β0	→ λ0ω0		=β0	(1	+ λ0 ) .	(1)
			ω2	−β2
			0		0

Используя значение декремента затухания во второй среде, путем математических преобразований получим значение декремента затухания во второй среде:

			λ2ω2	= nβ2 (1+ λ2 ) .				(2)
			0	0
Разделив (2) на (1), получим
λ2	= n2 (1+ λ2 )	→ λ2	+ λ2λ02 = n2λ02 + n2λ2λ02 → λ2 (1+ λ02 − n2λ02 ) = n2λ02 ,
λ02	1+ λ02				nλ0
			λ =
							.
					1+ λ02 (1− n2 )

Задача 2. Диск массой m и радиусом R подвесили на совершенно упругой нити за центр и привели в колебательное движение в горизонтальной плоскости вокруг вертикальной оси. Момент упругих сил нити равен M Fynp = αϕ . Сила

сопротивления внешней среды, действующая на единицу площади диска, равна Fc = ην. Найти период малых колебаний диска.

Решение. На диск действуют внешние силы, и колебания его будут затухающими. Для нахождения периода затухающих колебаний диска необходимо записать основное уравнение динамики вращательного движения с учетом всех сил, действующих на диск.

			Iβ = M F		+ M F .
				ynp		c
	В проекции на ось
			OZ	Iβ = −M F		− M F ,	(1)
					ynp	c
	где I =	mR2	− момент инерции диска. По условию задачи сила сопротивления
		2

среды приходится на единицу площади диска, и для нахождения силы сопротивления, действующей на весь диск, необходимо выделить элементарную площадь диска, найти элементарную силу сопротивления с учетом того, что ν = ωr и путем интегрирования найти полный момент силы Fc.

dFc = ηνdS = ηωr2πrdr .

58

Момент силы будет равен

R

dMFc = rdFc = rηω2πr2dr = 2πηωr3dr → MFc = ∫2πηωr3dr =

0

R		4	= ωπηR				4
= 2πηω∫r3dr = 2πηωR								,
0	4					2
				d 2
	β =				κ	, ω=			dϕ	.
				dt	2				dt

Уравнение (1) запишем в виде

I

d 2ϕ

= −

πηR4 dϕ

− αϕ → I

d 2ϕ

+

πηR4 dϕ

+ αϕ = 0

,

dt2

2

dt

dt2

2

dt

d 2ϕ

+

πηR4 dϕ

+

α

ϕ = 0 →

d

2ϕ

+

πηR4

dϕ

+

2α

ϕ =

0 .

dt2

2I

dt

I

dt2

m

dt

mR2

2α

πηR2

πηR2

2π

2

2α

2

2

Откуда ω0

=

,

β =

, ω=

(

)

−(

)

,

T =

.

mR2

2m

mR2

2m

π

Fóï ð

•

mg

Fx

Задача 3. Тело подвешено на пружине и под действием внешней вертикальной силы Fx = F0cosωt совершает установив-

шиеся движения по закону x = Acos(ωt − ϕ). Найти работу силы Fx за период T колебаний.

Решение. Колебания вынужденные и под действием вынуждающей силы Fx тело совершает работу

A = ∫Fxdx .

(1)

Уравнение установившегося движения тела задано и, продифференцировав это выражение, получим

dx = −aωsin(ωt −ϕ).

Подставим все эти значения в (1) и, используя формулы приведения, найдем работу A:

59

T T

A = −∫aωF0 cosωt sin(ωt − ϕ)dt = −aωF0 ∫cosωt(sin ωtcosϕ −cosωt sin ϕ)dt =

0

0

T

= −aωF0

∫(sin ωt cosωt cosϕ −cos2 ωt sin ϕ)dt =

0

= −aωF0

T

(

sin 2ωt

cosϕ −

1

+cos2ωt

sin ϕ)dt =

∫

2

2

0

aωF

cos2ωt cosϕ +

aωF

aωF

ΙT0

=

aωF

T sin ϕ =

=

0

2

0 t sin ϕ +

0 sin 2ωt sin ϕ

0

4ω

4ω

2

= 2πaωF0 sin ϕ = πaF0 sin ϕ.

2ω

Задача 4. От источника волн с частотой ν распространяется синусоидальная волна с начальной фазой α0 = 0, скоростью V и амплитудой A. Определить

длину волны, фазу и ускорение точки, находящейся на расстоянии x от источника в момент времени t .

Решение. В общем случае уравнение синусоидальной волны имеет вид

S = Asin(ωt − kx + α0 ) ,

где ω = 2πν – циклическая (круговая) частота колебаний; k = 2λπ = VT2π = Vω −

волновое число; α0 – начальная фаза волны.

Тогда уравнение синусоидальной волны с учетом того, чтоα0 = 0 , запишется

			2πν			2πν			x
	в виде S = Asin	2πνt −	V	x	, где ϕ = ωt − kx = 2πνt −		x = 2πν(t −			) – фаза
						V		V

волны, а λ =VT = V .
	ν
Ускорение точки найдется как вторая производная от уравнения волны
	d 2S		2	2		2			x
a =	dt	2	= −Aω sin(ωt − kx) = −A4π		ν		sin	2πν t −		.
									V

Задача 5. Плоская волна распространяется со скоростью V . Период колебаний точек среды T . Найти разность фаз колебаний между точками, находящимися на расстоянии ∆x друг от друга.

Решение. Поскольку необходимо найти разность фаз одной и той же волны, то начальная фаза и циклическая частота будут одинаковыми для всех точек волны, и разности фаз в точке 1 в точке 2 запишутся как

60