6____2004

Тема 4. Прямая в пространстве

4.1. Уравнение прямой в пространстве

Рассмотрим произвольную прямую, обозначим ее буквой a . Обозначим

через α1	и	α2	какие-нибудь две различные плоскости, пересекающиеся по
прямой	a	и	предположим, что уравнения	этих	плоскостей будут:
A1 x + B1 y +C1 z + D1 = 0 и A2 x + B2 y +C2 z + D2				= 0 .	Так как прямая a

представляет собой пересечение плоскостей α1 и α2 , то она определяется системой двух уравнений:

	A x + B y +C z + D				=0,	(4.1)
	1	1	1	1
A2 x + B2 y +C2 z + D2 =0.

Поставим задачу: всегда ли два уравнения первой степени совместно определяют некоторую прямую? Очевидно, это будет только в том случае, когда соответствующие им плоскости не параллельны и не совпадают друг с другом, т.е. когда нормальные векторы этих плоскостей n1 ={A1 , B1 ,C1} и

n2 ={A2 , B2 ,C2 } не коллинеарны. Два уравнения вида (4.1) совместно определяют прямую в том и только в том случае, когда коэффициенты A1 , B1 , C1 одного из них не пропорциональны коэффициентам A2 , B2 , C2 другого.

4.2. Направляющий вектор прямой. Канонические уравнения прямой. Параметрические уравнения прямой

Рассмотрим произвольную прямую. Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой. Указанные векторы называются направляющими именно потому, что любой из них, будучи задан, определяет направление прямой.

Направляющий вектор прямой будем обозначать буквой l , его координаты – m, n, p : l ={m, n, p}.

Введем уравнение прямой, проходящей через заданную точку M 0(x0 ,y0 ,z0 ) и имеющей данный направляющий вектор l ={m, n, p}.

61

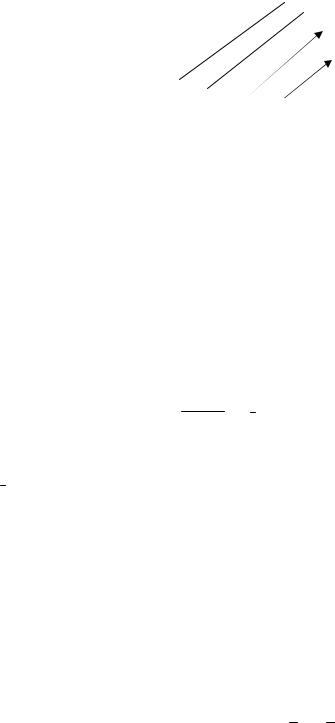
Пусть M(x,y,z) – произвольная («текущая») точка прямой (рис. 4.1).

M

M0

рис. 4.1

Вектор

={x − x0 , y − y0 ,

z − z0 }

коллинеарен направляющему вектору

M 0 M

={m, n, p} . Следовательно,

координаты вектора

пропорциональны

l

M 0 M

координатам вектора

:

l

x − x0

=

y − y0

=

z − z0

(4.2)

m

n

p

Этим соотношениям удовлетворяют координаты каждой точки M(x, y, z) , лежащей на рассматриваемой прямой, напротив, если точка M(x, y, z) не

лежит на прямой, то ее координаты не удовлетворяют соотношениям (4.1), так как в этом случае векторы M 0 M и l не коллинеарны и координаты их не

пропорциональны. Таким образом, уравнения (4.1) представляют собой уравнения прямой, проходящей, через точку M 0(x0 ,y0 ,z0 ) в направлении

вектора l ={m, n, p} .

Уравнение прямой (4.2) будем называть каноническими.

Пусть некоторая прямая задана двумя общими уравнениями:

A1 x + B1 y +C1 z + D1 = 0, .A2 x + B2 y +C2 z + D2 = 0

Покажем, как составить канонические уравнения этой прямой. Обозначим плоскости, определяемые данными уравнениями, через α1

(4.3)

и α2 ,

нормальные векторы этих плоскостей через n1 и n2 .

Для составления канонических уравнений данной прямой, нужно: найти произвольную ее точку M 0(x0 ,y0 ,z0 ) ; для этого надо задать численное

62

значение одной из известных координат x0 ,y0 ,z0 и подставить его вместо

соответствующей переменной в уравнения (4.3); после этого две остальные координаты определяются из уравнений (4.3) путем их совместного решения;

найти направляющий вектор l ={m, n, p}. Так как данная прямая определена пересечением плоскостей α1 и α2 , то она перпендикулярна к каждому из

векторов n1 и n2 . Поэтому в качестве вектора l можно взять любой вектор, перпендикулярный к векторам n1 и n2 , например, их векторное

произведение:

=[

1;

2 ]. Поскольку координаты векторов

1 и

2

известны:

l

n

n

n

n

1 ={A1 , B1 ,C1},

2 ={A2 , B2 ,C2 }, для вычисления координат

вектора

n

n

достаточно применить формулу для нахождения координат векторного произведения.

4.3.Некоторые дополнительные предложения и примеры

Ваналитической геометрии часто требуется составить уравнения прямой, зная две ее точки. Решим эту задачу в общем виде, считая данными две произвольные точки: M1(x1,y1,z1 ) и M 2(x2 ,y2 ,z2 ) .

Для решения задачи достаточно заметить, что в качестве направляющего вектора рассматриваемой прямой можно взять вектор l = M1M 2 ; отсюда m = x2-x1 ; n = y2-y1 ; p = z2-z1 , окончательно получим

x − x1			=	y − y1			=	z − z1
x	2	− x		y	2	− y		z	2	− z
		1				1				1

Это и есть искомые (канонические) уравнения прямой, проходящей через две данные точки: M1(x1,y1,z1 ) и M 2(x2 ,y2 ,z2 ) .

4.4. Угол между двумя прямыми

Углом между двумя прямыми в пространстве называют любой из углов,

образованный двумя прямыми, проведенными из одной точки, параллельно данным прямым. Если прямые параллельны, то угол между ними считается равным нулю или π .

Пусть даны уравнения двух прямых:

x − x

y − y

z − z

x − x2

=

y − y2

=

z − z2

1

=

1

=

1

;

.

m2

n2

p2

m1

n1

p1

63

Обозначим угол между прямыми через α , а угол между их направляющими векторами l1 и l 2 – через ϕ. При этом

	cosϕ =					l	1		l		2													(4.4)
			| l1 || l 2 |
Так как α =ϕ или α =π −ϕ, то cosα = ±cosϕ . Следовательно,
																1		2
	cosϕ = ±													l			l							(4.5)
								| l1 || l 2 |
или в координатной форме:
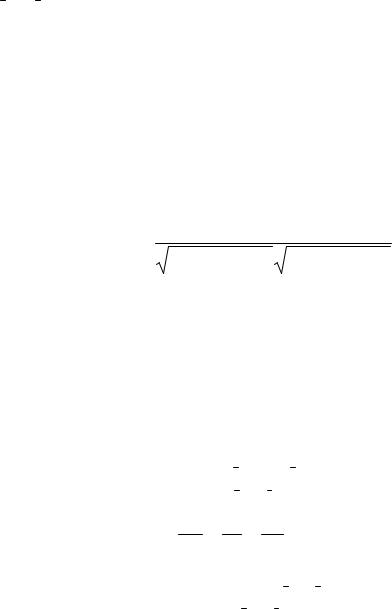
cosα = ±		m1m2 +n1n2 + p1 p2																						(4.6)
	m2	+n2	+ p2															m2				+n2	+ p2
	1	1						1										2				2	2

Формулы (4.5) и (4.6) являются формулами для определения угла между двумя прямыми в пространстве.

4.5. Условия параллельности и перпендикулярности двух прямых в пространстве

Для того, чтобы две прямые были параллельны, необходимо и достаточно, чтобы их направляющие векторы l1 и l 2 были коллинеарны, т.е. соответствующие координаты векторов l1 и l 2 были пропорциональны:

m1 = n1 = p1 . m2 n2 p2

Для того, чтобы прямые были перпендикулярны между собой, необходимо и достаточно, чтобы направляющие их векторы l1 и l 2 были ортогональными. Условие ортогональности двух векторов l1 и l 2 :

m1m2 + n1n2 + p1 p2 =0 .

Пример 1.

Найти уравнения прямой, проходящей через точку M (3,2,−1) перпендикулярно двум прямым:

a

:

x −1

=

y −7

=

z + 4

a

2

:

x +3

=

y +5

=

z −9

.

1

2

−3

5

4

1

−2

Составим уравнение любой прямой, проходящей через точку M :

64

		x −3	=	y −2		=	z +1
		m
					n		p
Используя	условие перпендикулярности				искомой			прямой		к прямой	a1 , а затем к
прямой a2	получим	2m −3n +5 p = 0
					−2 p = 0
		4m + n
Из этой однородной системы линейных уравнений с неизвестными											m, n, p найдем
отношения неизвестных:
	−3	5 5				2 2			−3	1: 24 :14
	m : n : p =		:				:		=
	1	−2 −2				4 4			1
Подставляя в уравнения прямой вместо					m, n, p			пропорциональные им величины,

получим искомые уравнения:

x 1−9 = y 24+13 = z 14−15 .

65

Тема 5. Плоскость и прямая в пространстве

5.1. Пересечение прямой и плоскости

Точкой пересечения прямой, не лежащей в плоскости α , и плоскости α

называется общая точка, принадлежащая и прямой, и плоскости.

Чтобы найти точку пересечения прямой

l :	x − x0	=	y − y0		=	z − z0		(5.1)
						p
	m			n
и плоскости	Ax + By +Cz + D = 0,							(5.2)
α :
запишем параметрические уравнения прямой (5.1):
	x = x0 +mt,
				+nt,				(5.3)
	y = y0
				+ pt,
	z = z0

и подставим в уравнение плоскости (5.2). Получим значение t и затем из системы (5.3) получим координаты (x0 , y0 , z0 ) точки пересечения прямой и

плоскости.

Пример 1.

Найти точку пересечения прямой	x −12	=	y −9	=	z −1		и плоскости 3x +5 y − z −2 = 0.
	4				1
		3
Уравнение прямой перепишем в параметрическом виде
	x = 4t +12,
	y =3t +9,
		z =t +1

и подставим в уравнение плоскости 3(4t +12) +5(3t +9) −(t +1) −2 = 0,

отсюда t = −3. Подставив в (5.3), получим, что координаты точки пересечения прямой и плоскости есть

x = 0,y = 0,

z = −2.

66

5.2. Угол между прямой и плоскостью

Угол между прямой (5.1) и плоскостью (5.2) вычисляется по формуле:

sin ϕ = ±

Am + Bn +Cp

A2 + B2

+C 2

m2

+ n2 + p2 .

Условие параллельности прямой (5.1) и плоскости (5.2):

Am + Bn +Cp = 0.

Условие перпендикулярности прямой (5.1)

и плоскости (5.2):

A

=

B

=

C

.

Пример 2.

m

n

p

Написать уравнение прямой l, проходящей через

точку

M 0 (3,−4,2) и

перпендикулярной плоскости α : 2x −4 y +7z −4 = 0 .

Канонические уравнения прямой l имеют вид

x − x0

=

y − y0

=

z − z0

.

n

m

p

В качестве x0 , y0 , z0 берем координаты точки M 0 : x0 = 3 ,

y0 = −4 , z0

= 2 .

Так как прямая перпендикулярна плоскости, в качестве направляющего вектора прямой l ={m, n, p} берем нормальный вектор плоскости n ={2,−4,7} .

Получим уравнения

x 2−3 = y−+44 = z −7 2 .

5.3. Уравнение плоскости, проходящей через прямую и точку

Пусть даны прямая	l и точка M 0 = (x0 , y0 , z0 ) , требуется записать
уравнение плоскости α,	проходящей через эти точку и прямую. Сначала
запишем уравнение плоскости, проходящей через точку M 0 :
α :	A(x − x0 ) + B( y − y0 ) +C(z − z0 ) = 0.

Нормальный вектор n ={A, B, C} плоскости α можно найти как векторное произведение направляющего вектора l прямой l и вектора M1 M 0 , где M1 – произвольная точка прямой l, М0 – данная точка т. е. n =[l , M1M 0 ] .

67

Пример 3.

Написать уравнение плоскости, которая проходит через точку (3, 1, −2) и прямую

x −4

=

y −3

=

z

.

5

2

1

Выпишем уравнение плоскости, проходящей через точку M 0

= (3, 1,

−2) :

A(x −3) + B( y −1) +C(z + 2) = 0.

Возьмем точку M1

на прямой

x −4

=

y −3

=

z

, например,

M1 = (4,

3, 0). Тогда

2

5

1

вектор M1 M0 ={−1,

−2, −2} . Нормальный вектор плоскости есть

i

j

k

n =[e , M1M0 ] =

5

2

1

= −2

+9

−8

={−2,9, −8} .

k

i

j

−1 −2 −2

Уравнение плоскости, которая проходит через точку

(3,

1, −2)

и через прямую

x −4

=

y −3

=

z

, есть −2(x −3) +9( y −2) −8(z + 2) = 0,

т.е. −2x +

9 y −8z −28 = 0.

5

2

1

5.4. Уравнение плоскости, проходящей через две параллельные прямые

Задача о нахождении уравнения плоскости, проходящей через две параллельные прямые, сводится к задаче, описанной в пункте 5.3, если в качестве точки M0 взять точку на прямой l2 , в

качестве точки М1 , взять точку на прямой l1 , а в качестве вектора l − направляющий вектор прямой l1 .

Пример 4.

Написать уравнение плоскости α , проходящей через прямые

l

:

x −2

=

y +1

=

z −1

1

4

3

−2

и

x +1

y +3

z −9

l

2

:

=

=

.

−8

−6

4

Направляющие векторы l1 = {4,3,−2} и l2 = {−8,−6,4} прямых l1 , l2 параллельны,

	так как	4	=	3	=	−2	.
		−8		−6		4

68

Выбираем точку M 0 (−1, −3, 9)

на прямой l2 ,

точку M1 (2, −1, 1) на прямой l1 . Тогда

={−3, −2, 8} ,

=

={4,

3, −2} .

M1M 0

l

l1

i

j

k

=[

,

] =

4

3

−2

= 20i −26

+

.

n

l

M1M 0

j

k

−3

−2

8

Тогда,

согласно (3.2), уравнение плоскости α будет иметь вид

20(x +1) − 26( y +3) + (z −9) =0

или

20x −26 y + z −67 = 0.

5.5. Уравнение плоскости, проходящей через две пересекающиеся прямые

Найти уравнение плоскости, проходящей через пересекающиеся прямые, также можно с помощью рассуждений, приведенных в пункте 5.3. При этом в качестве точки M0 берем произвольную точку,

лежащую на одной из прямых, а в качестве нормального вектора n векторное произведение

направляющих векторов прямых l1 и l2 : n =[l1 , l2 ].

Пример 5.

Написать уравнение плоскости, проходящей через прямые:

l :

x + 2

=

y

=

z −1

,

1

2

−3

4

l2

:

x −3

=

y −1

=

z −7

.

3

4

2

Проверим, будут ли прямые l1 ,

l2

пересекаться.

Для этого запишем уравнения прямой l1 в параметрической форме:

x = 2t − 2,

y = −3t,

(5.4)

z = 4t +1,

и подставим вместо x, y, z

в уравнение прямой l2 :

l2 :

2t −5

=

−3t −1

=

4t −6

.

2

3

4

Решая уравнения

69

2t −5	=	−3t −1		и	−3t −1		=	4t −6	,
3		4			4			2

получим, что они имеют одинаковые решения t =1, и, следовательно, прямые l1 и l2 пересекаются.

Для нахождения точки пересечения прямых l1 и l2 , подставим t =1 в уравнения (5.4).

Получим

x = 0, y = −3,

z =5.

Далее, для того, чтобы написать уравнение плоскости α , берем, например, точку

M0 (0, −3,5) (в качестве этой точки можно выбрать также точку M1 (−2, 0,1) , лежащую на прямой l1 , или точку M2 (3,1,7), лежащую на прямой l2 ) и нормальный вектор

n =[l1, l2 ], где l1 ={2, −3, 4} – направляющий вектор прямой l1 ,

l2 ={3, 4, 2} – направляющий вектор прямой l2 .

Тогда

i j k

n = 2 −3 4 = −22i +8 j +17k. 3 4 2

Уравнение плоскости α , согласно (3.2) будет иметь вид:

−22(x −0) +8( y +3) +17(z −5) = 0,

или, после упрощения,

22x −8 y −17z +61 = 0.

5.6. Расстояние от точки до прямой в пространстве

Для того, чтобы найти расстояние от точки P = (x1 , y1 , z1 ) до прямой

	l :	x − x0	=	y − y0			=		z − z0	,
		m
					n				p
проведем	через		P			плоскость					α ,
перпендикулярную		прямой			l .			Точка Q			есть

пересечение прямой l и плоскости α . Искомое расстояние от точки P до данной прямой будет равно расстоянию от точки P до точки Q .

70