Теор.вер

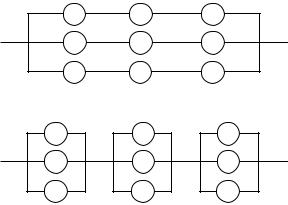
Висновки обгрунтувати обчисленням.

A1	A2	A3
A1	A2	A3
A1	A2	A3
	а
A1	A2	A3
A1	A2	A3
A1	A2	A3

б

Рис. 1.8

1.44.Через канал зв’язку, який складається з передавача, ретранслятора та приймача, передаються сигнали “0” та “1”. Унаслідок перешкод ці сигнали можуть спотворюватися. На ділянці передавач–ретранслятор “1” не спотворюється з імовірністю 0,8, а “0” не спотворюється з імовірністю 0,85. На ділянці ретранслятор–приймач імовірності цих подій відповідно дорівнюють 0,9 та 0,7. Знайти ймовірності подій: 1) кодова комбінація “10”, надіслана передавачем, прийнята без спотворення;

2)передали комбінацію “10”, а прийняли два однакові символи.

1.45.Студент написав n листів, запечатав їх у конверти, а потім на кожному конверті навмання написав різні адреси. Яка ймовірність того, що принаймні на одному конверті буде написана вірна адреса?

1.46.Із урни, яка містить дві білі та чотири чорні кулі, два гравці по черзі виймають кулі, не повертаючи їх знову в урну. Виграє той, хто першим витягне білу кулю. Яка ймовірність події А={виграє той, хто почав першим}?

1.47.Два гравці домовились, що виграш одержує той, хто виграє певне число партій. Гра була перервана тоді, коли першому гравцю залишалось до виграшу m партій, а другому – n партій. Як

поділити ставку, якщо ймовірність виграшу однієї партії для кожного гравця однакова і дорівнює 0,5? (Задача де Мере).

1.4. Формула повної ймовірності. Формула Байєса

Нехай події H1, H2,..., Hn утворюють повну групу подій деякого стохастичного експерименту. Назвемо ці події гіпотезами експерименту. Тоді ймовірність будь-якої події А цього стохастичного експерименту обчислюється за формулою повної

ймовірності

n
P( A) P(Hi )P( A / Hi ).	(1.3)

i 1

Імовірності P H i , i = 1, 2,..., n часто називають апріорними.

Нехай відомо, що в експерименті відбулася подія А. Її поява зумовить переоцінку апріорних імовірностей гіпотез. Формула Байєса дає можливість зробити цю переоцінку, тобто обчислити

апостеріорні ймовірності P(Hi /A):

P(Hi / A)	P(Hi )P( A / Hi )	, i 1, 2,..., n. (1.4)
	n
	P Hk P( А / Hk )

k 1

Приклади розв’язання задач

Задача 1.9. На стадіон прибуло десять спортсменів, з яких чотири виконували вправи повністю, п’ять – на 80 % і один виконував вправи наполовину. Яка ймовірність виконання вправ першим викликаним спортсменом?

Розв’язання. Вводимо гіпотези: H1={викликаний спортсмен – з числа тих, які повністю виконували вправи}, H2 ={викликаний спортсмен – з числа тих, які виконували вправи на 80 %}, H3={викликаний спортсмен – з числа тих, які виконували вправи тільки наполовину}. З умови задачі зрозуміло, що P(H1) = 0,4; P(H2) = 0,5; P(H3)=0,1. Нехай подія A={виконання вправ першим викликаним спортсменом}, тоді за умовою задачі P(A/H1) = 1,

P(A/H2) = 0,8, P(A/H3) = 0,5. За формулою (1.3)

P(А) = 0,4+0,4+0,05 = 0,85.

Задача 1.10. Через перешкоди система виявлення літака може давати помилкові дані про наявність цілі з імовірністю 0,05, а за наявності цілі система виявляє її з імовірністю 0,9. Імовірність появи літака в зоні роботи системи дорівнює 0,25. Надійшов сигнал про наявність цілі. Яка ймовірність помилки?

Розв’язання. Введемо гіпотези:

H1 ={у зоні роботи системи з’явився літак};

H2 ={відсутність літака в зоні роботи системи}.

За умовою задачі P(H1) = 0,25, тоді P(H2) = 0,75. Нехай подія A = {надійшов сигнал про наявність літака}. Тоді P(A/H1) = 0,9; P(A/H2)=0,05. Помилка буде тоді, коли система дала сигнал про наявність цілі, але літака в зоні роботи системи не було. Отже, треба знайти P H2 / A . За формулою Байєса (1.4) маємо

	P H 2	/ A			P(H 2 )P( A / H		2 )
			P(H1 )P( A / H1 ) P(H 2 )P( A / H 2 )
					0,05 0,75			1	.
					0,9 0,75 0,05
		0,25					7

Задачі

Група А

1.48.На вогневій позиції знаходиться тригарматна батарея. Імовірність влучення в ціль з першої та другої гармат дорівнює 0,4,

аз третьої – 0,3. Яка ймовірність влучення в ціль при одному пострілі, якщо стрільба рівноможлива з кожної гармати?

1.49.На трьох автоматичних лініях виготовляються однотипні деталі. Внаслідок розладу верстатів можливий випуск бракованої продукції першою лінією з імовірністю 0,02, другою – з імовірністю 0,01, а третьою – з імовірністю 0,05. Перша лінія дає 70 % усієї продукції, друга – 20 %, а третя – 10 %. Яка ймовірність того, що випадково вибрана деталь буде бракованою?

1.50.У зоні ППО об’єкта розгорнуто три РЛС, кожна з яких може вийти з ладу з імовірністю 0,3. Імовірність пропуску цілі при роботі однієї РЛС дорівнює 0,5, двох – 0,3, трьох – 0,1. Яка ймовірність пропуску цілі?

1.51. Літак-розвідник, який виконує бойове завдання, повинен два рази пройти зону ППО противника (туди і назад).

У зоні ППО його з імовірністю 0,5 не атакують винищувачі, з імовірністю 0,3 атакує один винищувач, з імовірністю 0,2 – два винищувачі. Кожен винищувач окремо вражає літак з імовірністю 0,4. Яка ймовірність того, що літак виконає бойове завдання?

1.52.Є дві партії деталей з 12 і 10 виробів, причому в кожній партії одна деталь є бракованою. Навмання взяли деталь з першої партії і переклали в другу, після чого виймають будь-яку деталь з другої партії. Яка ймовірність того, що з другої партії буде вийнята бракована деталь?

1.53.У кожний момент часу працює тільки один з трьох блоків приладу. Встановлено, що перший блок працює 40 % усього часу, другий – 35 %. Надійність блоків за час T відповідно дорівнює 0,95; 0,92 та 0,9. Прилад вимикається через несправність одного з блоків. Знайти ймовірність несправності в кожному з блоків, якщо прилад вимкнено.

1.54.Телеграфне повідомлення складається з сигналів “крапка” та “тире”. Статистичні властивості перешкоди такі, що

	спотворюють у середньому	2	повідомлень “крапка” та	1
		5		3

повідомлень “тире”. Відомо, що серед сигналів, які передаються, “крапка” та “тире” зустрічаються у відношенні 5:3. Знайти ймовірності подій: 1) прийнято сигнал “крапка”; 2) надіслали сигнал “тире”, а прийняли сигнал “крапка”.

1.55.У групі з 10 студентів, які прийшли на іспит, три підготовлені відмінно, чотири – добре, два – задовільно та один – погано. У білетах є 20 запитань. Відмінно підготовлені студенти можуть відповісти на всі 20 запитань, добре підготовлені – тільки на 16 запитань, задовільно підготовлені – тільки на 10, погано підготовлений студент – тільки на п’ять. Викликаний навмання студент відповів на три запитання. Знайти ймовірність того, що цей студент підготовлений: 1) відмінно; 2) погано.

1.56.Відомо, що 96 % виготовленої продукції задовольняє стандарт. Спрощена схема контролю визнає придатною стандартну

продукцію з імовірністю 0,98 та нестандартну – з імовірністю 0,05. Яка ймовірність того, що продукція, яка пройшла спрощений контроль, задовольняє стандарт?

1.57. У піраміді знаходяться 10 карабінів, які складають чотири групи, що різняться своїми бойовими якостями. До першої групи належать два карабіни, до другої – чотири, до третьої – три, до четвертої – один карабін. Імовірність влучення в мішень з карабіна першої групи дорівнює 0,92, другої – 0,8, третьої – 0,75, четвертої – 0,5. Стрілець бере навмання один карабін і робить один постріл. 1. Яка ймовірність того, що стрілець влучить у мішень?

2. Стрілець схибив. Яка ймовірність того, що він стріляв з карабіна третьої групи?

Група Б

1.58.Винищувач атакує літак противника й випускає по ньому три ракети з різних дистанцій. Ракети влучають у ціль незалежно одна від одної. Імовірність влучення ракети з першої дистанції дорівнює 0,4, з другої – 0,5, з третьої – 0,6. Імовірність ураження літака при влученні у нього однієї ракети дорівнює 0,2; двох – 0,6; трьох – 1. Яке найбільше число влучень у літак, якщо він у результаті атаки уражений?

1.59.Для пошуків літака направили десять гелікоптерів. Кожний гелікоптер може бути використаний в одному з двох районів, де літак може знаходиться з імовірностями 0,8 та 0,2. Як треба розподілити гелікоптери по районах пошуків, щоб імовірність виявлення літака була найбільшою? Відомо, що кожний гелікоптер виявляє літак, який знаходиться в районі пошуку, з імовірністю 0,2. Пошук здійснюється кожним гелікоптером незалежно від інших. Яка ймовірність виявлення літака при оптимальному пошуку?

1.60.В університеті n студентів, з яких nk (k = 1, 2, 3)

навчаються k -й рік. Серед двох навмання відібраних студентів виявилося, що один з них навчається довше від другого. Яка ймовірність того, що цей студент навчається третій рік?

1.61. Виконується посадка літака на аеродром. Якщо дозволяє погода, пілот здійснює посадку, спостерігаючи за

аеродромом візуально. У цьому випадку ймовірність благополучної посадки дорівнює p1 . Якщо аеродром затягнуло низькою

хмарністю, то пілот здійснює посадку літака за допомогою приладів. Надійність приладів “сліпої” посадки дорівнює P . Якщо прилади “сліпої” посадки спрацювали нормально, то літак сідає з тією ж імовірністю p1 , що й при візуальній посадці. Якщо прилади

“сліпої” посадки не спрацювали, то пілот може посадити літак з імовірністю p1 p1 . 1. Знайти повну ймовірність посадки літака,

якщо відомо, що в k % всіх випадків посадки аеродром затягнутий низькою хмарністю. 2. Відомо, що літак приземлився благополучно. Яка ймовірність того, що пілот користувався приладами “сліпої” посадки?

1.62.Маємо три урни: у першій з них а білих куль і b чорних; у другій – c білих куль і d чорних; у третій – тільки k білих. Навмання вибирають одну урну і виймають з неї кулю. Ця куля виявилася білою. Знайти ймовірності того, що ця куля витягнута:

1)з першої урни; 2) з другої урни; 3) з третьої урни.

1.63.Серед n осіб розігрують m n виграшів витягуванням n квитків. Чи однакові шанси виграшу для будь-якого з гравців? Чи вигідно тягнути квиток на початку розіграшу?

1.5.Послідовні незалежні випробування. Схема Бернуллі

Розглянемо n незалежно проведених дослідів (випробувань) з двома результатами: успіх та невдача. Схема незалежних випробувань, у якій кожне випробування закінчується двома результатами, називається схемою Бернуллі. Нехай імовірність

успіху в кожному	досліді дорівнює		p , а невдачі – відповідно
q 1 p . Тоді ймовірність того, що в			n дослідах рівно	m разів
буде успіх, обчислюється за формулою Бернуллі:
P	m Cm pmqn m ,	m 0, 1,...,n.		(1.5)
n	n
Число m0 , при якому Pn m		набуває найбільшого значення,

називається найбільш імовірним числом успіхів. Воно дорівнює:

1) np p , якщо np p – неціле число; 2) якщо np p – ціле

число, то існують два найбільш імовірних числа m01 np q та m02 np p .

Якщо n достатньо велике, а			p – достатньо	мале число,
наприклад, n>100 і p<0,01 або			np 20 , то	найчастіше
використовують асимптотичну формулу Пуассона:
P m	a m	e a , де a np.		(1.6)
n	m!
			Ф z pz q n
Функція комплексної змінної				називається

генератрисою у схемі Бернуллі. Коефіцієнт при z m у розкладі генератриси за біномом Ньютона дорівнює Pn m .

Приклади розв’язання задач

Задача 1.11. Спортсмен п’ять разів стріляє по мішені. Імовірність влучення в мішень при одному пострілі дорівнює 0,4. Для одержання заліку необхідно влучити не менше трьох разів. Яка ймовірність одержання заліку? Яке найбільш імовірне число влучень у мішень?

Розв’язання. Нехай подія A = {залік одержано}. За теоремою додавання ймовірностей для незалежних подій, маємо:

P A P5 3 P5 4 P5 5 C53 0,4 3 0,6 2

C54 0,4 4 0,6 C55 0,4 5 0,317.

Обчислюємо np p 5 0,4 0,4 2 , тому найбільш імовірне число влучень у мішень буде m0 np p 2 .

Задача 1.12. У результаті проведення досліду подія А відбувається з імовірністю p = 0,001. Дослід проводиться 2000 разів. Яка ймовірність того, що подія А відбудеться не менше двох і не більше чотирьох разів?

Розв’язання. За умовою n = 2000, p = 0,001, тому краще використовувати формулу (1.6). Обчислимо a np 2 , тоді

P( А) P

(2) P

(3) P

(4)

22

e 2

23

e 2

24

e 2

0,541.

n

n

n

2!

3!

4!

Задачі

Група А

1.64.Радіолокаційна станція виявляє ціль з імовірністю, яка дорівнює 0,4. Яка ймовірність того, що ціль буде виявлена двома РЛС із чотирьох?

1.65.Прилад складається з 10 вузлів. Надійність (імовірність безвідмовної роботи) кожного вузла протягом часу T дорівнює 0,9. Вузли виходять з ладу незалежно один від одного. Знайти ймовірності того, що за час T: 1) вийде з ладу принаймні один вузол; 2) вийде з ладу один вузол; 3) вийдуть з ладу два вузли;

4)вийдуть з ладу не менше двох вузлів.

1.66.Проводять дев’ять незалежних випробувань, у кожному з яких імовірність появи події А дорівнює 0,4. Знайти найбільш імовірне число появ події А та відповідну ймовірність.

1.67.Апаратура складається з 10 000 елементів, кожний з

яких може незалежно вийти з ладу за час T з імовірністю 5 10 4 . Знайти ймовірності подій: 1) за час T вийде з ладу принаймні один елемент; 2) вийдуть з ладу три елементи; 3) вийдуть з ладу не більше трьох елементів.

1.68. Група з п’яти літаків бомбардує військовий об’єкт, причому кожний з літаків скидає по одній бомбі. Імовірність того,

що бомба влучить у об’єкт, дорівнює 13 . Для знищення об’єкта

потрібно не менше трьох влучень. Знайти ймовірність того, що об’єкт буде знищено. Яке число влучень буде найбільш імовірним?

1.69. Імовірність влучити у мішень при одному пострілі дорівнює 0,25. Стрілець зробив п’ять пострілів. Знайти ймовірності подій: A = {принаймні одне влучення}; B = {одне влучення}; C = ={два влучення}; D = {не менше трьох влучень}; E = {число влучень не менше чотирьох і не більше двох}.

1.70. Прилад дає від’ємні помилки з імовірністю 1 і додатні

3

– з імовірністю 23 . Знайти найбільш імовірне число від’ємних та

додатних помилок при чотирьох вимірюваннях та ймовірність найбільш імовірного числа від’ємних помилок.

Група Б

1.71. Два рівносильних шахісти домовилися зіграти турнір з 2п результативних партій. Нічиї не враховуються і вважається, що кожний з учасників може виграти чергову партію з імовірністю, яка дорівнює 0,5. Переможцем вважається той, хто виграв більше партій. В якому турнірі більше шансів виграти будь-якому з учасників: 1) у турнірі з восьми результативних партій; 2) у турнірі

з12 результативних партій?

1.72.Підводний човен атакує корабель і випускає по ньому

послідовно та незалежно n торпед, які влучають у корабель з імовірністю p . Кожна торпеда, що влучить у корабель з

однаковою ймовірністю, влучає в будь-який з R відсіків, на які розділена підводна частина корабля. Торпеда, що влучила у відсік, призводить до затоплення його водою. Корабель починає тонути, якщо водою заповнено не менше ніж два відсіки. Яка ймовірність того, що корабель буде потоплено?

1.73.За один цикл автомат виробляє 10 деталей. Імовірність того, що деталь бракована, дорівнює 0,01. Скільки потрібно циклів, щоб з імовірністю, яка більше за 0,8, відбулася подія А={принаймні одна деталь бракована}?

1.74.Прилад складається з n вузлів. Надійність роботи j-го

вузла дорівнює p j , j=1,2,…, n. Для роботи приладу потрібна

безвідмовна робота всіх його вузлів. При обчисленні ймовірності відмови приладу P ймовірності p j , j=1, 2,…, n наближено

1 n

замінюють середнім арифметичним p j . Чи буде приблизно

n j 1

~

обчислене значення ймовірності відмови приладу P більше Р? 1.75. Щоб закурити громадянин діставав навмання одну з

двох коробок сірників. Через деякий час він виявив, що одна коробка порожня. Яка ймовірність того, що в другій коробці залишилось k (k n) сірників, якщо спочатку в кожній коробці

було по п сірників? (Задача Банаха).

{ , f , P}

1.76.Велика партія виробів має один відсоток браку. Яким має бути об’єм випадкової вибірки, щоб імовірність події А ={у партії є принаймні один бракований виріб} була більша за 0,95?

1.77.Послідовно посилають чотири радіосигнали. Імовірність приймання кожного з них не залежить від того, прийняті інші сигнали чи ні, та відповідно дорівнює 0,1; 0,2; 0,3; 0,4. Знайти ймовірність приймання k сигналів (k = 0, 1, 2, 3, 4).

1.78.За умовами задачі 1.77 обчислити ймовірність встановлення двобічного радіозв’язку, якщо ймовірність цієї події при прийманні одного сигналу дорівнює 0,2, при прийманні двох сигналів – 0,6, а при прийманні трьох або чотирьох сигналів – 1.

ГЛАВА 2. ВИПАДКОВІ ВЕЛИЧИНИ

2.1. Дискретні випадкові величини, їхні закони розподілу та числові характеристики

Випадкова величина – це змінна величина, можливі значення якої залежать від результату стохастичного експерименту. Запровадимо математичне означення. Нехай –

ймовірнісний простір. Функція ( ) , яка визначена на просторі, має значення у множині дійсних чисел R і для x R – подія

: ( ) x f , називається випадковою величиною. Якщо (

) набуває тільки скінченну або зчисленну множину значень, то вона називається дискретною випадковою величиною.

Законом розподілу будь-якої дискретної випадкової величини називається співвідношення, яке визначає залежність між значеннями випадкової величини та ймовірностями, з якими ці значення набуваються.

Закон розподілу дискретної випадкової величини найчастіше задається рядом розподілу (табл. 2.1).

				Таблиця 2.1
( )	x1	x2	. . .		xn
р	p1	p2	. . .		pn