Теор.вер

У табл. 2.1: pk P : xk , k = 1,2,..., n.

Універсальною характеристикою будь-якої випадкової величини є функція розподілу, яка за означенням дорівнює:

F (x) P{ : () x}.

Основні властивості функції розподілу:

1) функція розподілу є неспадною функцію з областю значень 0, 1 ;

2) є неперервною зліва, тобто lim F x F x0 ;
3) lim F x 0,	x x0	0
	lim F (x) 1;
x	x
4) P a b F b F a .

Для дискретної випадкової величини F x P xk . Це

xk x

завжди розривна функція, яка має зчисленне або скінченне число стрибків у точках можливих значень випадкової величини .

Значення кожного стрибка дорівнює pk .

До найважливіших числових характеристик випадкових величин належать математичне сподівання (ймовірнісне середнє) та дисперсія. Математичне сподівання відповідає середньому значенню випадкової величини і для дискретної випадкової величини обчислюється за формулою

M xk P{ xk } .	(2.1)

k 1

Ряд має збігатися абсолютно, в іншому разі кажуть, що випадкова величина не має математичного сподівання.

Основні властивості математичного сподівання:

1)MC=C, де C – будь-яка стала;

2)M (C ) CM ;

3)M ( ) M M ;

4)випадкові величини та називаються незалежними, якщо для будь-яких x та y події : () x та : () y є

незалежними. Якщо та – незалежні випадкові величини, то

M M M .

Дисперсія характеризує розсіювання випадкової величини навколо математичного сподівання. Дисперсія задається формулою

D M ( M )2 .

(2.2)

Для дискретної випадкової величини дисперсію обчислюємо

так:

D (xk M )2 P{ xk } .	(2.3)

k 1

Основні властивості дисперсії, які випливають з (2.2): 1) DC = 0, де C – будь-яка стала;

2) D(C ) C 2 D ;

3) D M 2 (M )2 .

Останню властивість часто використовують для обчислення дисперсії, для дискретної випадкової величини вона набуває вигляду:

D xk	2 P{ xk } (M )2 ;	(2.4)

k1

4)якщо та – незалежні випадкові величини, то

D( ) D D .

Розмірність дисперсії не збігається з розмірністю випадкової величини. Для того, щоб розмірність характеристики розсіювання була така сама, як розмірність випадкової величини, вводять

середньоквадратичне відхилення (стандартне відхилення)

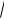D .

Для знаходження числових характеристик дискретної випадкової величини, яка набуває цілих значень, можна використовувати генератрису:

	Ф (z) P{ xk }zk .		(2.5)
	k 1
Тоді
M Ф (1)	; D Ф (1) Ф (1) [Ф (1)]2 .

Приклади розв’язання задач

Задача 2.1. Три рази стріляють по мішені. Імовірність влучення при кожному пострілі дорівнює 0,3. Нехай випадкова величина означає кількість влучень при трьох пострілах. Треба:

1)скласти ряд розподілу випадкової величини ;

2)записати і побудувати графік функції розподілу;

3)обчислити математичне сподівання M і дисперсію D ;

4)знайти ймовірність події А ={кількість влучень буде не

менше двох}.

Розв’язання.

1. При складанні ряду розподілу необхідно знати значення та ймовірності p, з якими ці значення набуваються. За умовою задачі може набувати чотирьох значень: x1 = 0, x2 = 1, x3 = 2, x4

= 3. Імовірності, з якими ці значення набуваються, знайдемо за формулою Бернуллі:

P{ k} Ck pk (1 p)3 k , де k = 0, 1, 2, 3;							p = 0,3.
		3
Отже, ряд		розподілу		випадкової величини має вигляд
(табл.2.2):
					Таблиця 2.2
		0		1	2		3
	p	0,343		0,441	0,189		0,027
2. Записуємо функцію розподілу, користуючись рядом
розподілу:
				0,	x 0;
				0,343,	0 x 1;
		F (x) = 0,784,			1 x 2;
				0,973,	2 x 3;
				1,	x 3.

Графік функції розподілу наведений на рис. 2.1. y

1

0

1

2

3

x

Рис. 2.1

3. Обчислимо математичне сподівання та дисперсію за формулами (2.1) та (2.4):

M 0·0,343+1·0,441+2·0,189+3·0,027=0,9;

D 0 0,343 1 0,441 4 0,189 9 0,027 0,9 2 0,63.

4. Імовірність події А знайдемо так:

P(A) P{ 2} 1 P{ 2} 1 F (2) 1 0,784 0,216.

Задача 2.2. Перевіряють деталі в режимі перевантаження. Імовірність пройти випробування для кожної деталі дорівнює 0,8. Випробування незалежні одне від одного і закінчуються одразу, як тільки деталь, яку перевіряють, виходить з ладу. Скласти ряд розподілу випадкової величини , яка задає кількість випробувань.

Обчислити математичне сподівання M і дисперсію D . Розв’язання. Дискретна випадкова величина може

набувати нескінченної кількості значень: x1=1, x2 =2, ..., xk = k, ...

Для знаходження ймовірностей, з якими ці значення набуваються, будемо використовувати теорему множення ймовірностей для незалежних подій. Отже, загальна формула визначення відповідних імовірностей буде такою:

	P{ k} (1 p)k 1 p , де р = 0,2,						k = 1, 2, ... .
Таким чином, ряд розподілу						має вигляд (табл.2.3):
							Таблиця 2.3
		1	2	...		k		...
	р	0,2	0,16	...		(0,8)k 1 0,2		...

Числові характеристики випадкової величини обчислимо за допомогою генератриси (2.5):

pz

Ф (z) P{ k}z k

q k 1 pzk

, де q =1 – p,

1 qz

k 1

k 1

Тоді

M Ф

(1)

1

1

5 ;

p

0,2

D Ф (1) Ф (1) [Ф

(1)]2

q

20.

p2

Розподіл, який має ця випадкова величина, називається

геометричним.

Задачі

Група А

2.1. Проводять один дослід, у результаті якого подія А може відбутися з імовірністю р. Нехай – індикаторна випадкова

величина, тобто дорівнює одиниці, якщо подія А відбулася, та нулю – якщо не відбулася. Скласти ряд розподілу випадкової величини , записати функцію розподілу, обчислити числові

характеристики. При якому значенні ймовірності р дисперсія набуває максимального значення?

2.2.Розглядаючи стале число а як окремий випадок випадкової величини, знайти: 1) ряд розподілу числа а; 2) функцію розподілу а; 3) числові характеристики.

2.3.1. До випадкової величини додали сталу величину.

2.Випадкову величину помножили на сталу величину. Як

змінилися її числові характеристики в обох випадках?

2.4. Зенітний підрозділ відкриває вогонь по ланці бомбардувальників, яка складається з трьох літаків. Імовірність влучення у перший літак дорівнює 0,2; у другий – 0,5; у третій – 0,3. Скласти ряд розподілу випадкової величини – кількості

збитих літаків, знайти функцію розподілу та обчислити числові характеристики. Знайти ймовірності подій: А = { <2}; В = { 1 }.

2.5. У приладі працюють незалежно один від одного два блоки. Надійність (імовірність безвідмовної роботи за деякий час) першого блока дорівнює 0,8; другого – 0,6. Нехай – випадкова

величина, яка означає кількість блоків, що працюють протягом заданого часу. Скласти ряд розподілу величини , знайти функцію

розподілу та обчислити числові характеристики. Розв’язати аналогічну задачу для випадкової величини , яка означає

кількість блоків, що відмовили.

2.6. У шухляді є чотири лампи, які працюють, та одна лампа, що не працює. Навмання беруть одночасно три лампи. Скласти ряд розподілу випадкової величини , яка означає кількість ламп, що

працюють, серед трьох вийнятих. Записати функцію розподілу величини та обчислити числові характеристики.

2.7. Чотири РЛС незалежно одна від одної виявляють цілі. Імовірність виявлення цілі першою станцією дорівнює 0,4, другою

– 0,6, третьою та четвертою – 0,5. Випадкова величина означає

кількість станцій, які виявили ціль. Записати функцію розподілу величини . Знайти числові характеристики та ймовірність події

А={2 4} .

2.8. Є сім радіоламп, з яких три не працюють, але вони не відрізняються від нових. Навмання беруть чотири радіолампи. Випадкова величина означає кількість ламп, які працюють, серед

узятих. Записати функцію розподілу величини та знайти числові характеристики.

Група Б

2.9. З урни, в якій є п’ять білих та три чорні кулі, послідовно виймають кулі до появи білої. Скласти ряд розподілу кількості чорних куль серед узятих, обчислити математичне сподівання та дисперсію:

1)якщо вийняті кулі в урну не повертають;

2)якщо вийняті кулі повертають в урну.

2.10.Виконують ряд спроб запустити двигун. Кожна спроба

закінчується запуском двигуна незалежно від інших спроб з імовірністю, яка дорівнює 0,6 і займає час . Знайти закон розподілу загального часу Т, який потрібен, щоб запустити двигун, його математичне сподівання та дисперсію.

2.11.Проводять випробування п’яти приладів на надійність. Кожний наступний прилад випробовують тільки тоді, коли попередній виявиться ненадійним. Скласти ряд розподілу та знайти математичне сподівання кількості приладів, які пройшли випробування. Відомо, що ймовірність пройти випробування для кожного приладу дорівнює 0,9.

2.12.Два прилади працюють незалежно один від одного. Кожен прилад має два блоки. Надійність (імовірність безвідмовної

роботи) блоків першого приладу дорівнює 0,7, а надійність блоків другого приладу – 0,4. Випадкова величина означає загальну

кількість блоків, що працюють за період експлуатації приладів. Скласти ряд розподілу та функцію розподілу величини . Знайти

ймовірності подій А={ 1}, В={ <3}, а також числові характеристики випадковоъ величини .

2.13.Сигнали на ввімкнення приладів подаються через кожні 5 с. Час від моменту передачі сигналу до ввімкнення приладу –16 с. Подача сигналів припиняється відразу після того, як ввімкнено принаймні один прилад. Знайти ряд розподілу для випадкового числа поданих сигналів, якщо ймовірність ввімкнення для кожного приладу дорівнює 0,5.

2.14.При передачі повідомлення по радіоканалу зв’язку спостерігаються перешкоди, які заважають його декодувати. Повідомлення не вдається декодувати з імовірністю р. Його передають доти, доки його не декодують. Довжина передачі повідомлення дорівнює 2 хв. Знайти математичне сподівання часу Т, що витрачений на передачу повідомлення.

2.15.По каналу зв’язку у двійковому коді передають повідомлення. Знаки “0” або “1” чергуються з рівною ймовірністю незалежно один від одного. Розглядають будь-яку групу знаків, які

повторюються, наприклад, “0”, “0”, “0”, ... або “1”, “1”, “1”, ... .

Беруть навмання одну з таких груп. Випадкова величина задає

кількість знаків у такій групі. Знайти її закон розподілу, числові характеристики, а також імовірність P{ k} .

2.2. Неперервні випадкові величини, їхні закони розподілу та числові характеристики

Випадкова величина називається неперервною, якщо її

функція

розподілу

F (x) P{ x}

є

неперервною,

диференційовною майже скрізь, за винятком можливо окремих ізольованих точок. Решта властивостей функції F (x) для

неперервних випадкових величин такі самі, як і для дискретних випадкових величин. Закон розподілу неперервної випадкової величини найчастіше задається щільністю розподілу

ймовірностей. За означенням щільність розподілу дорівнює границі

			f	(x) lim	Р x x x	.	(2.6)
				x 0	x
Із формули (2.6) випливають основні властивості
щільності розподілу ймовірностей:
1)	f (x) 0,			x R ;
2)	f		(x) F	(x);
3)	f (x)dx 1 (умова нормування);
				b
4)	P{a b} f (x)dx F b F a .

a

(Остання властивість справджується також для відкритих та напіввідкритих проміжків, тому що для неперервної випадкової величини P{ m} 0 , де m – будь-яка стала величина);

x

5) F (x) f (t)dt .

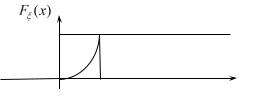
Основні числові характеристики неперервної випадкової величини обчислюють за формулами:

M		xf (x)dx,	(2.7)
за умови, що цей інтеграл збігається абсолютно;
D	(x M )2 f (x)dx		(2.8)
або
D	x2 f (x)dx (M )2.		(2.9)

Зміст цих характеристик такий самий, як і для дискретних випадкових величин.

Приклади розв’язання задач

Задача 2.3. Функція розподілу неперервної випадкової величини має вигляд:

0,			x 0;
	3	,	0 x 1;
F (x) ax
	1,		x 1.

1.Знайти коефіцієнт а та побудувати графік F (x) .

2.Записати щільність розподілу ймовірностей f (x) та

побудувати її графік.
3.	Обчислити математичне сподівання M						і дисперсію D .
			1		3
4.	Знайти ймовірність події					.
			4		4
Розв’язання.
1.	Функція розподілу випадкової величини – неперервна,
тому	lim F (x)	lim F (x) . Звідси а				= 1.	Графік функції
x 1 0		x 1 0

розподілу зображено на рис. 2.2.

1

0

1

x

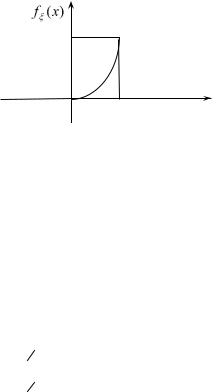
Рис. 2.2

2. Щільність розподілу ймовірностей (2.6) знайдемо за властивістю 2:

	0,			x 0, x 1;
f (x)		2	,	0 x 1.
3x

Графік щільності розподілу наведений на рис. 2.3.

										1
										0				1													x
												Рис. 2.3
3. За формулами (2.7) та (2.9) обчислимо числові
характеристики M						і D :
											1							3					1				3
				M xf (x)dx x 3x 2 dx																x 4								;
											0							4					0				4
										1								3			2				3x		5				1	9			3
	2								2		2		2
D x			f (x)dx				(M )			= x				dx
												3x																										.
										0								4							5						0	16			80
4. Імовірність відповідної події знайдемо за властивістю 4
щільності розподілу ймовірностей:
1					3		34							3							1
							f
P										(x)dx F							F								0,4062.
					4
4							1	4						4							4
Задача 2.4. Випадкова величина																	розподілена за законом