Лекція 4. "Покажчики і Рекурсія"

• адресна арифметика мови Сі

• покажчики, основні поняття

• покажчики і масиви

• особливості масивів великих розмірів

• що таке рекурсія

• рекурсивний пошук

• переваги і недоліки рекурсій

• коли рекурсія не потрібна

• застосування функцій для декомпозиції завдання

12. Рекурсія

Функція називається рекурсивної, якщо під година її обробки виникає її повторний виклик, або безпосередньо, або побічно, шляхом ланцюжка викликів інших функцій.

Прямою (безпосередньої) рекурсією є виклик функції усередині тіла цієї функції.

іnt a()

{.....a()....}

Непрямою рекурсією є рекурсія, що здійснює рекурсивний виклик функції за допомогою ланцюжка виклику інших функцій. Всі функції, що входять у ланцюжок, теж уважаються рекурсивними.

Наприклад:

a(){....b()....}

b(){....c()....}

c(){....a()....} .

Всі функції a, b, c є рекурсивними, тому що при виклику однієї з них, здійснюється виклик інших і самої собі.

Розглянемо завдання про Ханойські вежі.

7. Ханойські вежі (рекурсивні алгоритми)

Одна з улюблених дитячих іграшок - пірамідка з кольоровими кільцями різного діаметру, насадженими на стержень.

Проте є країни, де в цю гру грають шановані і поважні старики. Придумали її ченці древнього Ханоя (тепер це територія В'єтнаму). У них була одна повна пірамідка з 64 кільцями і два порожні стержні. Вважалося, що коли усі кільця вдасться перенести на інший стержень, дотримуючи усі правила (див. нижче), настане кінець світу.

1. Правила гри

Вимагається перенести пірамідку з одного стержня на інший, використовуючи третій стержень як проміжного і дотримуючи наступні правила:

• за одну дію можна переносити тільки одне кільце;

• кільце можна укладати або на вільний стержень, або на більше кільце.

Вирішимо спочатку найпростіше завдання - для пірамідки з двох кілець.

Позначимо стержні номерами:

1 лівий стержень, на якому знаходиться пірамідка на початку гри

2 середній стержень, допоміжний

3 правий стержень, на нього потрібно перенести пірамідку

Позначатимемо ходи стрілками. Біля основи стрілки писатимемо номер початкового стержня, з якого беремо кільце, а у вістря - номер стержня, на який його переносимо.

Ханой-2 {

/* переносемо одне кільце на другий стержень */

1 2;

/* переносемо нижнє кільце на третій стержень */

1 3;

/* переносемо три кільця з другого на третій */

2 3;

}

Ханой-2 (nach, kon, vspom){

nachvspom;

nachkon;

vspomkon;

}

Трохи складніше вирішити завдання для пірамідки з трьох кілець. Зверніть увагу, що нижнє кільце можна класти тільки на порожній стержень. А для цього нам потрібно верхні два кільця перекласти на середній стержень, скориставшись алгоритмом Ханой-2. Потім переносимо велике кільце на третій стержень і, знову використовуючи алгоритм Ханой-2, переносимо два менші кільця на третій стержень.

Ханой-3 {

/* переносим два кільца */

/* на другий стержень */

//1  3; 1  2; 3  2;

Ханой-2 (1,2,3);

/* переносимо велике кільце */

/* на третій стержень */

1  3;

/* переносимо два маленьких кільця */

/* з другого на третій */

//2  1; 2  3; 1  3;

Ханой-2 (2,3,1);

}

У цьому алгоритмі ми двічі використовували алгоритм Ханой-2, але при цьому різні стержні виступали кінцевим і допоміжним.

Ханой-4 {

/* переносимо три кільця на другий стержень */

Ханой-3 (1,2,3);

/* переносимо нижнє кільце на третій стержень */

1  3;

/* переносимо три кільця з другого на третій */

Ханой-3 (2,3,1);

}

Загальний алгоритм для n кілець.

1. Переносимо n - 1 кілець на другий стержень

2. Переносимо нижнє кільце на третій стержень

3.Переносимо n - 1 кілець з другого на третій

Рішення для піраміди з n кілець можна записати у такому вигляді:

Ханой ( n, nach, kon, vspom)

{

якщо n > 1, то

Ханой ( n - 1, 1, 2, 3 );

початковий ( кінцевий;

якщо n > 1, то

Ханой ( n - 1, 2, 3, 1 );

}

Тут в якості початкового, кінцевого і допоміжного можна використовувати будь-які стержні. Алгоритм Ханой фактично пропонує вирішувати задачу для n кілець через два завдання для меншого числа кілець (n - 1). Такий прийом в програмуванні називається рекурсія.

1. Що таке рекурсія?

• Рекурсія - спеціальний прийом в програмуванні, коли алгоритм рішення задачі містить алгоритм рішення подібної задачі, але з іншими початковими даними.

Тепер ми познайомилися з четвертим видом алгоритмів - рекурсивним алгоритмом. Помітимо, що для перенесення пірамідки з двох кілець потрібно всього 3 ходи, для трьох кілець - вже 3+1+3=7 ходів, для чотирьох - 15 і так далі. Можна показати, що для перенесення пірамідки з n кілець нам буде потрібно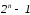ходів. У ченців древнього Ханоя була пірамідка з 64 кілець і вони вірили, що коли вдасться перенести усю пірамідку на третій стержень, настане кінець світу. 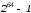Отже, це легенда, але число насправді дуже велике і для того, щоб зробити стільки ходів, не вистачить декількох людських життів.

Рекурсію має сенс використовувати тоді, коли в результаті початкове завдання зводиться до більше за просту. Доведено, що будь-який рекурсивний алгоритм можна замінити алгоритмом без рекурсії (який іноді може бути дуже громіздким). Оскільки використання рекурсії в реальних програмах пов'язане з деякими технічними проблемами, краще її не застосовувати, якщо є простий не рекурсивний алгоритм.

Нижче наведена програма, що вводити число n і друкує список переміщень, що вирішує завдання про Ханойські вежі при кількості дисків n. Використовується внутрішня рекурсивна процедура tn(n, і, j, w), що друкує переміщення, необхідні для перенесенню n дисків зі стрижня й на стрижень j з використанням допоміжного стрижня w при {і, j, w} = {1,3,2}.

/* ханойські вежі */

#include

main() /* що викликає */

{ void tn(int, int, int, int); /* функція */

int n;

scanf(" %d",&n);

tn(n, 1,3,2);

}

void tn(int n, int nach, int kon, int w) /* рекурсивна */

{ if (n>1) /* функція */

{ tn (n - 1, nach, w, kon);

tn (1, nach, kon, w);

tn (n - 1, w, kon, nach);

}

else printf(" %d -> %d", nach, kon);

return ;

}

Послідовність викликів процедури tn при m=3 ілюструється деревоподібною структурою на рис.33. Щораз при виклику процедури tn під параметри n, nach, kon, w виділяється пам'ять і запам'ятовується місце повернення. При поверненні із процедури tn пам'ять, виділене під параметри n, nach, kon, w, звільняється й стає доступної пам'ять, виділена під параметри n, nach, kon, w попереднім викликом, а керування передається в місце повернення.

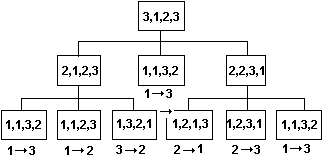
Рис.33. Послідовність викликів процедури tn

У багатьох випадках рекурсивні функції можна замінити на еквівалентні не рекурсивні функції або фрагменти, використовуючи стеки для зберігання крапок виклику й допоміжних змінних.

Припустимо, що є ситуація:

main() /* зухвала функція */

{ ... f()...}

f() /* рекурсивна функція */

{ ... f()...}

Тут у функції maіn викликається рекурсивна функція f. Потрібно замінити опис функції f і її виклику на еквівалентний фрагмент програми, тобто видалити функцію f.

Нехай рекурсивна функція f має параметри Р1, Р2,...,Рs, внутрішні змінні V1, V2,...,Vt і у функціях maіn і f є k звертань до функції f. Для видалення такої функції потрібні наступні додаткові об'єкти :

- змінні AR1, AR2,...,ARs, що містять значення фактичних параметрів при виклику функції f (типи змінних повинні відповідати типам параметрів Р1, Р2,...,Рs);

- змінна rz для результату, що обчислюється функцією f (тип змінних збігається з типом значення функції, що повертається, f);

- стік, що містить у собі всі параметри й всі внутрішні змінні функції f, а також змінну lr типу іnt, для зберігання крапки повернення, і змінну pst типу покажчик, для зберігання адреси попереднього елемента стека;

- покажчик dl для зберігання адреси вершин стека;

- проміжний покажчик u для операцій над стеком;

- k нових міток L1,...,Lk для позначених крапок повернення;

- мітка jf, використовувана для обходу модифікованого тіла функції f;

- проміжна змінна l типу іnt для передачі номера крапки повернення.

Щоб одержати еквівалентну не рекурсивну програму без функції f, необхідно виконати наступні дії:

1. Забрати оголошення функції f у функцію maіn;

2. Додати у функції maіn оголошення змінних AR1, AR2,...,ARs, RZ, оголошення стека ST і покажчиків dl і u:

typedef struct st { P1;P2;...;Ps;V1;V2;...;Vt;

int lr; struct st *pst } ST;

ST *dl=NULL, *u;

3. Модифікувати тіло функції f у фрагмент програми. Для цього треба:

а) видалити заголовок функції f;

б) оголошення параметрів і внутрішні змінних і замінити фрагментом:

goto jf;

f: a=malloc(sizeof(ST));

a ->P1=AR1; a ->P2=AR2; ... ;a ->Ps=ARs;

a ->lr=l; a ->pst=dl; dl=a;

в) наприкінці функції f поставити мітку JF, а всі звертання до формальних аргументів замінити обігом, до відповідних елементів стека;

г) замість кожного оператора return(y) у функції f записати фрагмент:

RZ=y; l=dl ->lr;

a=dl; dl=a ->pst; free(a);

switch(l)

{ case 1: goto L1;

case 2: goto L2;

...

case k: goto Lk;

}

4. Кожний і виклик функції f (як у зухвалій функції, так і в тілі функції f) виду V=f(A1, A2,...,As) замінити фрагментом програми :

AR1=A1; AR2=A2; ... ; ARs=As; l=i; goto f;

Li: V=RZ;

де l=і позначає l=1 при першому звертанні до функції f, l=2 при іншому обігу й т.д. Нумерація обігів може бути виконана в довільному порядку й потрібно для повернення в крапку виклику за допомогою операторів swіtch і goto Lі; (де Lі є L1 при першій заміні, Lі є L2 при другій заміні й т.д.)

5. Вставити модифіковане тіло функції f наприкінці функції maіn.

Для ілюстрації викладеного розглянемо кілька варіантів реалізації програми що обчислює функцію Акермана, що визначається так:

+ X+1, якщо N=0

| X, якщо N=1, Y=0

| 0, якщо N=2, Y=0

A(N, X, Y)= | 1, якщо N=3, Y=0

| 2, якщо N=>4, Y=0

+ A(N - 1, A(N, X, Y - 1), X), якщо N#0, Y#0;

де N, X, Y - цілі ненегативні числа.

Наступна програма обчислює функцію Акермана з використанням рекурсивної функції ackr і допоміжної функції smacc:

/* рекурсивне обчислення функції Аккермана */

# include

main () /* що викликає */

{ int x, y, n, t; /* функція */

int ackr(int, int, int);

scanf("%d %d %d",&n,&x,&y);

t=ackr(n, x, y);

printf("%d", t);

}

int smacc( int n, int x ) /* допоміжна */

{ switch (n) /* функція */

{ case 0: return(x+1);

case 1: return (x);

case 2: return (0);

case 3: return (1);

default: return (2);

}

}

int ackr( int n, int x, int y) /* рекурсивна */

{ int z; /* функція */

int smacc( int, int);

if(n==0 || y==0) z=smacc(n, x);

else { z=ackr(n, x, y - 1); /* рекурсивних */

z=ackr(n - 1, z, x); } /* викликів ackr(...) */

return z;

}

Модифікуючи функції maіn і ackr відповідно до викладеного методу одержимо наступну програму:

/* Еквівалентна не рекурсивна програма */

/* для обчислення функції Аккермана */

#include

#include

int main()

{ typedef struct st

{ int i, j, k, z, lr;

struct st *pst;

} ST;

ST *u, *dl=NULL;

int l, x, y, n;

int smacc(int, int);

int an, ax, ay, rz, t;

scanf("%i %i %i",&n,&x,&y);

an=n;ax=x;ay=y;l=1; /* - заміна виклику - */

goto ackr; /* t=ackr(n, x, y); */

l1: t=rz; /* - - - - - - - - */

printf("%d ", t);

goto jackr;

/* початок фрагмента замінюючого функцію ackr */

ackr:

u=( ST *) malloc( sizeof (ST));

u ->i=an;

u ->j=ax;

u ->k=ay;

u ->lr=l;

u ->pst=dl;

dl=u;

if (an==0||ay==0)

dl ->z=smacc(an, ax);

else

{

an=dl ->i; /* - заміна виклику - */

ax=dl ->j; /* */

ay=dl ->k - 1; /* z=ackr(n, x, y - 1); */

l=2; /* */

goto ackr; /* */

l2: dl ->z=rz; /* - - - - - - - - */

an=dl ->i - 1; /* - заміна виклику - */

ax=rz; /* */

ay=dl ->j; /* z=ackr(n - 1, z, x); */

l=3; /* */

goto ackr; /* */

l3: dl ->z=rz; /* - - - - - - - - */

}

rz=dl ->z; /* - - - - - - - - */

an=dl ->i; /* */

ax=dl ->j; /* заміна */

ay=dl ->k; /* */

l=dl ->lr; /* оператора */

u=dl; /* */

dl=u ->pst; /* return z ; */

free(u); /* */

switch(l) /* */

{ case 1: goto l1; /* */

case 2: goto l2; /* */

case 3: goto l3; /* */

} /* - - - - - - - - */

jackr:

}

int smacc( int n, int x ) /* допоміжна функція */

{ switch (n)

{ case 0: return(x+1);

case 1: return (x);

case 2: return (0);

case 3: return (1);

default: return (2);

}

}