Математика

Пример

Решим предыдущую систему матричным методом.

Решение

	x			3
Матрица	1		, матрица			. Выпишем матри-
	X = x2			B = 11
	x3			8

цу А и найдем обратную к ней.

		1								−1								1
A =			2								1 1 . Определитель этой матрицы																																													= 5 .
		1									1						2
Вычислим алгебраические дополнения элементов aij .
A		=				1					1				=1; A						= −			2			1				= –3;						A			=			2						1		=1;
11						1					2								12					1			2										13						1						1
A		= −								−11							=3;			A		=				1	1						=1; A						= −									1 −1							= –2;
21									1		2										22					1	2										23											1	1
A		=					−11						= –2;							A		= −						1			1				=1;		A			=							1 −1								=3.
31							1				1										32							2			1						33										2		1
Обратная матрица будет иметь вид
			1							1								3		− 2
A	−1
		=									−3							1			1	. Тогда
			5
																	− 2
										1											3
																		1	1					3 −								2				3				1				20												4
X = А							−1			В =
																		5	−3 1 1															11				=						10 = 2													.
																																								5
																					− 2						3
																			1																	8								5												1
Отсюда											x 0						= 4,				x	0 = 2,											x 0			=1 (этот ответ совпадает
											1										2												3

с ответом, полученным по формулам Крамера).

11

4. Векторная алгебра

Вектором a называется направленный отрезок прямой. Если точка А – начало вектора, точка В – его конец, то

вектор a может обозначаться AB = a . Длиной или модулем

вектора AB называется число, равное длине отрезка АВ. Рассматривают также вектор, у которого начало и конец

совпадают. Его называют нуль-вектором и обозначают 0 . Нуль-вектор не имеет определенного направления, и его модуль равен нулю.

Векторы a и b , расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Два

вектора a и b называются равными, если они: 1)имеют равные модули; 2) коллинеарны; 3) направлены в одну сто-

рону. Три вектора a, b, c , параллельные одной плоскости

или лежащие в одной плоскости, называются компланарны-

ми.

Произведением вектора a на число λ называется вектор b = λa , имеющий длину b = λ a , направление кото-

рого совпадает с направлением вектора a , если λ > 0 , и противоположно ему, если λ < 0 . При λ = 0 получаем нуль-вектор.

Рассмотрим в пространстве прямоугольную систему координат OXYZ. Отнесем к каждой из осей единичные

векторы i, j,k так, что их направления будут совпадать с положительным направлением соответствующей оси. Единичные векторыi, j,k называются базисными векторами или базисом. Тогда любой вектор в пространстве может быть задан своими координатами a = {x, y, z}, где х – про-

екция вектора а на ось ОХ, y,z – соответственно на оси OY, 12

OZ. С другой стороны, вектор а может быть представлен в виде линейной комбинации базисных векторов:

a = x i + y j + z k

Над векторами можно производить линейные операции, к которым относятся следующие:

1.Сумма двух векторов a = {x1 , y1 , z1} и b = {x2 , y2 , z2 }

–это вектор c с координатами c = {x1 + x2 , y1 + y2 , z1 + z2 }.

2.Разность двух векторов a −b определяется векто-

ром d с координатами d = {x1 − x2 , y1 − y2 , z1 − z2 }.

3. При умножении вектора на скаляр λ , его координаты умножаются на данное число: λa = {λx1 , λy1 , λz1}.

Длина или модуль вектора a определяется через его координаты формулой a = x 2 + y 2 + z 2 . Возможны и другие действия с векторами. Рассмотрим их.

Скалярным произведением векторов a и b называется число, равное произведению модулей этих векторов на ко-

синус угла между ними: a b = a b cosϕ . Можно показать,

что скалярное произведение векторов через их координаты выражается следующим образом:

a b = x1 x2 + y1 y2 + z1 z2 .

С помощью скалярного произведения можно найти

угол между векторами cosϕ =

a

b

, а также проекцию век-

a

b

a

b

тора на заданное направление

пр a =

. Равенство нулю

b

b

13

скалярного произведения является необходимым и достаточным условием перпендикулярности векторов.

В дальнейшем будем использовать еще один вид произведения: векторное произведение двух векторов. Вектор-

ным произведением двух векторов a и b называется вектор

с, который удовлетворяет трем условиям:

1)модуль с вектора численно равен площади парал-

лелограмма, построенного на векторах a и b , то есть

с= a b sinϕ , где ϕ – угол между векторами a и b ;

2)вектор с перпендикулярен векторам a и b ;

3)вектор с направлен так, что три вектора a, b, c об-

разуют правую тройку. Векторное произведение векторов a

и b будем обозначать символом а×b . Можно показать, что векторное произведение выражается через координаты век-

i j k

торов a и b следующим образом a ×b = x1 y1 z1 , где x2 y2 z2

i, j, k – единичные базисные векторы.

По определению модуль векторного произведения ра-

вен площади параллелограмма	a ×b	= Sпар . Тогда площадь
треугольника, построенного на	векторах a и b , равна

S = 12 a ×b . Необходимым и достаточным условием кол-

линеарности двух векторов является равенство нулю их векторного произведения.

Смешанным произведением трех векторов a, b, c на-

зывается число, равное скалярному произведению вектора

14

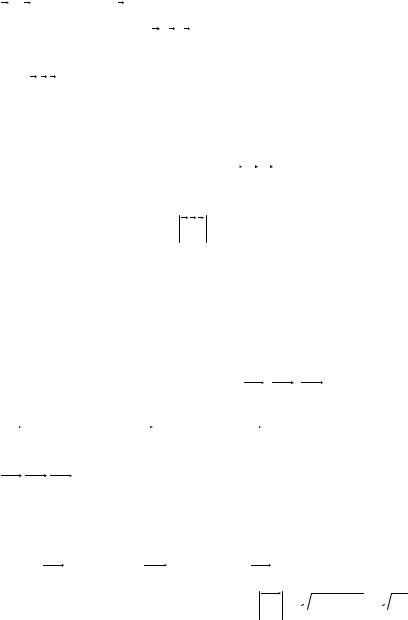
a ×b на вектор c . Формула, выражающая смешанное произведение векторов a, b, c через их координаты, имеет

	x1	y1	z1
вид: a b c =	x2	y2	z2	. Необходимым и достаточным усло-
	x3	y3	z3

вием компланарности трех векторов является равенство нулю их смешанного произведения. Объем параллелепипеда,

построенного на трех векторах a, b, c , равен модулю их смешанного произведения. Объем пирамиды, построенной

на этих векторах, равен 16 abc .

Пример

Даны координаты четырех точек А(1; 2;3), B( 0;-1;1), C(2;5;2), D(3;0;-2). Доказать, что они не лежат в одной плоскости. Найти объем пирамиды АВСD, длины ее ребер, площадь грани АВС, плоский угол ВАС.

Решение

Проверим, лежат ли точки А, В, С, D в одной плоско-

сти. Для этого введем три вектора							АВ, АС, АD и проверим,
компланарны ли они. Найдем							координаты	векторов:
AB = {−1;−3;−2},			AC = {1;3;−1},				AD = {2;−2;−5}.	Тогда
AB AC AD =		−1	−3	− 2		= 24 ≠ 0 .Значит векторы не ком-
		1	3	−1
		2	− 2	−5

планарны, и точки А, В, С, D не лежат в одной плоскости. Найдем координаты других векторов:

BD = {3;1;−3}, DC = {−1;5;4}, BC = {2;6;1}. Длины ре-

бер пирамиды будут равны: AB = 1+9 + 4 = 14 ,

15

AC = 1 +9 +1 = 11 ,		AD = 4 + 4 + 25 = 23 ,
BD =	9 +1 +9 = 19 ,	DC = 1 + 25 +16 = 42 ,
BC =	4 +36 +1 = 41 .

Vпир =				1	24 = 4 .
6
Вычислим площадь грани АВС. Для этого найдем век-
торное произведение векторов АВ, AC :
			i			j	k
AB × AC =			−1 − 3 − 2					= 9i − 3 j .
			1			3	−1
						= 1
Тогда S ABC							92 +32 + 02 = 3 10 .
						2	2
Осталось найти угол ВАС с помощью скалярного про-
изведения тех же векторов:
cosϕ =	AB	AC				= ( −1) 1 +( −3) 3 +( −2 ) ( −1)			== −	8	,
	AB	AC					14 11			154

ϕ= arccos − .

154

5.Уравнения плоскости и прямой

впространстве 8

Пусть в пространстве задана прямоугольная система координат Оxyz. Уравнение F(x,y,z)=0 является уравнением данной поверхности, если координаты каждой точки, лежащей на этой поверхности, удовлетворяют данному уравнению, а координаты любой точки, не лежащей на этой поверхности, – не удовлетворяют. Простейшим видом поверх-

16

ности является плоскость. Рассмотрим различные формы уравнений плоскости.

Пусть в пространстве плоскость (α ) задана точкой М0 (x0 , y0 , z0 ) и вектором n = {A,B,C}, перпендикулярным

плоскости (такой вектор называется нормальным вектором плоскости). Тогда можно записать каноническое уравнение плоскости А(x − x0 ) + B( y − y0 ) +C(z − z0 ) = 0 . Уравнение вида Ax + By +Cz + D = 0 называется общим уравнением.

Уравнение ax + by + cz =1 называется уравнением плоскости

в отрезках. Здесь a – величина отрезка, отсекаемого плоскостью на оси Оx, b – на оси Oy, с – на оси Oz.

Если известны три точки плоскости, не лежащие на

одной прямой, М1 (x1 , y1 , z1 ) , M 2 (x2 , y2 , z2 ) ,				M 3 (x3 , y3 , z3 ) ,
то	из	условия	компланарности	векторов
М1М, М1М2 , М1М3 , где			М( x, y,z )– текущая точка плос-
кости (α ),		можно получить уравнение плоскости, прохо-

дящей через три заданные точки:

x − x1	y − y1	z − z1
x2 − x1	y2 − y1	z2 − z1		= 0
x3 − x1	y3 − y1	z3 − z1

Расстояние от точки M 0 (x0 , y0 , z0 ) до плоскости (α ), заданной общим уравнением, вычисляется по формуле

d = Ax0 + By0 +Cz0 + D .
A2 + B2	+C 2
Прямая линия может быть определена как линия пере-
сечения двух плоскостей A1 x + B1 y +C1 z + D1 = 0		. Удоб-
A2 x + B2 y +C2 z + D2 = 0
нее использовать канонические	уравнения	прямой
		17

	x − x0	=	y − y0	=	z − z0	, где М0( x0 , y0 , z0 ) – точка на пря-
	A		B		C

мой, l = {A,B,C} – направляющий вектор прямой (то есть

вектор, лежащий на прямой или параллельный ей). За направляющий вектор прямой можно взять вектор, равный векторному произведению нормальных векторов плоско-

стей: l = n1 ×n2 .

Уравнение прямой,

проходящей

через

две точки

М1 (x1 , y1 , z1 ) , M 2 (x2 , y2 , z2 ) , можно записать в виде:

x − x1

=

y − y1

=

z − z1

.

x

− x

2

y

2

− y

z

2

− z

1

1

1

Из канонических уравнений прямой можно вывести

параметрические уравнения прямой,

приравнивая каждое

x = At + x0

из отношений параметру t: y = Bt + y0 , где − ∞ < t < +∞.

+ z0

Пример

z = Ct

В системе Oxyz даны точки

А(-1;0;-7),

B( -5;1;-4),

C(-10; 3; 0), D(5; 2; -1). Найти: 1) уравнение плоскости (α ),

проходящей через точки А, В, С;

2) расстояние

от начала

координат до плоскости ; 3) координаты точек пересечения плоскости (α ) с осями координат; 4) cоставить уравнение прямой, перпендикулярной плоскости (α ) и проходящей через точку D; 5) найти проекцию точки D на плоскость (α ) и расстояние от точки D до плоскости (α ); 6) составить уравнение плоскости, проходящей через точку D параллельно плоскости (α ).

18

Решение

1)Уравнение плоскости, проходящей через три точки А,

В, С, будет иметь вид		x +1	y −0	z + 7		= 0 .
		−5 +1	1 −0	− 4 + 7
		−10 +1	3 −0	0 + 7

Раскрывая определитель по элементам первой строки, получим

( x +1)		1 3		− y		− 4	3		+( z + 7 )		− 4	1		= 0 ;
		3 7				− 9	7				− 9	3

или :– 2(x+1)+y–3(z+7)=0; 2x–y+3z+23=0.

Таким образом, уравнение плоскости (α ) имеет вид:

2x–y+3z+23=0.

2) Расстояние от точки О(0,0,0) - начала координат до этой плоскости найдем по формуле

d = 2 0 +( −1) 0 + 3 0 + 23 =

23 .

4 +1 + 9

14

3) Приведем уравнение плоскости (α ) к виду «в от-

резках». Получим

x

+

y

+

z

=1. Тогда точки пере-

23

23

−

23

−

2

3

сечения плоскости (α ) с осями будут иметь координаты: с

				23		(0;23;0), с осью Oz
	осью Ох – М1		−		;0;0 , с осью Oy – М2
				2

–М3 0;0;− 23 .

3

4)Найдем канонические уравнения прямой, проходящей через точку D перпендикулярно плоскости (α ). Из условия перпендикулярности прямой и плоскости следует, что за направляющий вектор прямой можно принять нор-

19

мальный вектор плоскости l = n = {2;−1; 3}. Тогда канонические уравнения прямой будут иметь вид:

	x −5		=	y − 2	=	z +1	.
				−1
2					3
5) Найдем координаты точки D′– проекции точки D
на плоскость (α ).					Параметрические уравнения прямой бу-
дут иметь			вид: x = 5 + 2t; y = 2 −t; z = −1 + 3t . Так как
точка D′		лежит и на проектирующей прямой и на плоско-

сти(α ), то ее координаты должны удовлетворять уравнению плоскости (α ). Подставим значения x, y, z из параметрических уравнений в уравнение плоскости (α ). Получим

2(5+2t)–-(2–t)+3(-1+3t)+23=0.

Откуда найдем t = –2 – значение параметра t, отвечающее точке пересечения прямой и плоскости (α ). Далее найдем координаты проекции точки D на плоскость (α ):

x=5+2(–2)=1;		y=2–(–2)=4;	z = −1 + 3( −2 ) = −7 , то		есть
′
D (1;4;−7) .
Расстояние от точки D до плоскости (α ) найдем по
формуле
d1	= 2 5 +( −1) 2 + 3 ( −1) + 23 = 28 = 2 14 .
		14	14
6) Так как искомая плоскость ( β ) параллельна плос-
кости	(α ),	то нормаль	к плоскости	( β )	равна
nβ = nα	= {2;−1;3}. Тогда уравнение плоскости			( β)	будет
иметь	вид:	2( x −5 ) +( −1)( y − 2 ) + 3( z +1) = 0			или

2x − y + 3z −5 = 0 .

6. Линии второго порядка

Линия второго порядка – это линия, которая в декартовой системе координат задается уравнением второй степени относительно x и y.

20